机器学习-KNN算法
一、算法介绍
KNN算法中文名称叫做K近邻算法,是众多机器学习算法里面最基础入门的算法。它是一个有监督的机器学习算法,既可以用来做分类任务也可以用来做回归任务。KNN算法的核心思想是未标记的样本的类别,由距离他最近的K个邻居投票来决定。下面我们来看个例子加深理解一下:
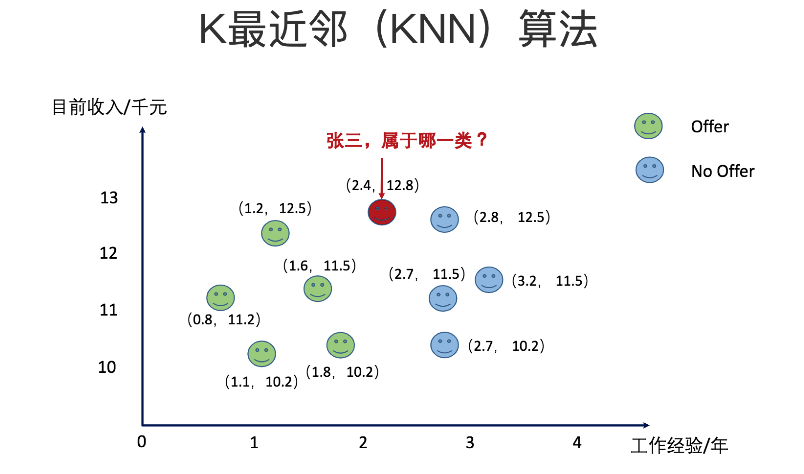
如上图所描述张三要参加一家公司的面试,他通过各种渠道了解到了一些工作年限和工资之间对应的关系以及在这种条件下他们是否获取到了offer的情况。让我们来预测一下张三是否能够拿到他这家公司的offer吧?当K-近邻中的K选择为1的时候我们看下结果。张三不可以拿到offer。
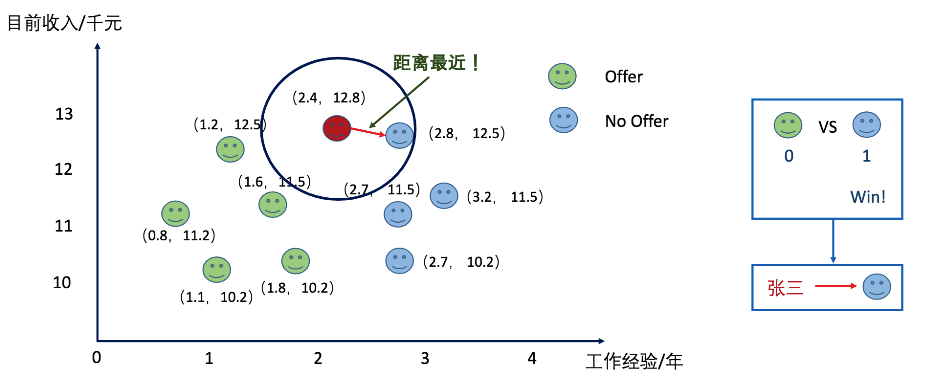
当我们选择K的值为3的时候,张三拿到了offer。
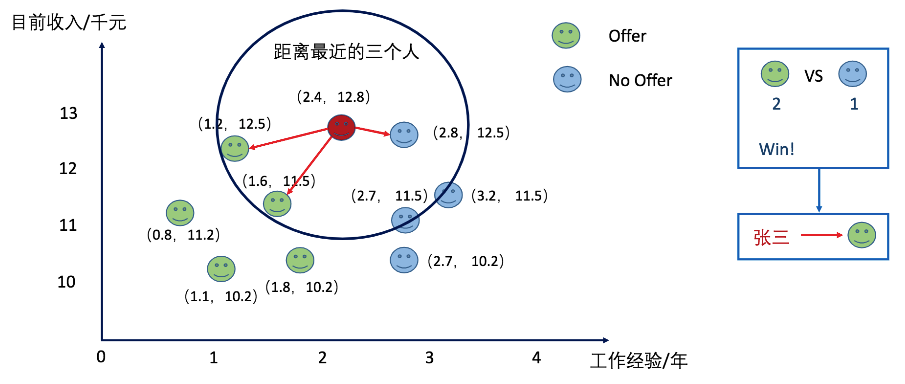
同理当我们选择K的值为5的时候呢?张三被分类到了拿不到offer的类别上了。
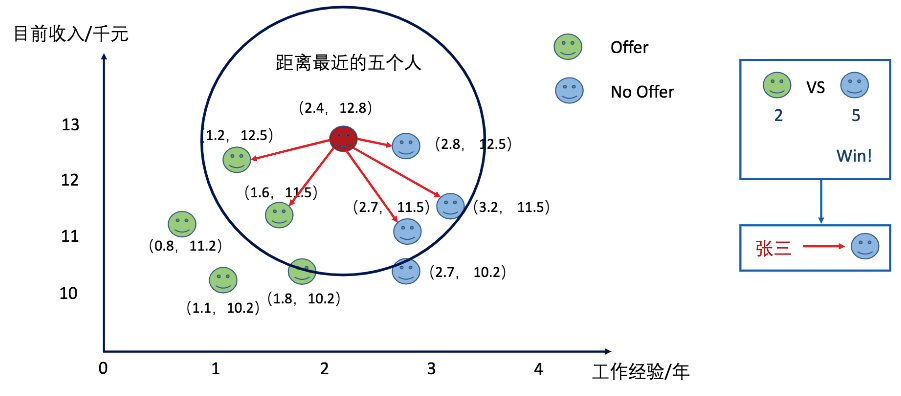
看了上面的例子是不是感觉KNN算法超级的easy。下面我们来稍微深入了解一下算法的实现步骤。
二、算法的实现步骤
假设X_test为待标记的样本,X_train为已标记的样本数据集:
1、遍历X_train中的所有样本,计算每个样本与X_test的之间的距离(一般为欧式距离)。并且把距离保存在一个distince 的数组中。
2、对distince数组进行排序,取距离最近的K个点。记作X_knn。
3、在X_knn中统计每个类别的个数,既class_0在X_knn中有几个样本,class_1在X_knn中有几个样本等。
4、待标记样本的类别就是X_knn中样本个数最多的那个类别。
好了,说完了伪代码以后,我们尝试手写一个KNN的算法吧。
from sklearn import datasets from collections import Counter # 为了做投票 from sklearn.model_selection import train_test_split import numpy as np # 导入iris数据 iris = datasets.load_iris() X = iris.data y = iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=20) def euc_dis(instance1, instance2): """ 计算两个样本instance1和instance2之间的欧式距离 instance1: 第一个样本, array型 instance2: 第二个样本, array型 """ dist = np.sqrt(sum((instance1 - instance2)**2)) return dist def knn_classify(X, y, testInstance, k): """ 给定一个测试数据testInstance, 通过KNN算法来预测它的标签。 X: 训练数据的特征 y: 训练数据的标签 testInstance: 测试数据,这里假定一个测试数据 array型 k: 选择多少个neighbors? """ # TODO 返回testInstance的预测标签 = {0,1,2} distances = [euc_dis(x, testInstance) for x in X] kneighbors = np.argsort(distances)[:k] count = Counter(y[kneighbors]) return count.most_common()[0][0] # 预测结果。 predictions = [knn_classify(X_train, y_train, data, 3) for data in X_test] correct = np.count_nonzero((predictions==y_test)==True) #accuracy_score(y_test, clf.predict(X_test)) print ("Accuracy is: %.3f" %(correct/len(X_test)))
看完了代码的实现以后。我们来思考一下算法的时间复杂度是多少呢?很明显KNN算法的时间复杂度为O(D*N*N)。其中D为维度数,N为样本总数。从时间复杂度上我们可以很清楚的就知道KNN非常不适合高维度的数据集,容易发生维度爆炸的情况。同时我们也发现了一个问题在关于K的选择上面,我们一般也要选择K的值应该尽量选择为奇数,并且不要是分类结果的偶数倍,否则会出现同票的情况。那么说到这里,关于K的选择?我们到底应该怎么去选择K的大小比较合适呢?答案是交叉验证。交叉验证指的是将训练数据集进一步分成训练数据和验证数据,选择在验证数据里面最好的超参数组合。交叉验证或者通俗一点的说法就是说调参。我们不是经常说机器学习或者深度学习工程师为调参工程师嘛。哈哈。调参。参数一般分为模型参数和超级参数。模型参数是需要我们通过不断的调整模型和超参数训练得到的最佳参数。而超参数则是我们人为手动设定的值。像在KNN中超参数就是K的值。我们可以通过交叉验证的方式,选择一组最好的K值作为模型最终的K值。下图是五折交叉验证:

三、实战KNN算法
这里我们使用KNN算法来做最普通的水仙花分类。下面请看代码。超级简单。
# 读取相应的库 from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier import numpy as np # 读取数据 X, y iris = datasets.load_iris() X = iris.data y = iris.target # 把数据分成训练数据和测试数据 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=20) # 构建KNN模型, K值为3、 并做训练 clf = KNeighborsClassifier(n_neighbors=3) clf.fit(X_train, y_train) # 计算准确率 from sklearn.metrics import accuracy_score correct = np.count_nonzero((clf.predict(X_test)==y_test)==True) #accuracy_score(y_test, clf.predict(X_test)) print ("Accuracy is: %.3f" %(correct/len(X_test)))
结果也是达到了 Accuracy is: 0.921
上面说完了KNN用作分类算法以后,我们来看一下KNN算法在做回归算法的时候的表现。KNN用于做回归算法的原理是挑选最近的K个点的值,然后计算这K个点的均值作为回归预测值。下面我们用实战演示一下回归算法。
下面是利用KNN的回归算法来做二手车的价格回归预测的一个小需求例子。
import pandas as pd import matplotlib import matplotlib.pyplot as plt import numpy as np import seaborn as sns #读取数据 df = pd.read_csv('data.csv') df # data frame
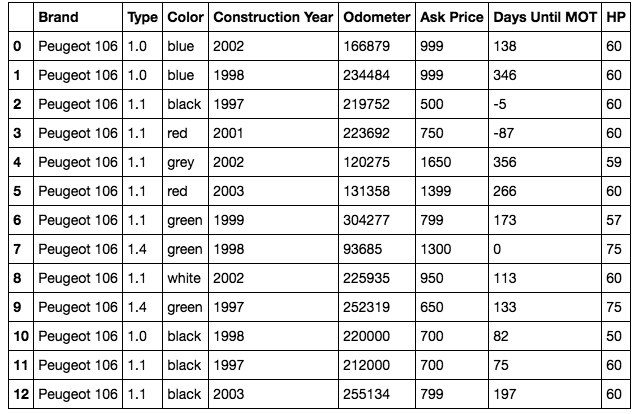
#清洗数据 # 把颜色独热编码 df_colors = df['Color'].str.get_dummies().add_prefix('Color: ') # 把类型独热编码 df_type = df['Type'].apply(str).str.get_dummies().add_prefix('Type: ') # 添加独热编码数据列 df = pd.concat([df, df_colors, df_type], axis=1) # 去除独热编码对应的原始列 df = df.drop(['Brand', 'Type', 'Color'], axis=1) df
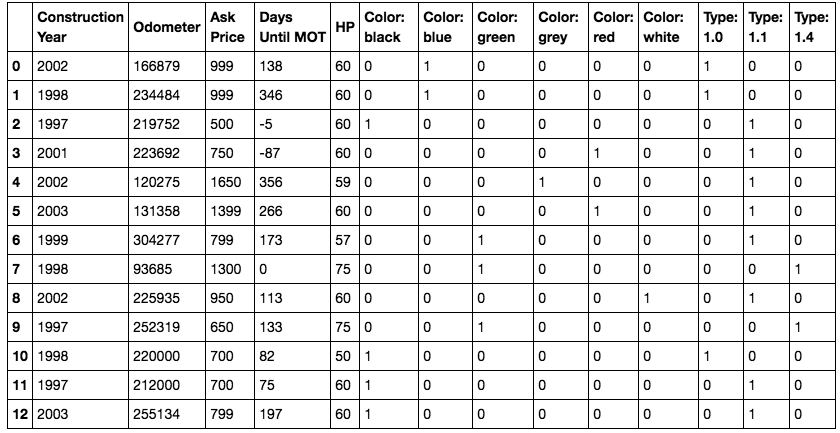
from sklearn.neighbors import KNeighborsRegressor from sklearn.model_selection import train_test_split from sklearn import preprocessing from sklearn.preprocessing import StandardScaler import numpy as np X = df[['Construction Year', 'Days Until MOT', 'Odometer']] y = df['Ask Price'].values.reshape(-1, 1) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=41) X_normalizer = StandardScaler() # N(0,1) X_train = X_normalizer.fit_transform(X_train) X_test = X_normalizer.transform(X_test) y_normalizer = StandardScaler() y_train = y_normalizer.fit_transform(y_train) y_test = y_normalizer.transform(y_test) knn = KNeighborsRegressor(n_neighbors=2) knn.fit(X_train, y_train.ravel()) #Now we can predict prices: y_pred = knn.predict(X_test) y_pred_inv = y_normalizer.inverse_transform(y_pred) y_test_inv = y_normalizer.inverse_transform(y_test) # Build a plot plt.scatter(y_pred_inv, y_test_inv) plt.xlabel('Prediction') plt.ylabel('Real value') # Now add the perfect prediction line diagonal = np.linspace(500, 1500, 100) plt.plot(diagonal, diagonal, '-r') plt.xlabel('Predicted ask price') plt.ylabel('Ask price') plt.show() print(y_pred_inv)
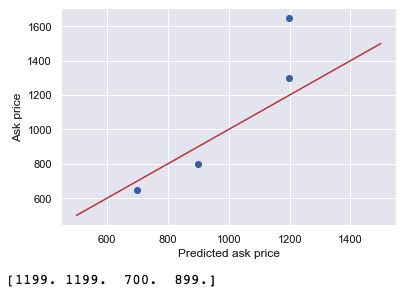
四、KNN需要注意的几个问题
1、大数吞小数
在进行距离计算的时候,有时候某个特征的数值会特别的大,那么计算欧式距离的时候,其他的特征的值的影响就会非常的小被大数给覆盖掉了。所以我们很有必要进行特征的标准化或者叫做特征的归一化。
2、如何处理大数据量
一旦特征或者样本的数目特别的多,KNN的时间复杂度将会非常的高。解决方法是利用KD-Tree这种方式解决时间复杂度的问题,利用KD树可以将时间复杂度降到O(logD*N*N)。D是维度数,N是样本数。但是这样维度很多的话那么时间复杂度还是非常的高,所以可以利用类似哈希算法解决高维空间问题,只不过该算法得到的解是近似解,不是完全解。会损失精确率。
3、怎么处理样本的重要性
利用权重值。我们在计算距离的时候可以针对不同的邻居使用不同的权重值,比如距离越近的邻居我们使用的权重值偏大,这个可以指定算法的weights参数来设置。
五、总结
KNN是一个比较简单的算法,它适合在低维度空间中使用,数据量太大预测时间高,所以需要对大数据量进行一定的处理。
下面给出两篇KD-Tree的文章
https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/kdtrees.pdf
https://zhuanlan.zhihu.com/p/23966698


 浙公网安备 33010602011771号
浙公网安备 33010602011771号