Codeforces Round #370 (Div. 2)（简单逻辑，比较水）

C. Memory and De-Evolution
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Memory is now interested in the de-evolution of objects, specifically triangles. He starts with an equilateral triangle of side length x, and he wishes to perform operations to obtain an equilateral triangle of side length y.

In a single second, he can modify the length of a single side of the current triangle such that it remains a non-degenerate triangle (triangle of positive area). At any moment of time, the length of each side should be integer.

What is the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y?

Input

The first and only line contains two integers x and y (3 ≤ y < x ≤ 100 000) — the starting and ending equilateral triangle side lengths respectively.

Output

Print a single integer — the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y if he starts with the equilateral triangle of side length x.

Examples
Input
6 3
Output
4
Input
8 5
Output
3
Input
22 4
Output
6
Note

In the first sample test, Memory starts with an equilateral triangle of side length 6 and wants one of side length 3. Denote a triangle with sides a, b, and c as (a, b, c). Then, Memory can do .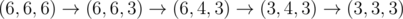

In the second sample test, Memory can do .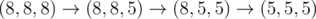

In the third sample test, Memory can do: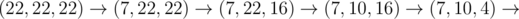

.

 

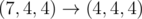题意：

给出边长为x的等边三角形，每次操作可以将其中一边变成任意长度，但改变后三边仍能构成三角形，问最少几次操作可以变成边长为y的等边三角形；

 

思路：

从y往x反推，用数组a存储当前边的状态，每次让最小边变成最长边，由公理：三角形的最长边小于另两边之和得a[0]=a[1]+a[2]-1；

注意边界条件x, 即a[0]=min(a[1]+a[2]-1, x)；

 

代码：

 1 #include <bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 
 5 int main(void)
 6 {
 7     int x, y;
 8     ll ans=0;
 9     cin >> x >> y;
10     int a[3];
11     a[0]=a[1]=a[2]=y;
12     while(a[0]<x)
13     {
14         ans++;
15         a[0]=min(a[1]+a[2]-1, x);
16         sort(a, a+3);
17     }
18     cout << ans << endl;
19     return 0;
20 }

 



苦难归于我，荣耀和鲜花也将归于我；     ------ geloutingyu

posted @ 2016-09-11 11:10  geloutingyu  阅读(165)  评论(0)  编辑  收藏  举报