Splay学习笔记

前面的话

HZ的人好像都学了Splay，讲题的人也经常说Splay，我校众神也都会Splay。

每次他们说Splay的时候我都说我不会太尴尬了，怒学Splay，学完之后真的感觉这是一种非常优美的数据结构。

概述

前置芝士：二叉搜索树

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；左、右子树也分别为二叉排序树
同样的序列，因为排序不同，可能会生成不同的二叉排序树，查找效率性对就不一定了。如果是二叉排序树退化成一条链，效率就很低。
（以上是抄的）

注意到最后一句，于是就出现了一堆平衡树，用来提高BST的效率，避免BST退化成链的问题。

GMK跟我说Treap没用，我就先学了Splay（

各种操作

Splay是一种优化过的BST，它通过伸展操作自我调整，提升效率。

首先得看一个旋转操作，它是伸展操作的实现基础。

旋转

你看这个树它吼不吼哇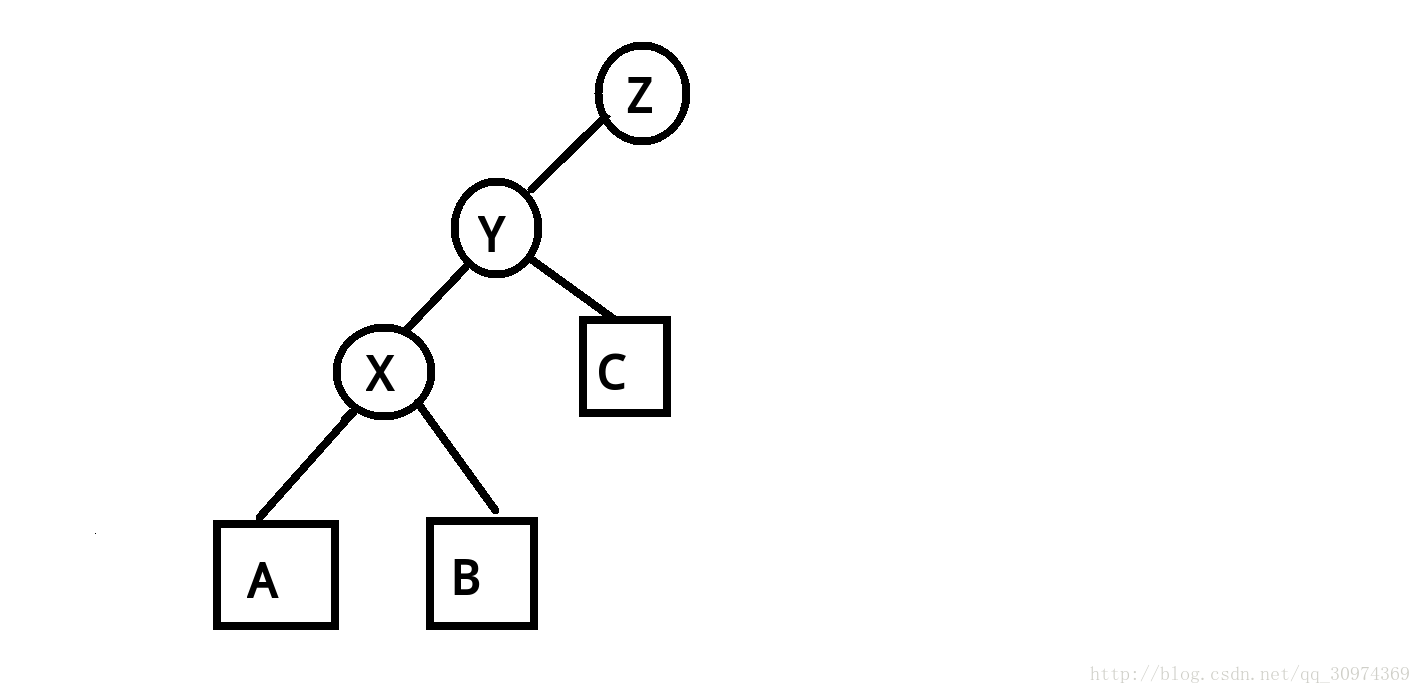

图是盗的

不吼哇！x那边太长啦，效率太低。于是我们把x转到y，重构树的结构，就能使树的深度更优。

如何旋转能不改变BST性质？

首先，y > x，所以y应该安置到x的右子树。然后把x连到z。y缺了个左儿子（它原来是有的），x多了个之前的右儿子，且这个右儿子必定小于y，所以把x的右儿子接成y的左儿子。

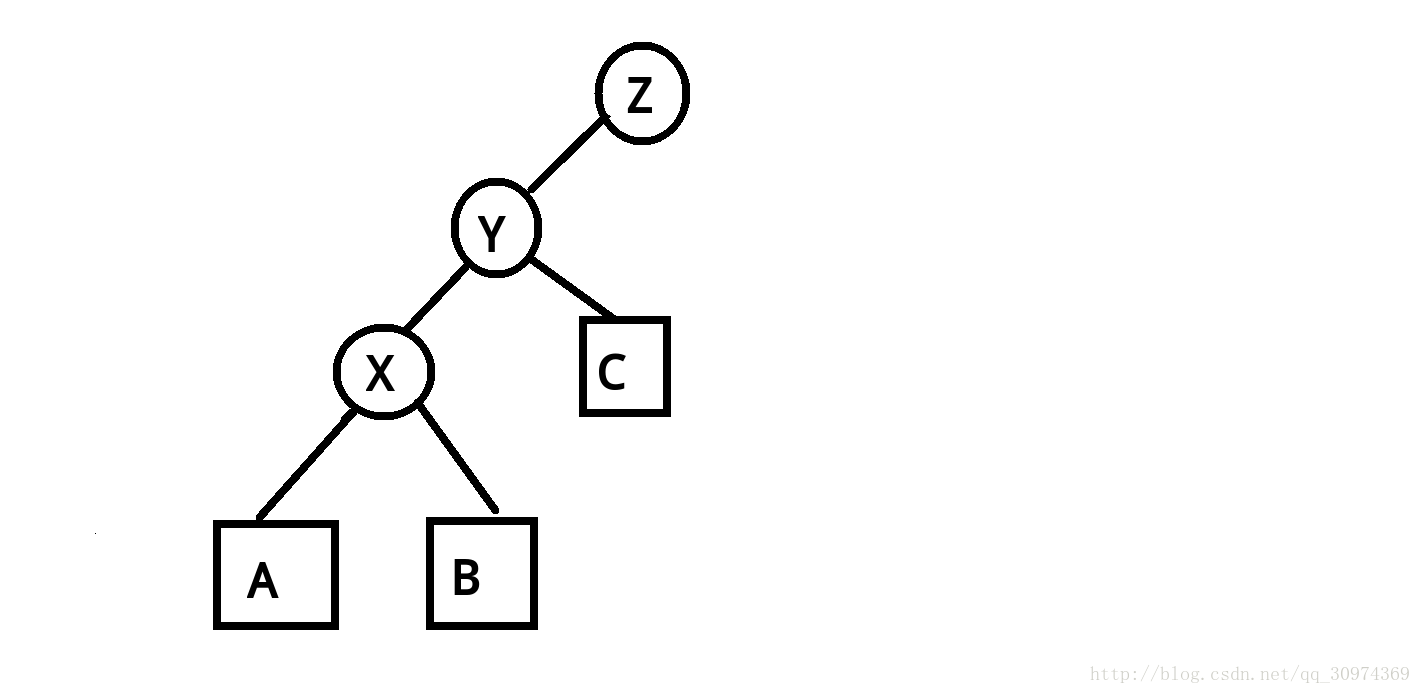
这是这个图的情况，总共有4种，没有人会闲的去写4个函数，要找普遍规律：x原来是y的哪个子树，x的这个子树就不会变，因为y会换掉另外一个子树。

To be continued...

模板：[LOJ #104. 普通平衡树] (https://loj.ac/problem/104)

#include <bits/stdc++.h>

const int N = 3e5 + 233, INF = 0x3f3f3f3f;
int n;

struct Splay {
    int root, tot, ch[N][2], siz[N], cnt[N], fa[N], val[N];
    Splay() {
        root = 1, ch[1][1] = 2;
        val[1] = -INF, val[2] = INF;
        cnt[1] = cnt[2] = 1;
        siz[1] = siz[2] = 1;
        fa[2] = 1, tot = 2;
    }
    inline int get(int x) { return ch[fa[x]][1] == x; }
    void update(int x) { siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + cnt[x]; }
    void rotate(int x) {
        int f1 = fa[x], f2 = fa[f1], id = get(x);
        ch[f1][id] = ch[x][id ^ 1], fa[ch[f1][id]] = f1;
        ch[f2][get(f1)] = x, fa[x] = f2;
        ch[x][id ^ 1] = f1, fa[f1] = x;
        update(f1);
    }
    void splay(int x, int goal = 0) {
        while (fa[x] != goal) {
            int f1 = fa[x], f2 = fa[f1];
            if (f2 != goal) {
                if (get(x) == get(f1))
                    rotate(f1);
                else
                    rotate(x);
            }
            rotate(x);
        }
        update(x);
        if (!goal)
            root = x;
    }
    void find(int x) {
        int p = root;
        while (ch[p][x > val[p]] && x != val[p]) p = ch[p][x > val[p]];
        splay(p);
    }
    void insert(int x) {
        int cur = root, p = 0;
        while (cur && val[cur] != x) p = cur, cur = ch[cur][x > val[cur]];
        if (cur)
            ++cnt[cur];
        else {
            cur = ++tot;
            if (p)
                ch[p][x > val[p]] = cur;
            ch[cur][0] = ch[cur][1] = 0;
            val[cur] = x, fa[cur] = p;
            cnt[cur] = siz[cur] = 1;
        }
        splay(cur);
    }
    int get_pre(int x) {
        find(x);
        if (val[root] < x)
            return root;
        int p = ch[root][0];
        while (ch[p][1]) p = ch[p][1];
        return p;
    }
    int get_nxt(int x) {
        find(x);
        if (val[root] > x)
            return root;
        int p = ch[root][1];
        while (ch[p][0]) p = ch[p][0];
        return p;
    }
    void remove(int x) {
        int pre = get_pre(x), nxt = get_nxt(x);
        splay(pre), splay(nxt, pre);
        int del = ch[nxt][0];
        if (cnt[del] > 1)
            --cnt[del], splay(del);
        else
            ch[nxt][0] = 0;
    }
    int get_kth(int k) {
        int p = root;
        while (1) {
            if (ch[p][0] && k <= siz[ch[p][0]])
                p = ch[p][0];
            else if (k > siz[ch[p][0]] + cnt[p])
                k -= siz[ch[p][0]] + cnt[p], p = ch[p][1];
            else
                return p;
        }
        return 0;
    }
} splay;

signed main() {
    scanf("%d", &n);
    for (int i = 1, opt, x; i <= n; i++) {
        scanf("%d%d", &opt, &x);
        switch (opt) {
            case 1:
                splay.insert(x);
                break;
            case 2:
                splay.remove(x);
                break;
            case 3:
                splay.find(x);
                printf("%d\n", splay.siz[splay.ch[splay.root][0]]);
                break;
            case 4:
                printf("%d\n", splay.val[splay.get_kth(x + 1)]);
                break;
            case 5:
                printf("%d\n", splay.val[splay.get_pre(x)]);
                break;
            case 6:
                printf("%d\n", splay.val[splay.get_nxt(x)]);
                break;
        }
    }
    return 0;
}