今天听一个教初中的朋友说,现在新教材中的概率问题都用“树形图”来求解了。在弄明白“树形图”是怎么回事后,我一开始认为没有必要引进“树形图”,因为其把简单问题搞复杂化了,可是后来仔细想一下,对于一个刚接触概率的初中生来说,“树形图”还是有其必要性的。
下面用一个例子来说明什么是“树形图”。
题:现有一黑一白两双袜子,从这4只袜子里任意取2只,颜色恰好一样的概率是多少?
解:将4只袜子分别编号为:黑1,黑2,白1,白2. 则树形图如下:

从图中可以看出,总共有12根连线,其中袜子颜色相同的有4根连线,所以概率 P = 4/12 = 1/3.
解毕。
我们再来看看用传统解法(即排列组合方法)如何做。由于上下标不好打,将从n个里面选m个的组合数表示成C(n,m)的形式。
解:从4只袜子里选2只,总共有 C(4,2) = 6 种可能:(黑1, 黑2), (黑1,白1), (黑1,白2), (黑2,白1), (黑2,白2), (白1,白2).
其中颜色相同的有2种,所以概率 P = 2/6 = 1/3.
解毕。
这样看来,传统方法更简洁,也不难理解,为什么还要引入树形图呢?我觉得是因为树形图表达形式直观,方法简单易掌握,更有利于引领初学者跨过概率那道门槛。我们之所以觉得传统方法简单,是因为我们已经做过很过概率题,对概率了解比较多了。对于一个刚接触概率的初中生来说,概率是一种全新的描述事情的方式,由于传统方法比较抽象,初学者想初步驾驭它需要比较长的时间,而不少人的信心会被这个过程中的挫折给慢慢磨掉。古人云,迟则生变,所以入门的过程越短越好。
下面,我将通过分析传统方法可能带来的错误答案来说明树形图对于初学者的优势所在,这些错误在长期的教学过程中会经常遇到,很有代表性。
- 错误解一:将选2只袜子看成每次选1只,选2次,则结果总共有4种可能:(黑,黑), (黑,白), (白,黑), (白,白). 所以概率 P = 2 /4 =1/2.
- 错误解二:2只袜子的颜色配对总共有3种可能:全黑、全白、一黑一白,所以概率 P = 2/3.
我们先来看下这些错误是发生在哪个环节的。
初中概率题目都为古典概率问题,做此类题时总共有三个步骤:
- 确定样本空间,即找出“所有可能出现的结果”
- 在样本空间中找出问题所对应的“基本事件”
- 相除算出概率
古典概率(classical probability),又称经典概率,它有如下特征: (1) 样本空间的元素(即基本事件)只有有限个。不妨设为n个,并记为w1, w2, …, wn. (2) 每个基本事件出现的可能性是相等的,即P(w1) = P(w2) = … = P(wn).
可以看出,第一步才是解题过程中最核心的和最难的,而且绝大部分错误都发生在这一环节(上面的两个错误也是),由于其他两步的错误很容易得到纠正,所以提高正确率的关键就在于提高第一步的正确率。
提高第一步正确率的方法说起来也很简单,就两条:
1. 提高学生的智力水平。比如让学生喝点“智力+10”的药水,或是改造大脑,提升大脑利用率之类的,当然,这些方法目前还是impossible mission,所以我们只能依靠第二个方法。
2. 降低第一步的难度。呃,这不是废话。我们仔细想一下,为什么传统方法会带来很多错误?我想一个原因就是传统方法没有一个直观的表现方式,是个比较抽象的方法,所以它依赖学生对于方法的理解程度。用传统方法教学时,老师会说这个题我们这样看,那个题那样看……,每个题都有实质相同却形式不同的看法,对于一个没有掌握其本质的初学者来说,你让他怎么认清众多看法中的相同之处,怎么从众多角度中选出正确的角度,怎么能不被搞蒙?如果能让可供选择的角度减少,甚至减至只有一种角度,难度是不是就大大降低了呢?那么,谁能办到?树形图说:“我能!”
为什么树形图可以办到?我认为有以下几个原因:
1. 树形图的实质是排列。它实际上就是排列方法的图形化表现方式,这点从前面的例子中就可以看出,所以用树形图解题时,不管题目是组合问题,还是排列问题,树形图把它们都当成排列问题来解了。这样讲解题方法就统一成了排列,相当于减少了可供选择的角度,从而降低了难度。
至于为什么可以用排列的方法来解组合问题,这里简单说一下。相信大家都知道,组合就是由排列去重后得来的,这点从公式中就可以看出:C(n,m) = A(n,m) / m!. 虽然用排列方法来解组合问题时,会使样本空间中有很多从现实意义上讲“重复”了的元素,但是没关系,这些“重复”都是成倍出现的,且倍数为m!,由于计算概率用的是除法,倍数m!最后会被约掉,所以我们能用排列的方法来解组合问题。
2. 由于树形图的实质是排列,所以它继承了用排列来解组合问题的优势,即避免了由排列转化为组合的过程中可能发生的错误。
为了说明这点,让我们回到之前列举的两个错误解法,仔细分析下这些错误是如何产生的。
首先,我们需要认为4只袜子是各不相同的。呃,我不是霸道地宣布它们就是不同的,因为袜子不仅只有颜色这个属性,还有长短、重量、褶皱程度……,各种属性,所以即使是同一双袜子,也总能找出其不同的地方。正如同世界上没有两片完全相同的树叶,也同样没有两只完全一样的袜子,:-) . 当然,我们做题时不用考虑这么多属性,我啰嗦这么多只是想说明即使是颜色相同的两只袜子也是不同的(这一点很重要). 那么,我们将这4只袜子重新编号为A, B, C, D, 且只考虑其颜色属性。为了方便表述,将它们用如下符号记录:(A: 黑), (B: 黑), (C: 白), (D: 白).
其次,由于我们研究的是由排列转化为组合的过程中错误是如何产生的,那么我们就要先用排列的视角来看“选了两只袜子”这个事情。众所周知,排列都是有顺序的。一般我们是用时间来区分不同的顺序,例如说,“第一次拿了一只黑色的袜子,第二次拿了白色的袜子。”如果非要有人和你较劲,说他能同时拿两只袜子,问你怎么区分(这种较劲行为是值得鼓励的,有助于发现问题的本质). 我想即使从时间上无法区分,那我还可以从空间上区分,因为你总不可能在现实中把两只袜子合到一起吧。那么,总会存在一个合适的方向,使得你在观察两只袜子时,会发现一只在前,另一只在后,这样顺序就有了,于是袜子又多了一个属性:顺序。我们将该属性的值定义如下,1:顺序一; 2:顺序二。
最后,我们就得到了由排列解法生成的样本空间Ω中的元素在新定义下的形式:
- {(A: 黑, 1), (B: 黑, 2)}, {(A: 黑, 1), (C: 白, 2)}, {(A: 黑, 1), (D: 白, 2)}
- {(B: 黑, 1), (A: 黑, 2)}, {(B: 黑, 1), (C: 白, 2)}, {(B: 黑, 1), (D: 白, 2)}
- {(C: 白, 1), (A: 黑, 2)}, {(C: 白, 1), (B: 黑, 2)}, {(C: 白, 1), (D: 白, 2)}
- {(D: 白, 1), (A: 黑, 2)}, {(D: 白, 1), (B: 黑, 2)}, {(D: 白, 1), (C: 白, 2)}
每一行对应之前图中的一棵树,每个元素都是由两只袜子组成,其中红色的是满足条件的元素。有了抽象的数学表示形式之后,我们就可以方便的讨论“转化过程”了。
我们知道,排列和组合唯一的区别在于:是否有顺序。也就是说,由排列转化为组合,只需要也只能丢弃“顺序”这个属性,如果丢弃错了属性,就会生成错误的样本空间。下面将展示正确方法和错误方法在转化过程中的区别。
正确方法:只丢弃“顺序”属性,通过排列生成的样本空间Ω转化为组合方法的样本空间,新空间元素如下(合并了相同的元素):
- {(A: 黑), (B: 黑)}, {(A: 黑), (C: 白)}, {(A: 黑), (D: 白)} , {(B: 黑), (C: 白)}, {(B: 黑), (D: 白)} , {(C: 白), (D: 白)}
错误一:形式上貌似是用了组合的方法,实际用的是排列,但是它丢弃了袜子的身份标识,认为只要颜色相同就是同一种袜子,所以得到了如下的样本空间:
- {(黑, 1), (黑, 2)}, {(黑, 1), (白, 2)}, {(白, 1), (黑, 2)}, {(白, 1), (白, 2)}
错误二:虽然是用组合的方法看问题,也丢弃了顺序属性,但同时也丢弃了袜子的身份标识,所以得到了如下的样本空间:
- {(黑), (黑)}, {(黑), (白)}, {(白), (白)}
经对比发现,两种错误都是由于丢弃了袜子的“身份标识”而产生的,而这个题目中隐含有不能丢弃“身份标识”的条件:那就是我们需要通过袜子的“身份标识”来区分最后选出的2只袜子,因为同一种颜色的袜子各有2只。
至此,我们已经弄明白了这些错误是怎么产生的,同时我们可以看到,如果直接用排列的方法解组合问题,就能避免这些错误的产生,这就是排列方法天生的优势所在。
3. 树形图是一种图形化表现形式,图形方法由于其直观性,相对于抽象的排列方法,它很容易被初学者掌握。
经过以上分析,我们已经能很清晰的看到为什么树形图有降低难度的能力了,所以新教材中采用这个方法也是合情合理,因为对初学者来说,首先也是最重要的是先跨过那道门槛。
前面谈了树形图这么多优点,现在来说说其缺点吧。由于树形图的实质是排列,所以它在继承排列优点的同时,也继承了排列的缺点:随着n的增长,A(n, m) 成阶乘倍增长!
当A(n, m)比较大的时候,用树形图解题就是个悲剧,下面我们看个“选边组成三角形”的例子。
题:从长度为1, 3, 5, 7, 9 的5条线段中任取三条,恰好能组成三角形的概率是多少?
解:由题意知,树形图中共有5棵树,根节点分别为1, 3, 5, 7, 9,画出树形图如下:
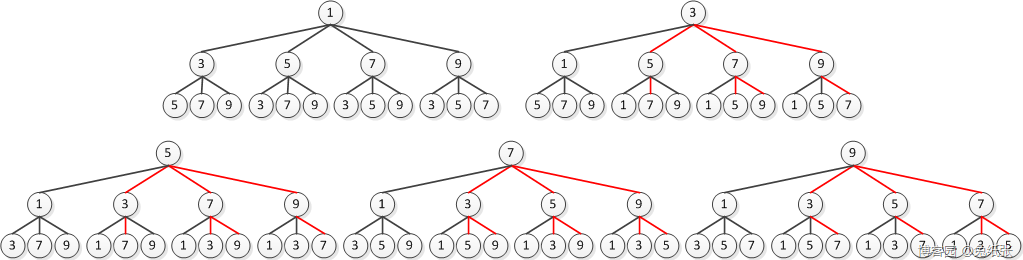
从图中可以看出,总共有5*12=60条路径,其中满足条件的路径有18条,所以概率 P = 18/60 = 3/10.
上图中共有85个节点,60条路径。先不说画出来有多麻烦了,就算画出来了,判断的时候只要漏掉一两条,答案就错了。
树形图用来处理情况较少的题目时还可以,碰到情况较多的题目就歇菜了。只会一种方法毕竟有其局限性,如果多数学生都学有余力,可以尝试教授传统方法。另外,我觉得如果教材改革了,相应的试题也应该改革,尽量少出情况很多的题目,否则就失去了改革的意义。
PS:在写本文时想到了一些其他内容,但和本文关联度不是很大,而且想法不是很成熟,如果日后有机会会再整理一片续出来。续篇中比较有意思的是:你会发现本文中出现的两种错误解法在某种意义下其实是正确的。
-------------------------------------------
作者:兔纸张 来源:博客园 ( http://www.cnblogs.com/geiliCode )





