聊聊人工智能的神奇公式：贝叶斯公式
贝叶斯公式由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展，用来描述两个条件概率之间的关系。贝叶斯原本是个神父，他为了证明上帝的存在而发明了著名的贝叶斯公式。然而他本人并不知道他所发明的公式及其背后的思想对当今社会产生重大变革，最典型的的莫过于当今炙手可热的“人工智能+”时代下，是人工智能的分支：机器学习，所必备的方法之一。
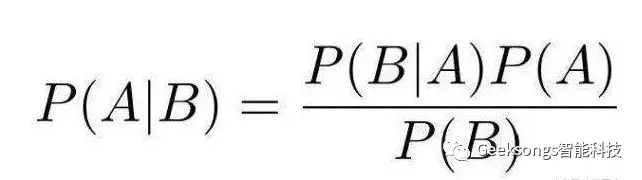
上图就是著名的贝叶斯公式，估计很多人和笔者一样看到数学公式就头疼，我们把翻译一下就很简单了。
-
P(A丨B)表达为：B这样的情况，A的可能性
-
P(B丨A)同理：A这样的情况，B的可能性
-
P(A)是A发生的可能性
-
P(B)是B发生的可能性，其中P(B)=P(B丨A)P(A)+P(B丨A')P(A')......这个叫做全概率公式（请参见浙大版《概率论与数理统计》P17）
-
用数学语言翻译就是：后验概率=先验概率*调整因子
下面我们用实例来看看贝叶斯公式是怎么使用的：
假设有两个班级其中1班有男生30人，女生20人；2班有男生25人、女生25人。体育老师抓到一个抽烟的男生，该男生打死也不告诉体育老师是那个班的。问题来了体育老师怎么判断该男生来自那个班？
很不巧我们的体育老师是个使用贝叶斯公式的高手（貌似体育老师的数学都是这么牛,毕竟笔者曾经所就读中学有个教得很好的数学老师以前就是体育老师）因此这点小问题可难不倒我们伟大的体育老师。
-
先将1班和2班标记为事件A1和事件A2，男生标记为事件B
-
那么我们所求的就是P(A1丨B)和P(A2丨B)
因为只有2个班那么我们先验概率P(A1)=P(A2)=50%；来自1班男生的概率P(B丨A1)=3/5：来自2班男生的概率P(B丨A2)=1/2
那么我们求出P(B)就可以代入公式得到结果:
P(B)=P(B丨A1)P(A1)+P(B丨A2)P(A2)=0.55
P(A1丨B)=P(B丨A1)P(A1)/P(B)=0.6*0.5/0.55=55%
P(A2丨B)=P(B丨A2)P(A2)/P(B)=0.5*0.5/0.55=45%
由结果我们可以得出：该男生来自1班的概率从50%（先验概率）上升到55%（后验概率）来自2班下降了5%
如果这时候生物老师走过来说了一句：2个班的男生没有几个留长头发。这时候有了新信息的加入，那么我们刚才计算的后验概率就变成了先验概率，继续代入公式来不断修正结果，这就是贝叶斯公式的强大之处。
这也是人类对人工智能的恐惧来源之一。
因为人工智能机器人没有感情，它只会根据人类输入的大数据通过贝叶斯公式不断修正结果而做出最有利的判断。当然我们的体育老师是个有感情的人类，它会把该男生抓去给2个班的班主任，不会像机器人一样那个概率高就选那个。不过我相信会有更好的公式出现，去模拟人类的情感。从而在艺术，情感上远超人类，而不是在逻辑上。这才是未来人工智能和平发展的趋势。
