单调神经网络《 Monotonic Networks》及代码实现
在金融风控领域当中,模型可解释性相当重要。我对nips的论文《Monotonic Networks》当中的单调神经网络进行了复现,在权重为正的情况下,我们就称该神经网络为单调神经网络,因为不管如何进行输入,我们输出都会呈现出单调性,也就是输入越大,输出越大。或者输入越大,输出越小。传统的单调神经网络设计十分简单,而最简单的则是仅有一层全连接神经网络,且神经元的权重全部为正/负,这样就能够保证神经网络的单调性。同时,在论文《 Monotonic Networks》当中,提出了一种更为创新的办法,在神经网络能够保证所有的权重为正/负的情况下,同时能够实现模型更高的准确性。我们来看看他是怎么实现的。
1.论文概述
在这里展示了这样一个模型,我们将其称为单调网络。单调网络通过对超平面组进行最大和最小操作来实现分段线性曲面。通过约束超平面权重的符号来强制执行单调性约束。可以使用通常与其他模型(例如前馈神经网络)一起使用的基于梯度的优化方法来训练单调网络。 Armstrong (Armstrong et. al. 1996) 开发了一种称为自适应逻辑网络的模型,它能够强制执行单调性,并且似乎与这里介绍的方法有一些相似之处。然而,自适应逻辑网络只能通过商业软件包获得。训练算法是专有的,尚未在学术期刊上完全披露。因此,单调网络代表(据我们所知)在学术环境中呈现的第一个模型,该模型具有强制单调性的能力。
我们来看看这个神经网络的架构如何:
该单调网络具有前馈、三层(两个隐藏层)架构。第一层单元计算输入向量的不同线性组合。如果特定输入需要增加单调性,则连接到该输入的所有权重都被约束为正。类似地,连接到需要降低单调性的输入的权重被限制为负数。第一层单元被分成若干组(每组的单元数量不一定相同)。对应于每个组的是第二层单元,它计算组内所有第一层单元的最大值。最终输出单元计算所有组的最小值。该神经网络的设计图如下:
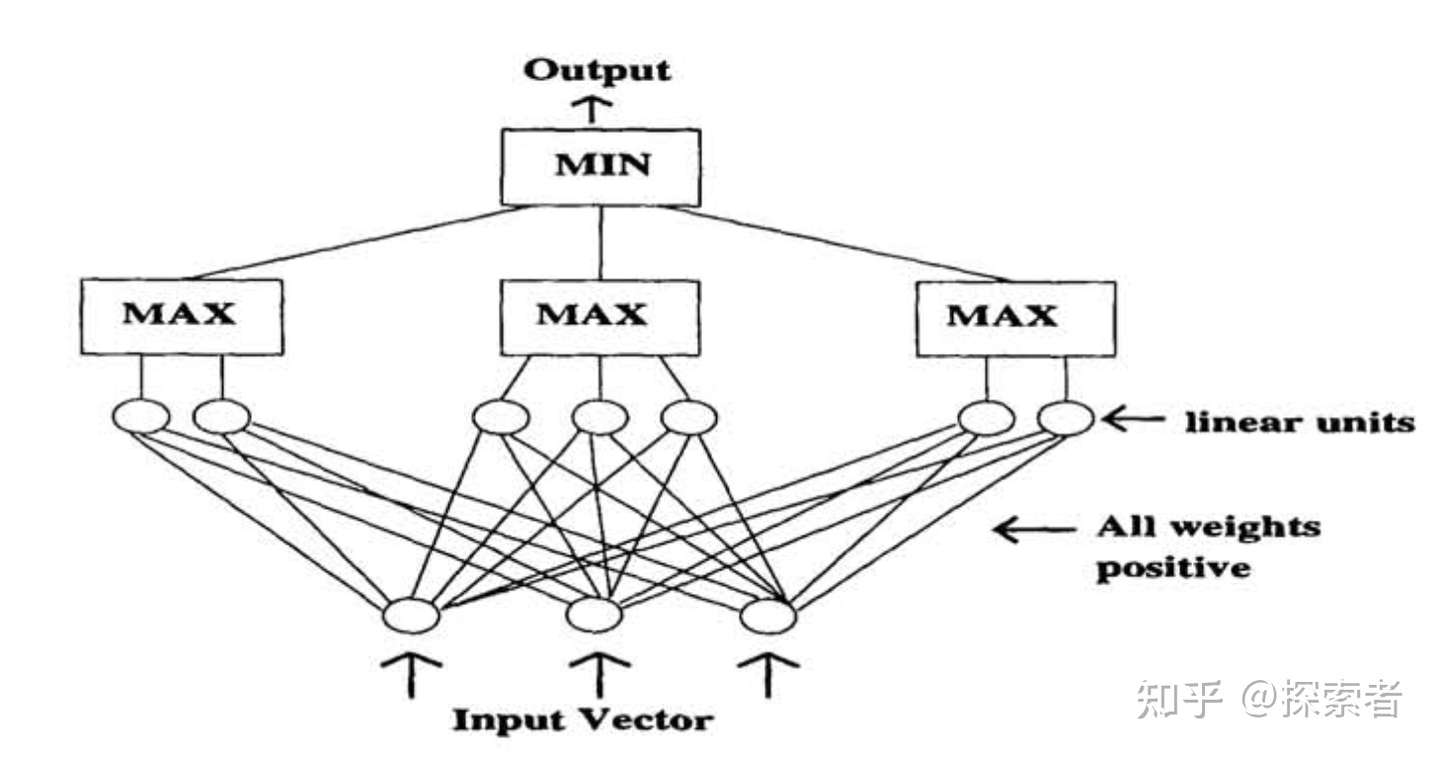 单调神经网络设计图
单调神经网络设计图
该神经网络第一层是我们的输入,第二层将我们输入放到一个全连接层当中,同时,分为3组(我们可以分为k组,看k的取值,怎样达到最好的模型识别准确率,你也可以尝试4,5,6......)。在这三组当中,我们分别找到每一组当中神经元输出最大的神经元,再将这些输出最大的3个神经元进行比较,将这3个神经元当中输出值最小的神经元作为我们的输出,最后通过sigmoid function,得到我们模型最好的输出。下面是该神经网络的数学表达式:
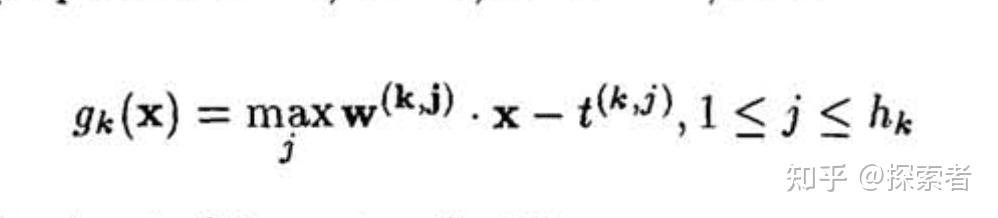 神经网络的第一层
神经网络的第一层
在以上公式当中, 表示第k组神经元的输出。如果我们分为了3组神经元,则k=3.
其中 表示第k组神经元当中第j个神经元的权重大小。
而后面的 则代表了偏执项。
假设我们令 为模型最后的输出,则有公式:
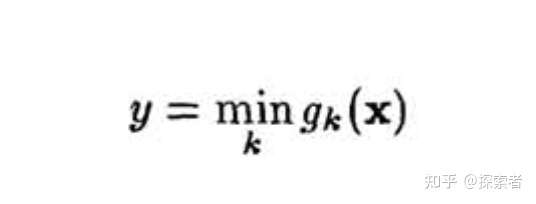
如果我们面对的是一个分类问题,则可以将最后的输入放进sigmoid function,公式如下:
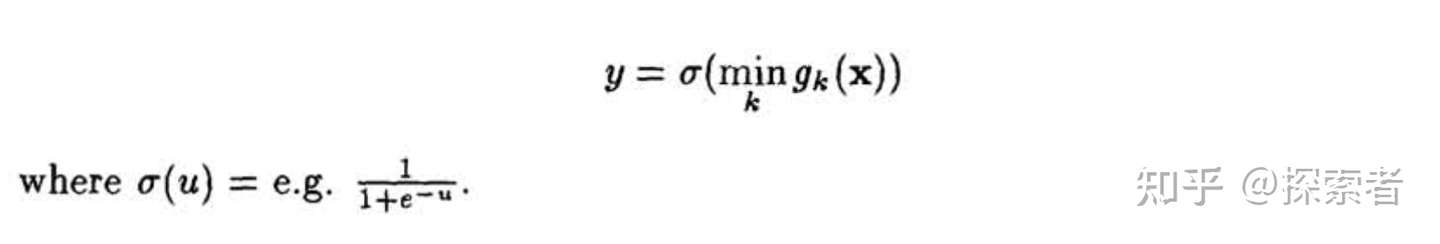
以上就是这个神经网络的整体实现。
2.代码实现
代码实现这一块我使用了pytorch来做的实现,神经网络架构可以编写如下:
import torch
from torch import nn
class MNET(nn.Module):
def __init__(self):
super().__init__()
self.layer_one = nn.Linear(32, 64) #将64个神经元,分为4组,每一组有16个神经元
self.sigmoid = nn.Sigmoid()
#forward这里就是神经网络的输入了
def forward(self, input_x):
length=len(input_x)
input_x = self.layer_one(input_x)
group_one=input_x[:,:,:16] #shape:[10,1,16],一共有16组神经元
group_two=input_x[:,:,:32]
group_three=input_x[:,:,:48]
group_four=input_x[:,:,:64]
#然后取每一个group当中,输出值最大的神经元
max_one=self.find_max(group_one)
max_two=self.find_max(group_two)
max_three=self.find_max(group_three)
max_four=self.find_max(group_four)
#然后找到这4组数据的最小值.每一个数据,只选取4个数据当中的一个
max_group=torch.cat((max_one,max_two),dim=1)#横着拼
max_group=torch.cat((max_group,max_three),dim=1)
max_group=torch.cat((max_group,max_four),dim=1)
return self.find_mini(max_group)
def find_max(self,group):
#这个找最大,的确应该在每一个数据当中找最大,如果每次在喂进的所有数据当中找最大,还是不靠谱的
max_ret=torch.max(group,dim=2)
return max_ret.values
def find_mini(self,group):
mini_ret=torch.min(group,dim=1)
return mini_ret.values.unsqueeze(-1)
由于在训练的过程当中,需要将所有的权重调整为正,因此需要如下代码调整权重的大小:
loss = criterion(out, var_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
for p in net.parameters():
p.data.clamp_(0, 99)
好啦,今天的分享就到这里啦!如果有收获的话,不要忘了点赞和收藏呀!




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 字符编码:从基础到乱码解决