【深度学习】:小白也能看懂的卷积神经网络
小编在市面看了很多介绍计算机视觉的知识,感觉都非常深奥,难以理解和入门。因此总结出了一套容易理解的教程,希望能够和大家分享。
一.人工神经网络
人工神经网络是一种模拟人脑构建出来的神经网络,每一个神经元都具有一定的权重和阈值。仅有单个神经元的图例如下所示:
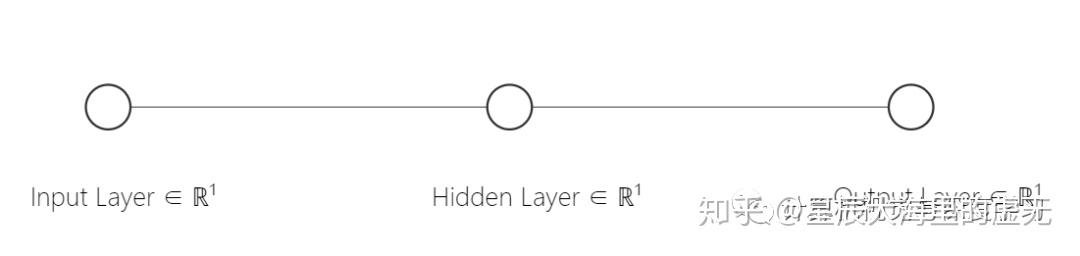
从中可以看到每一个神经元具有一个输入Input Layer,一个输出Ouput Layer。一般情况下,Input Layer仅有一个数值,Output Layer也仅是一个数值。中间的Hidden Layer则负责运算。而这个运算的过程我们使用了Sigmoid函数。这个函数是什么意思呢?假设我们输入的一个数值小于了某个阈值,那么神经网络的Output输出为0,大于这个阈值则输出1。而怎么在计算机当中用函数实现这个过程呢?科学家所构想的Sigmoid函数可以满足这一点,有了函数就可以将其放入到计算机当中进行运算啦!如下图所示。Hidden Layer当中的神经元就做如下的Sigmoid的运算,横坐标为输入Input Layer的值,纵坐标则代表Output Layer的值。
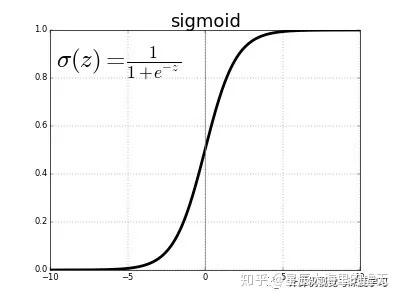
图1 Sigmoid function
我们可以从中看到,只要我们的输入值(横坐标)大于了5,输出值就十分逼近1,而小于了-5则十分逼近0,横坐标0是一个阈值(分界线)。这个函数的表达式在上图中也已经写出,也就是sigma(z)=1/(1+exp(-z))。这就是单个神经元之间是如何运算的方法,我们了解了单个神经元当中是如何运算的,就可以将其扩展到多个神经元了。


二.全连接神经网络
神经网络当中最基础的就是全连接神经网络了,在全连接神经网络每一层当中的一个神经元就与下一层的所有神经元都相连。神经网络可以分为输出层,输出层,和隐藏层,用于输入数据的层就是输入层,输出数据的是输出层,中间的所有层都叫做隐藏层。可以用下图来表示:

图 2 :全连接神经网络
在这个全连接神经网络当中,一共具有四个输入的值,因此第一个Input Layer具有四个点,中间则为Hidden Layer隐藏层,这里设置了五个神经元,最后Output输出层具有一个值。那么像这种类似的全连接神经网络可以做什么呢?就连这样一个简单的神经网络,稍作修改,用于做手写数字数字0-9的识别准确率就能够达到百分之97左右。对于识别手写数字而言,我们采用Mnist数据集,在这个数据集当中,每一幅数字的图片的分别率都是28*28,也就是一张图片上具有28*28个小方格,图像的长度为28个小方格,宽度也为28个小方格。每一个小方格上具有一个0-255之间的数字,这个数字代表了从黑色到白色的程度,0代表纯黑,255代表纯白。因此我们想要把数字输入到神经网络当中,也就是把这些小方格所对应的数字输入到神经网络当中,因此我们将输入层从刚才图中的4个,更改为28*28个,每一个节点用于接收一张手写数字图当中的一个小方格当中的数字,中间的隐藏层我们设定为30个神经元,输出设定为10个输出,因为有0-9一共十个数字,10个输出当中的其中一个输出都代表了识别为这个数字的概率。我们通过这个神经网络进行训练,通过使用Pytorch,Tensorflow等框架编写的代码,用Java实现可以使用DJL,或者在Java当中调用OpenCV即可。只要编写好这些神经网络每一层的架构,这个神经网络就会自动更新每一个神经元的权重,通过更新权重将最后输出的概率逼近于真实输入到神经网络当中的数字。
比如我们输入手写数字“1”,在输出层负责输出是否为数字“1”的神经元则会输出0.95,表示这个数字为1的概率为0.95,而其他输出层神经元的输出概率之和则为1-0.95=0.05。这就是全连接神经网络的作用了,目前还没有具体的理论能够解释究竟是为什么像这种神经网络的结构能够对数字进行识别达到如此高的准确度,但我们知道如果隐藏层所使用的神经元越多,隐藏层的层数越多,那么模型预测的精度就会越来越高,越大的神经网络也越容易训练。后来经过实验表明,在全连接层当中加入卷积神经网络层更能够增加神经网络识别的准确度,因为卷积神经网络的图像当中的特征提取能力会比全连接神经网络更强。

三.卷积神经网络
由于卷积神经网络对图像特征提取的能力会更强,在很多领域全连接神经网络并不是很管用,比如对一些更大的图片,图片当中并不是形状单一的数字,而是形形色色的动物,比如马,猫,狗等等。计算机要想对这些挑战性更大的图片进行识别,因此需要对图片特征进行一个更为有效的提取。根据实验证明,卷积神经网络能够很好地提取图片的特征,并对图像进行识别分类。为了更好的学习卷积神经网络,我们先介绍一些有关图像的知识。
在一般情况下图像是灰度图,也就是只有一个通道的黑白图像,一个图像只有一层。而对于彩色图像而言,一般具备三个通道,分别是红,黄,蓝三个通道,只要把这三个通道(可以理解为三层图像)叠加在一起,就可以在每一个像素点上显示出其他的颜色,因为所有的颜色都可以由红,黄,蓝这三个颜色组成。一张4*4的具有三个通道的彩色图像如下所示:
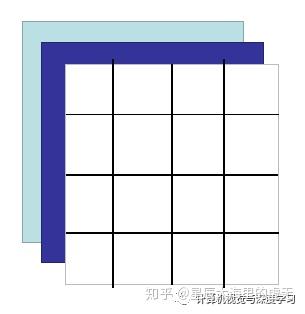
图3 :RGB图像
在这张图上的每一个小方格都具有一个0-255之间的数值,代表了颜色的深度。卷积神经网络如果想要对这张彩色的图像进行处理,其实也比较简单。卷积神经网络当中每一层都具有一个或者多个卷积核,我们先讨论仅有一个卷积核的情况。卷积核可以看作是一张仅有一个通道的图片,它的大小可以为为3*3,4*4,5*5等等。我们一般取3*3大小的作为我们的卷积核,也就是kernel size=3。那么卷积操作是如何进行的呢?卷积核如下图所示:
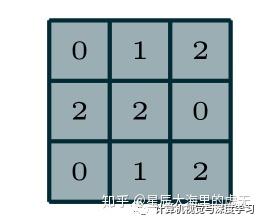
图4:卷积核
在卷积神经网络当中我们经常听到感受野这个学术词汇,感受野其实就是卷积核的大小,这两者之间并没有区别,只是换了一个说法而已。那么神经网络层之间的卷积是怎么进行操作的呢?假设我们的卷积核就采用上图当中的卷积核,对于需要进行卷积计算的图片为一张大小为5*5的灰度图片(并非RGB具有三通道的图片,这里仅仅只有一个通道)。我们让这个3*3的卷积核依次从左到右扫描过这张5*5的图像,扫描完一行之后再切换到下一行进行扫描,每扫描依次就做矩阵内积计算,使用这种方法计算出卷积之后的数值。在正常的卷积操作当中,卷积核的大小比图像的大小会更小,这样卷积核才能够在图像当中进行扫描,得到有效的信息。在最初还没有深度学习的时代,计算机科学家通过经验调整卷积核当中的数值,这样就可以进行各种各样的图像处理操作,只要稍微调整卷积核当中的数值,就可以在扫描完图像一次之后,将图像变模糊,或者在卷积完之后只保留图像当中物体的边缘。下面是卷积操作的具体过程:

图 5:卷积操作的实现
如上图所示,该图出自于论文《A guide to convolution arithmetic for deep learning》当中。这个卷积核在一个5*5的图像上不断扫描,输出了一个3*3的图像。这个图像上的数值是怎么通过矩阵内积计算出来的呢?很简单,在第一张图当中,我们的卷积核正好在覆盖在这幅图的左上方,覆盖到的图像里的数字依次为3,3,2,0,0,1,3,1,2。卷积核当中的数字则是0,1,2,2,2,0,0,1,2。内积操作则是将所有在空间上位置一致的数字对应相乘,再全部相加。卷积核当中的第一个数字和图像当中的第一个数字分别为3和0,因此相乘等于0。第二个小方格的乘积为3*1=3,然后计算出每一个小方格的乘积,最后将这些计算出来的乘积全部相加得到输出3*3图像当中的第一个数值。第一步计算的过程是:3*0+3*1+2*2+0*2+0*2+1*0+3*0+1*1+2*2=12。因此输出图像当中的第一个的数值为12,以此类推。在深度学习当中,卷积核当中的数字并非编程人员直接设定,而是通过这样的卷积神经网络训练出来的数值。
可能你会觉得疑惑,为什么卷积神经网络是一个网络呢,里面的操作并没有像全连接神经网络一样表示出来啊?也没有在刚才的操作当中看到一个网络啊?道理很简单,我们只需要把一个二维的图像展平,就变成了一个一维的网络,这样就可以作为输入直接将图像的信息“喂”到一个卷积神经网络里了。
卷积神经网络当中还有一个比较神奇的地方则是,假设我们输入的图像是一个3*3,具有三通道的RGB图像又该怎么办呢?是不是应该一张图想配备上三个卷积核呢?答案是:No!我们依然只需要一个卷积核就可以对这个三通道的RGB图像进行处理。只是在滑动卷积核的同时,要同时对三层图像做内积。也就是首先通过卷积计算出每一层的数值,再把这三层的所有数值都相加,就得到输出的数值。因此即使我们有三层图像的输入,最后得到也只是一个一维的图像。但我们也可以通过设计卷积核从而得到多个维度的图像,每一个卷积核都会扫描原图当中的所有部分从而得到一个输出维度(图像),我们想要输出多少个维度的图像,在卷积神经网络里设置多少个卷积核即可。
下面我们再来介绍一下卷积神经网络的参数。第一个也就是stride了,这个参数的中文含义是步伐,也就是卷积核在扫描图像时每扫描一次,是向右移动一步还是向右移动两步,三步等等。我们来看一个例子,在这个卷积操作当中,stride=2,用来做卷积操作的图像的大小依然为5*5,卷积核的大小为3*3,我们来看看这个怎么完成的:
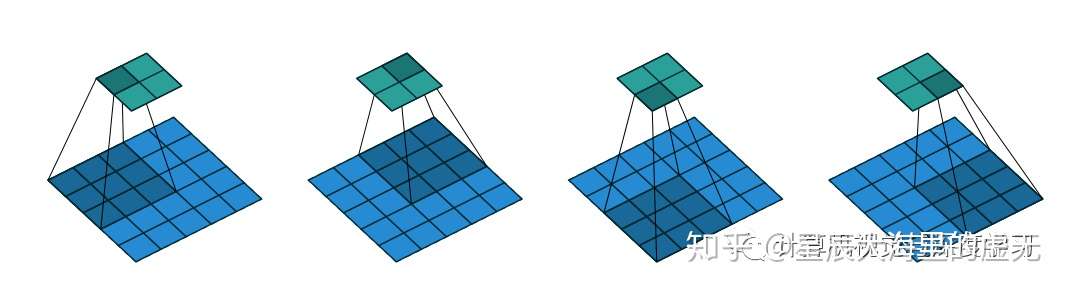
图 6:strde=2的卷积
在上面这张图中,输入的图像在最下方,而输出的图像在最上方。我们每移动一次卷积核就跳过了两个小方格,不管是从左向右移动还是从上往下运动,都跳过了两个小方格,因此我们的输出才是一个2*2的小方格。如果此时的stride设置为3,那么我们只会得到一个输出,因为卷积核不会因为stride太大就跳出原图像进行扫描。在stride为3的情况下我们只有增大原图像的大小才能够得到一个具有更多数字输出的图像。

四.图像的池化
在学习了神经网络和卷积神经网络的基础知识之后,我们就可以开始学习图像池化这一激动人心的知识了!在图像识别领域,世界上一些聪明的研究人员设计了不少效果相当不错的神经网络,比如 Alex Net, VGG, Google Net, ResNet等等。那么它们是怎么被设计出来的呢?
我们继续刚才的内容,深入了解一下卷积神经网络。在卷积神经网络当中,我们不仅仅有卷积的操作,还有一种叫做池化操作,这些图像识别的神经网络无非就是使用卷积操作和池化操作不断地重复,然后实验,调参,最后就可以设计出一个神经网络用于图像识别了!池化操作比卷积操作更加简单,一般情况下我们用到的有平均池化,还有最大池化。假设我们有一个4*4的图像,如下所示:
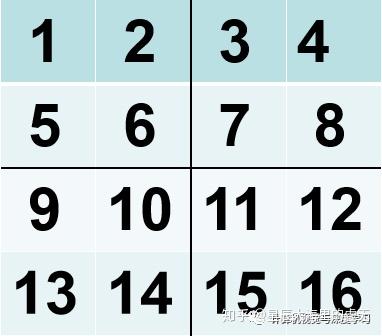
图7:池化图像
如果我们将其进行2*2的最大池化,也就是将这个4*4的图像分解成多个小的部分,每一部分都是一块2*2的小图像。在每一块2*2的图像当中取出一个最大的数值,这就是最大池化。在上图当中,第一小块图像的最大数值是6,第二块是8,第三块是14,第四块是16。因此做了最大池化之后输出的结果图如下所示:

图8:池化之后的输出
如果将图像做3*3的池化,也就是将图像全部分解成大小为3*3的小图像。然后根据是平均池化还是最大池化求出每一个输出小方格的值,平均池化就是把这个3*3的小图像求出平均值用于输出即可,之前我们这里没有提到。那么什么是用于图像识别的网络呢?
五.图像识别
图像识别技术是所有计算机视觉技术的基石,不管是目标检测,图像语义分割,目标跟踪,,ocr文字识别等等都需要图像识别技术作为基础。图像识别技术主要用于图像的分类,比如我们有一大堆已经标注好的猫猫和狗狗的图像,我们怎么让计算机也知道这些图像是猫猫还是狗狗呢?从计算机视觉的革命开始之时,Yun lecun在二十年前,也就是在1998年就提出的一种名叫LeNet的卷积神经网络用于数字分类,可以识别从0-9的数字。我们用这种卷积神经网络可以达到99.4%的识别准确率,在当时已经是像神一样的存在了,这个结果甚至比人类对验证码识别的准确率还要高。之前的全连接神经网络最多能够达到97%左右的准确率,但是越往上面走,连提升一个百分点都非常困难,那么这个神经网络的构造是什么样的呢?

图9:LeNet5 卷积神经网络架构
我们的输入层,是一系列32*32的手写字体图片,这些手写字体包含0~9数字,相当于10个类别的图片输出的结果是分类的结果,也就是0~9之间的所数所预测得到的概率值。在我们训练时,只能够把图像一张一张地送进神经网络,每一张图像都是32*32,因此这个神经网络的输入神经元有32*32=1024个。接着第二层就进入了我们的卷积神经网络层,在论文当中采用了6个卷积核,每一个卷积核的大小为5*5.然后进行最大池化,将输出的Ouput的大小减半,之后又对池化的结果做卷积操作,卷积核依然选择5*5,但是这时使用了16个卷积核,因此会输出16个通道的图片,我们可以将通过卷积操作之后的图像称之为特征图(Feature Map)。然后再做最大池化,将特征提取得更加抽象,池化之后又卷积。最后经过双层全连接神经网络,第一层全连接层具有128个神经元,第二层有84个神经元,这些具体神经元的个数都是调参和实验的结果,最后得到10个输出,代表了每个数字所输出的概率。这样,LeNet-5就设计完成了。当然,后续的研究者参照LeNet-5的研究思想又发明了其他的神经网络,后来发明的神经网络则可以用来做任意物体的图像分类,这些新发明为如今如火朝天的计算机视觉技术奠定了巨大的基础。
今天小编的分享就到这里啦!
终于写完啦,如果觉得读了小编的文章您有收获的话,不要忘记了点击下方的“推荐”哦!您的支持就是对小编创作最大的动力!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号