《剑指offer》2:青蛙跳台阶
一.题目:
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
二.题目分析
拿到这个题目我们冥思苦想也没有想到一个好的想法,于是从最简单的找规律开始吧!
另台阶的级数为n,跳法的数量为ret.
n=1, ret=1
n=2, ret=2
n=3, ret=3
n=4, ret=5
n=5, ret=8
如下图所示: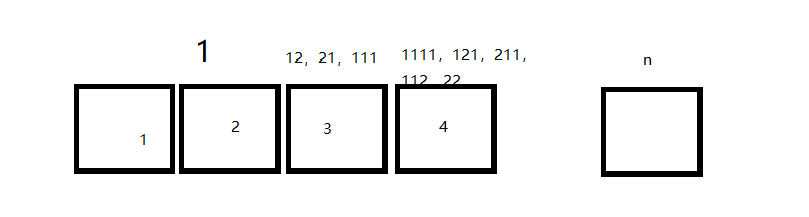
从中分析可得ret等于上一个ret的值加上 上上个ret的大小。就如同斐波那契数列一样,但是这只是一个猜想,具体是不是这样的呢?
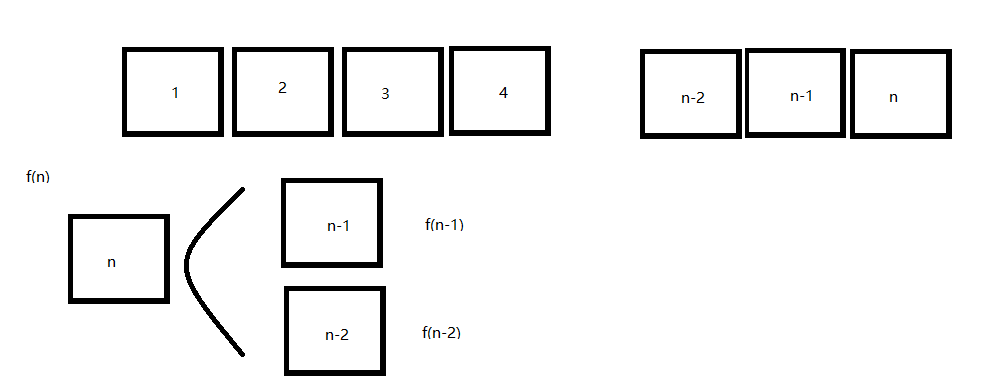
我们换一个思考的方向,让青蛙从第n个台阶往回跳,记在第n个台阶时可能跳的跳法为f(n)个。假设它往回跳只跳了一格,那么停留在n-1处,还有f(n-1)种跳法,假设他往回跳了2格,那么它还具有f(n-2)中跳法,一共就具有这两种情况,因此f(n)=f(n-1)+f(n-2),这个表达式正好和斐波那契数列的递归解法的表达式相同,因此也可以使用同样的迭代解法来求解这个问题,同时这也证明了我们之前的猜想是正确的。如下图所示:
三.代码实现
代码实现就很简单了,实现和斐波那契数列差不多,如下所示:
# -*- coding:utf-8 -*- class Solution: def jumpFloor(self, number): # write code here if number<1: return 0#在Number小于1的时候 if number==1: return 1 if number==2: return 2 ret=0 a=1 b=2 for i in range(3,number+1): ret=a+b a=b b=ret return ret
得解,牛客网上显示:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号