开发高效算法之初窥
算法时间复杂度的常用递推关系
递归关系对于分析算法时间复杂度非常有用,下表总结了常用的地推关系:
| 递推关系 | 复杂度结果 | 示例 |
|---|---|---|
| T(n)=T(n/2) + O(1) | T(n) = O(logn) | 二分查找 |
| T(n)=T(n-1) + O(1) | T(n) = O(n) | 线性查找 |
| T(n)=2T(n/2) + O(1) | T(n) = O(n) | 寻最值的二分递归查找 |
| T(n)=2T(n/2) + O(n) | T(n) = O(nlogn) | 归并排序 |
| T(n)=T(n-1) + O(n) | T(n) = O(n^2) | 选择排序 |
| T(n)=2T(n-1) + O(1) | T(n) = O(2^n) | 汉诺塔 |
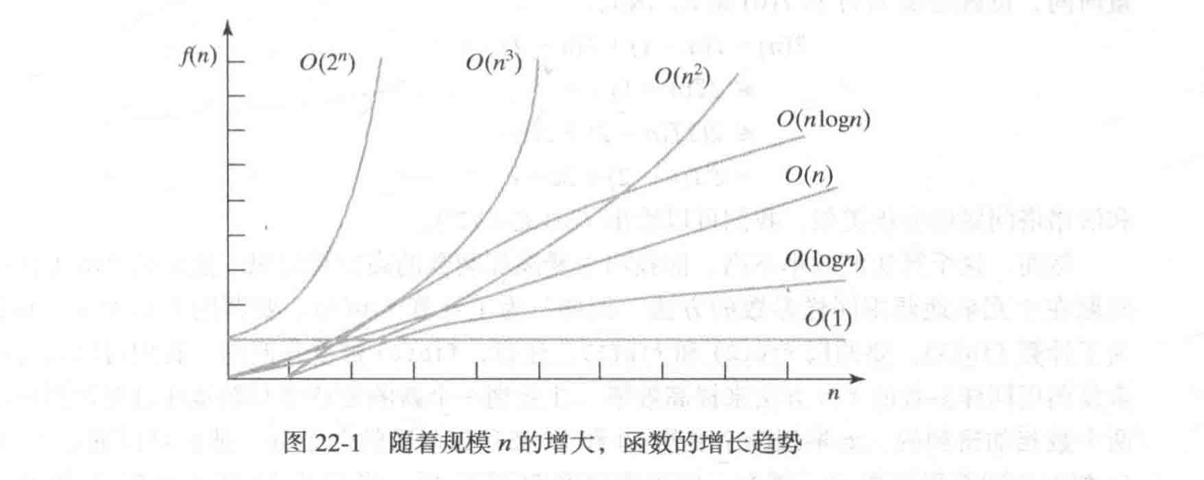
不同复杂度函数的比较关系如下:
O(1) < O(log n) < O(n) < O(nlogn) < O(n^2) < O(2^n)
算法示例
字符串的最长非递减子串
public static String maxConsecutiveSortedSubstring(String s) {
int maxSize = 1;
int tmpbeg = 0;
int beg = 0;
int tmpMax = 1;
for (int i=1; i < s.length(); i++) {
if (s.charAt(i) >= s.charAt(i-1)) {
tmpMax++;
if (tmpMax > maxSize) {
maxSize = tmpMax;
beg = tmpbeg;
}
} else {
tmpMax = 1;
tmpbeg = i;
}
}
return s.substring(beg, beg + maxSize);
}
动态规划求斐波那契序列
public class Fibnacci {
public static long fib(long n) {
long f0 = 0;
long f1 = 1;
long f2 = 1;
if (n==0)
return f0;
else if (n==1)
return f1;
else if (n==2)
return f2;
for (int i=3; i <=n; i++) {
f0 = f1;
f1 = f2;
f2 = f0 + f1;
}
return f2;
}
}
动态规划通过解决子问题,然后将子问题的结果结合来获得整个问题的解的过程。这自然地引向递归的解答。然而,使用递归效率不高,因为子问题相互重叠了。动态规划的关键思想只解决子问题一次,并将子问题的结果以备后用,从而避免了重复的子问题求解。
求最大公约数的欧几里得算法
public class EuclidGCD {
public static int gcd(int m, int n) {
if (m % n == 0)
return n;
else
return gcd(n, m%n);
}
}
埃拉托色尼筛选法求素数
import java.util.Scanner;
public class SieveOfEratosthenes {
public static void main(String[] args) {
System.out.println("Find all prime numbers <= n.");
int n = input.nextInt();
boolean[] primes = new boolean[n+1];
for (int i=0; i < primes.length; i++) {
primes[i] = true;
}
for (int k = 2; k <= n/k; k++) {
if (primes[k]) {
for (int i = k; i<=n/k; i++) {
primes[k*i] = false; // k*i is not prime
}
}
}
int count = 0;
for (int i=2; i<primes.length; i++) {
if (primes[i])
count++;
}
System.out.println("\n" + count + " prime(s) less than or equal to " + n);
}
}
分治方法与最近点对问题
分而治之(divide-and-conquer),这个方法将问题分解为子问题,解决子问题,然后将子问题的解答合并从而获得整个问题的解答。和动态规划方法不同的是,分而治之方法中的子问题不会交叉。子问题类似初始问题,但具有更小的规模,因此可以应用递归来解决这样的问题。事实上,所有的递归的解答都遵循分而治之方法。
步骤1: 以x坐标的升序对点进行排序,对于x坐标一样的点,按它的y坐标排序,这样就得到一个排好序的点构成的线性表S;
步骤2: 使用排好序的线性表的中点将S划分为两个大小相等的子集S1和S2,让中点位于S1。递归地找到S1和S2中的最近点对,设d1和d2分别表示两个子集中最近点对点距离。
步骤3: 找出S1和S2中点点之间距离最近点点对,它们之间的距离用d3表示,则最近的点对距离为min(d1, d2, d3)的点对。
import java.util.Arrays;
import java.util.ArrayList;
public class ClosedPair {
public static Pair getClosestPair(double[][] points) {
Point[] pointsOrderedOnX = new Point[points.length];
for (int i = 0; i < pointsOrderedOnX.length; i++)
pointsOrderedOnX[i] = new Point(points[i][0], points[i][1]);
return getClosestPair(pointsOrderedOnX);
}
public static Pair getClosetPair(Point[] points) {
Arrays.sort(points);
// Locate the identical points if exists
Pair pair = checkIdentical(points);
if (pair != null)
return pair; // The distance between the identical points is 0
Point[] pointsOrderedOnY = points.clone();
Arrays.sort(pointsOrderedOnY, new CompareY());
return distance(points, 0, points.length - 1, pointsOrderedOnY);
}
/** Locate the identical points if exist */
public static Pair checkIdentical(Point[] pointsOrderedOnX) {
Pair pair = new Pair();
for (int i = 0; i < pointsOrderedOnX.length - 1; i++) {
if (pointsOrderedOnX[i].compareTo(pointsOrderedOnX[i + 1]) == 0) {
pair.p1 = pointsOrderedOnX[i];
pair.p2 = pointsOrderedOnX[i + 1];
return pair;
}
}
return null;
}
public static Pair distance(Point[] pointOrderedOnX, int low, int high, Point[] pointsOrderedOnY) {
if (low >= high) // Zero or one point in the set
return null;
else if (low + 1 == high) {
// Two points in the set
Pair pair = new Pair();
pair.p1 = pointsOrderedOnX[low];
pair.p2 = pointsOrderedOnX[high];
return pair;
}
// Step 2
int mid = (low + high) / 2;
Pair pair1 = distance(pointsOrderedOnX, low, mid, pointsOrderedOnY);
Pair pair2 = distance(pointsOrderedOnX, mid + 1, high, pointsOrderedOnY);
double d;
Pair pair = null;
if (pair1 == null && pair2 == null) {
d = Double.MAX_VALUE;
} else if (pair1 == null) {
d = pair2.getDistance();
pair = pair2;
} else if (pair2 == null) {
d = pair1.getDistance();
pair = pair1;
} else {
d = Math.min(pair1.getDistance(), pair2.getDistance());
if (pair1.getDistance() <= pair2.getDistance())
pair = pair1;
else
pair = pair2;
}
// Obtain stripL and stripR
ArrayList<Point> stripL = new ArrayList<Point>();
ArrayList<Point> stripR = new ArrayList<Point>();
for (int i = 0; i < pointsOrderedOnY.length; i++) {
if (pointsOrderedOnY[i].x <= pointsOrderedOnX[mid].x
&& pointsOrderedOnY[i].x >= pointsOrderedOnX[mid].x - d)
stripL.add(pointsOrderedOnY[i]);
else if (pointsOrderedOnY[i].x > pointsOrderedOnX[mid].x
&& pointsOrderedOnY[i].x <= pointsOrderedOnX[mid].x + d)
stripR.add(pointsOrderedOnY[i]);
}
// Step 3: Find the closest pair for a point in stripL and
// a point in stripR
double d3 = d;
int r = 0;
for (int i = 0; i < stripL.size(); i++) {
while (r < stripR.size() && stripL.get(i).y > stripR.get(r).y + d)
r++;
// Compare a point in stripL with at most six points in stripR
int r1 = r; // Start from r1 up in stripR
while (r1 < stripR.size() && stripR.get(r1).y <= stripL.get(i).y + d) {
if (d3 > distance(stripL.get(i), stripR.get(r1))) {
d3 = distance(stripL.get(i), stripR.get(r1));
pair.p1 = stripL.get(i);
pair.p2 = stripR.get(r1);
}
r1++;
}
}
return pair;
}
public static double distance(Point p1, Point p2) {
return distance(p1.x, p1.y, p2.x, p2.y);
}
public static double distance(double x1, double y1, double x2, double y2) {
return Math.sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
}
/** Define a class for a point with x- and y- coordinates */
static class Point implements Comparable<Point> {
double x;
double y;
Point(double x, double y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Point p2) {
if (this.x < p2.x)
return -1;
else if (this.x == p2.x) {
// Secondary order on y-coordinates
if (this.y < p2.y)
return -1;
else if (this.y == p2.y)
return 0;
else
return 1;
} else
return 1;
}
}
/**
* A comparator for comparing points on their y-coordinates. If y-coordinates
* are the same, compare their x-coordinator.
*/
static class CompareY implements java.util.Comparator<Point> {
public int compare(Point p1, Point p2) {
if (p1.y < p2.y)
return -1;
else if (p1.y == p2.y) {
// Secondary order on x-coordinates
if (p1.x < p2.x)
return -1;
else if (p1.x == p2.x)
return 0;
else
return 1;
} else
return 1;
}
}
/** A class to represent two points */
public static class Pair {
Point p1;
Point p2;
public double getDistance() {
/* if (p1 == null || p2 == null)
return Double.MAX_VALUE;
else */
return distance(p1, p2);
}
@Override
public String toString() {
return "(" + p1.x + ", " + p1.y + ") and (" + p2.x + ", " + p2.y + ")";
}
}
}
回溯法与八皇后问题
回溯法(backtyacking)渐进地寻找一个备选方案,一旦确定该被选方案不可能是一个有效方案的时候则放弃掉,继而寻找一个新的备选方案。
public class EightQueens {
private static final int SIZE = 8;
private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};
// check if a queen can be placed at row i and column j
private boolean isValid(int row, int column) {
if (queens[row-i] == column // check column
|| queens[row-i] == column - i // check upleft diagonal
|| queens[row-i] == column + i) //check upright diagonal
return false; // there is a conflict
return true;
}
private int findPosition(int k) {
int start = queens[k] + 1; // search for a new placement
for (int j = start; j < SIZE; j++) {
if (isValid(k, j))
return j; // (k, j) is the place to put the queen now.
}
return -1;
}
public boolean search() {
int k = 0;
while (k >= 0 && k < SIZE) {
int j = findPosition(k);
if (j < 0) {
queens[k] = -1;
k--;
} else {
queens[k] = j;
k++;
}
}
return (k==-1)? false:true;
}
}
附:递归解法
public class EightQueens {
private static final int SIZE = 8;
private int[] queens = new int[SIZE]; // queen positions.
// check if a queen can be placed at row i and column j
private boolean isValid(int row, int column) {
for (int i==1; i <= row; i++)
if (queens[row-i] == column // check column
|| queens[row-i] == column - i // check upleft diagonal
|| queens[row-i] == column + i) // check upright diagonal
return false; // there is a conflict
return true;
}
private boolean search(int row) {
if (row == SIZE) // stop condition
return true; // a solution found to place 8 queens in 8 rows.
for (int column=0; column<SIZE; column++) {
queens[row] = column; // place q queen at (row, column)
if (isValid(row, column) && search(row+1))
return true; // found, thus return to exit for loop
}
// no solution for a queen placed at any column of this row
return false;
}
public boolean search() {
return search(0);
}
}




