向量、矩阵和张量的导数
向量、矩阵和张量的导数
[著] Erik Learned-Miller
本文翻译自 Vector, Matrix, and Tensor Derivatives
本人英语水平有限,文章中有翻译不到位的地方请热心指出并改正!
本文的目的是帮助学习向量(vectors)、矩阵(matrices)和更高阶张量(tensors)的导数,关于向量、矩阵和高阶张量求导。
1 简化,简化,简化
关于对数组求导的许多困惑都来自于想要一次性做太多的事情。这些“事情”包括一次性同时对多个组成部分的公式进行求导,在求和符号前面求导和应用链式求导法则。通过做这些事情的同时,我们更有可能犯错,至少在我们有经验之前是这样的。
1.1 扩展符号到显式求和方程式的每个部分
为了简化一个给定的计算,对于输出的单个标量元素(a single scalar element)除了标量变量(scalar variables)写出显示公式通常是非常有用的。一旦对于输出的单个标量元素根据其它标量值有一个显式的公式,然后就可以使用微积分计算,这比同时尝试做所有的矩阵数学、求和和求导工作要简单得多。
Example. 假如我们有一个由一个 \(C\) 行 \(D\) 列的矩阵 \(W\) 乘以一个长度为 \(D\) 的列向量 \(\vec{x}\) 得到的长度为 \(C\) 的列向量 \(\vec{y}\) :
假如我们对 \(\vec{y}\) 关于 \(\vec{x}\) 的导数感兴趣。这个导数的完整表征需要 \(\vec{y}\) 的每一个分量关于 \(\vec{x}\) 的每一个分量的(偏)导数,在这个例子中,将包含 \(C\times D\) 个值,因为 \(\vec{y}\) 中有 \(C\) 个分量,在 \(x\) 中有 \(D\) 个分量。
让我们开始计算其中的一个,对于 \(\vec{y}\) 的第 \(3\) 个分量关于关于 \(\vec{x}\) 的第 \(7\) 个分量;即我们想要计算:
这只是一个标量关于另一个标量的导数。
要做的第一件事就是写出对于计算 \(\vec{y}_3\) 的公式,然后我们就可以对其求导。从矩阵-向量相乘的定义,\(\vec{y}_3\) 的值通过 \(W\) 的第 \(3\) 行和向量 \(\vec{x}\) 的点积计算得到:
此时,我们将原先的矩阵方程(公式 \((1)\) )简化为一个标量方程。这使得计算想要的导数更加容易。
1.2 移除求和符号
因为直接计算公式 \((2)\) 的导数是可以的,人们经常犯的错误就是当微分表达式中包含求和符号(\(\sum\))或是连乘符号(\(\prod\))。当我们开始计算时,写出来不包含任何求和符号确保做的每一步都是正确的有时候是非常有用的。使用 \(1\) 作为第一个索引,我们有:
当然,我们明确地包括了含有 \(\vec{x}_7\) 这一项,因为这就是我们在此的不同之处。此时,我们可以看到对于 \(y_3\) 仅依赖在 \(\vec{x}_7\) 之上的表达式只有 \(W_{3,7}\vec{x}_7\) 这一个项。因为在累加中没有其它项包括 \(\vec{x}_7\) 即它们关于 \(\vec{x}_7\) 的导数都是 \(0\) 。因此,我们有:
通过关注在 \(\vec{y}\) 的一个分量和 \(\vec{x}\) 的一个分量,我们尽可能地简化计算。在未来,当你感到困惑时,尝试减少一个问题最基本的设置可以帮助你查看哪里出错。
1.2.1 完善导数:雅可比(Jacobian)矩阵
回想我们的原始目标是计算 \(\vec{y}\) 每一个分量关于 \(\vec{x}\) 的每一个分量的导数,并且我们注意到其中会有 \(C\times D\) 个。它们可以写成如下形式的一个矩阵:
在这个特别的例子中,这个矩阵被称为雅可比矩阵(Jacobian matrix),但是这个术语对于我们的目的不重要。
注意对于如下方程:
\(\vec{y}_3\) 关于 \(\vec{x}_7\) 的部分简单地由 \(W_{3,7}\) 给出。如果你做相同的处理方式到其它部分上,你将会发现,对于所有的 \(i\) 和 \(j\) :
这意味着偏导数的矩阵是
当然,这就是 \(W\) 本身。
因此,做完这些所有工作后,我们可以得出结论
我们有
2 行向量而不是列向量
在使用不同的神经网络包时要密切关注权重(weight)矩阵和数据矩阵等的排列方式是很重要的。举个例子,如果一个数据矩阵 \(X\) 包含许多不同的向量,每一个向量表示一个输入,矩阵 \(X\) 的一行或是一列哪一个是数据向量?
在第一章节的例子中,我们使用的向量 \(\vec{x}\) 是一个列向量。但是,当 \(\vec{x}\) 是一个行向量时你也应该有能力使用同样的基础想法。
2.1 Example 2
令 \(\vec{y}\) 的长度为 \(C\) 的行向量(row vector)是由另一个长度为 \(D\) 的行向量 \(\vec{x}\) 与 \(D\) 行 \(C\) 列的矩阵 \(W\) 相乘得到。
重要地是,尽管 \(\vec{y}\) 和 \(\vec{x}\) 依旧有着相同数量的成分,\(W\) 的形状(shape)是我们之前使用的 \(W\) 的形状的转置(transpose)。尤其是,因为我们现在使用 \(\vec{x}\) 左乘,然而,之前的 \(\vec{x}\) 是在右边的,\(W\) 对于矩阵代数必须是转置的才行得通。
在这个例子,你将会看到,通过写出
得到
注意到 \(W\) 的索引是与第一个例子是相反的。但是,当我们组成所有的雅可比矩阵,我们仍然可以看到此例中也是
3 高于两维的处理
让我们来考虑另一个密切相关的问题,计算
在这个例子中,\(\vec{y}\) 变量沿着一个坐标变化而 \(W\) 变量沿着两个坐标变化。因此,全部的导数最自然地包含在三维数组中。我们避免术语“三维矩阵(three-dimensional matrix)”,因为如何做定义在三维数组上的矩阵相乘和其它矩阵运算是不清晰的。
三维数组的处理,找到一种输出排列它们的方法可能会变得更加麻烦。相反,我们应该简单地定义我们的结果为可以适用于所需三维数组的任意一个元素结果的公式。
让我们再次计算在 \(\vec{y}\) 上的一个分量的标量导数,比如 \(\vec{y}_3\) 和 \(W\) 的一个成分,比如是 \(W_{7,8}\) 。让我们从相同的基本设置开始,其中我们根据其它标量分量写下一个 \(\vec{y}_3\) 的等式。现在,我们想要一个根据其它标量值表示 \(\vec{y}_3\) 的等式,并且显示出 \(W_{7,8}\) 在它的计算中扮演的角色。
但是,我们可以看到,\(W_{7,8}\) 在 \(\vec{y}_3\) 的计算中是没有作用(no role)的,因为:
换句话说,即:
但是,\(\vec{y}_3\) 关于 \(W\) 的第 \(3\) 列元素的偏导数将一定不为 \(0\) 。举个例子,\(\vec{y}_3\) 关于 \(W_{2,3}\) 的导数如下给出:
其可以通过公式 \((8)\) 简单地看出。
总的来说,当 \(\vec{y}\) 的分量的索引等于 \(W\) 的第二个索引,导数就将非零,同时对于其它情况就为零。我们可以写出:
但是其它三维数组的元素将会是 \(0\) 。如果我们令 \(F\) 表示 \(\vec{y}\) 关于 \(W\) 的导数的三维数组,其中:
则
对于 \(F\) 的其它元素都为零。
最后,如果我们定义一个新的二维(two-dimensional)数组 \(G\) 为:
我们可以看到我们需要关于 \(F\) 的所有信息都被存放到 \(G\) 中,并且 \(F\) 有用的(non-trivial)部分实际上是二维的,而不是三维的。
在高效的神经网络实现中,将导数数组中重要的部分以一个紧凑的方式表示出是至关重要的。
4 多个数据点
重复之前的一些例子是很好的练习,并且使用 \(\vec{x}\) 的多个例子,堆叠在一起形成一个矩阵 \(X\) 。让我们假设每一个单独的 \(\vec{x}\) 是一个长度为 \(D\) 的行向量,\(X\) 是一个 \(N\) 行 \(D\) 列的二维数组。作为我们的上一个例子,\(W\) 将会是一个 \(D\) 行 \(C\) 列的矩阵。\(Y\) 由下给出:
也是一个 \(N\) 行 \(C\) 列的矩阵。因此,\(Y\) 的每一行将给出与输入 \(X\) 的相应行的相关联的行向量。
坚持我们写出一个对于给定的输出成分的表达式的技术,我们有:
我们立即可以从这个等式中看到导数:
除了 \(a=c\) 的情况,它们都为零。这也就是因为每一个 \(Y\) 的分量仅仅通过 \(X\) 的相应的行计算得到,\(Y\) 和 \(X\) 的不同行之间分量的导数都为零。
此外,我们可以看到:
这完全不取决于上面我们正在比较的 \(X\) 和 \(Y\) 的行。
实际上,矩阵 \(W\) 保持所有的这些部分,我们只需要记住根据公式 \((10)\) 索引到其中来获得我们想要的具体的偏导数。
如果我们令 \(Y_{i,:}\) 为 \(Y\) 的第 \(i\) 行,令 \(X_{i,:}\) 为 \(X\) 的第 \(i\) 行,我们就可以看到:
这是一个我们之前由公式 \((7)\) 得到的结果的简单的归纳。
链式法则与向量和矩阵的结合
现在我们已经解决了几个基础的例子,让我们结合这些思想到一个链式法则(chain rule)的例子上。同样,假设 \(\vec{y}\) 和 \(\vec{x}\) 都是列向量,让我们从这个等式开始:
并且尝试计算 \(\vec{y}\) 关于 \(\vec{x}\) 的导数。我们应该简单地观察两个矩阵 \(V\) 和 \(W\) 的乘积不过是另一个矩阵,记作 \(U\) ,因此
但是,我们想要通过使用链式法则的处理得到中间结果的定义,以便我们可以看到在这种情况下链式法则如何应用到非标量导数上。
让我们定义中间结果:
然后我们有:
然后我们使用链式法则写出:
为了确保我们准确地知道这是什么意思,让我们一次分析一个分量的老方法,以 \(\vec{y}\) 的一个分量和 \(\vec{x}\) 的一个分量开始:
但是我们应该如何准确地解释右边的乘积?链式法则的思想是以 \(\vec{y}_i\) 关于每一个标量(each scalar)中间变量的变化乘以(multiply)每一个标量中间变量关于 \(\vec{x}_j\) 的变化。尤其如果 \(\vec{m}\) 由 \(M\) 个分量组成,然后我们写出:
回想我们之前关于一个向量关于一个向量的导数的结果:
就是 \(V_{i,k}\) 并且:
就是 \(W_{k,j}\) 。所以我们可以写出:
其就是对 \(VW\) 的分量表达式,就是我们原先对这个问题的答案。
总结一下,我们可以在向量和矩阵导数的背景下使用链式法则:
- 明确说明中间结果和用于表示它们的变量
- 表示最终导数各个分量的链式法则
- 对链式法则表达式内的中间结果上适当求和

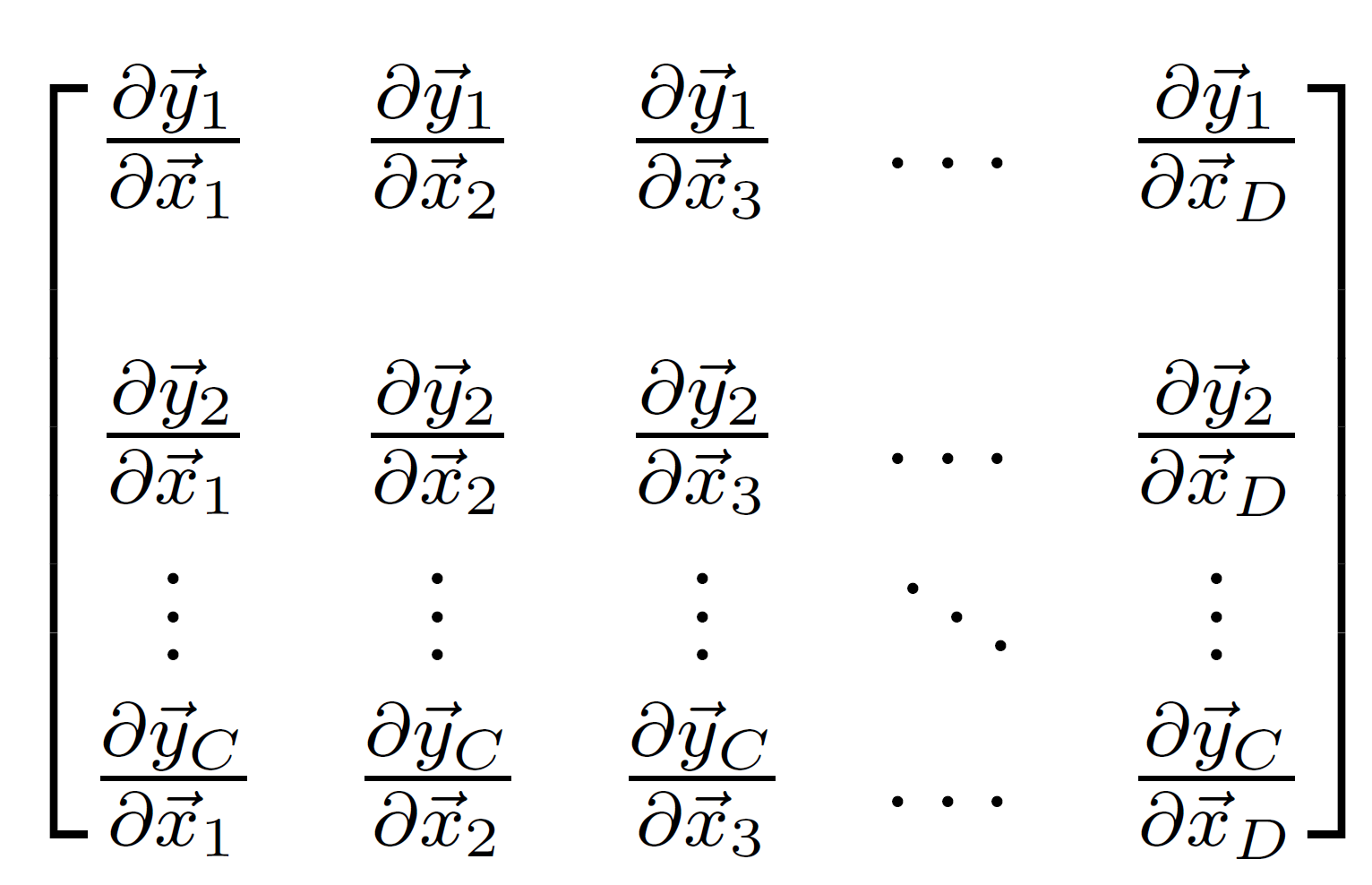 本文讲述了关于向量、矩阵和张量之间的求导的一些知识和方法,其中包含了两个向量之间的求导,向量与矩阵的导数,如何处理更高维数的数组(张量),最后如何在矩阵和向量的导数上运用链式法则。
本文讲述了关于向量、矩阵和张量之间的求导的一些知识和方法,其中包含了两个向量之间的求导,向量与矩阵的导数,如何处理更高维数的数组(张量),最后如何在矩阵和向量的导数上运用链式法则。
