Python之禅——逐句解读
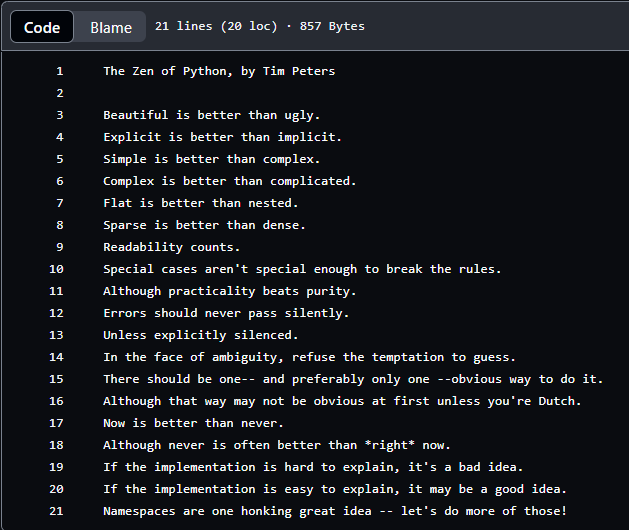
以下便是著名的PEP20 ----《The Zen of Python》全文
站在前人的肩膀上,从哲学的角度逐句细品下python
理解用到了大模型: Claude3
PEP 20 – The Zen of Python
1. Beautiful is better than ugly.
# 优雅的风格 names = ['Alice', 'Bob', 'Charlie'] print(', '.join(name for name in names)) # 丑陋的风格 names = ['Alice', 'Bob', 'Charlie'] print_str = '' for name in names: print_str += name + ', ' print(print_str[:-2])
优雅的代码不仅结构清晰,而且更加简洁易读。在这个例子中,第一种方式使用列表推导式和str.join()方法,代码更加简洁优雅。
2. Explicit is better than implicit.
# 显式优于隐式 from math import sqrt # 显式调用sqrt函数 result = sqrt(4) print(result) # 输出: 2.0 # 隐式计算平方根 result = 4 ** 0.5 print(result) # 输出: 2.0
显式编码有利于代码的可读性和可维护性。在这个例子中,第一种方式直接调用sqrt函数,意图更加明确。
3. Simple is better than complex.
# 简单的实现 def is_even(num): return num % 2 == 0 # 复杂的实现 def is_even(num): sqrt = num ** 0.5 int_part = int(sqrt) decimal_part = sqrt - int_part if decimal_part == 0: if int_part % 2 == 0: return True else: return False else: return num % 2 == 0
简单的代码更容易理解和维护。在这个例子中,第一种实现只需要检查余数是否为0,而第二种实现过于复杂。
4. Complex is better than complicated.
稍有费解,这句翻译:"复杂胜于混乱。"
在这里,“复杂”指的是系统或解决方案的结构,而“混乱”指的是实现或使用时的不必要困难或混乱。换句话说,它意味着设计时可以有一些复杂性,但实现和使用时不应该让人感到困惑或混乱。
# 复杂但不复杂的实现 def fibonacci(n): if n <= 1: return n else: return fibonacci(n - 1) + fibonacci(n - 2) # 复杂且复杂的实现 def fibonacci(n): a, b = 0, 1 for _ in range(n): a, b = b, a + b return a
复杂但不复杂的代码可以更好地表达其意图。在这个例子中,第一种递归实现虽然复杂,但更易于理解斐波那契数列的定义。第二种实现虽然简单,但代码的意图不太明确。
5. Flat is better than nested.
# 扁平的结构 matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ] result = [] for row in matrix: for item in row: result.append(item) print(result) # 输出: [1, 2, 3, 4, 5, 6, 7, 8, 9] # 嵌套的结构 matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ] result = [] for i in range(len(matrix)): for j in range(len(matrix[i])): result.append(matrix[i][j]) print(result) # 输出: [1, 2, 3, 4, 5, 6, 7, 8, 9]
扁平的结构通常更容易理解和维护。在这个例子中,第一种实现使用了嵌套的列表推导式,代码更加简洁和直观。
6. Sparse is better than dense.
# 稀疏的数据结构 sparse_vector = {0: 1, 3: 5, 8: 2} # 1的索引是0, 5的索引是3, 2的索引是8 # 密集的数据结构 dense_vector = [1, 0, 0, 5, 0, 0, 0, 0, 2]
在某些情况下,稀疏的数据结构可以更高效地利用内存和计算资源。在这个例子中,稀疏向量只储存非零元素及其索引,而密集向量需要存储所有元素。
7. Readability counts.
# 可读性差的代码 def f(x): return x**2 + 5*x + 3 # 可读性好的代码 def calculate_quadratic(x, a=1, b=5, c=3): """ 计算二次函数 ax^2 + bx + c 的值. 参数: x (int或float): 自变量的值 a (int或float): 二次项系数,默认为1 b (int或float): 一次项系数,默认为5 c (int或float): 常数项,默认为3 返回: int或float: 二次函数的值 """ return a * x**2 + b * x + c
可读性是编码过程中非常重要的一个方面。在这个例子中,第二个函数使用了描述性的变量名和函数名,并添加了文档字符串,提高了代码的可读性。
8. Special cases aren't special enough to break the rules.
# 违反规则的特殊情况 class SpecialString(str): def __len__(self): return 0 # 总是返回0,违反了len()的语义 # 遵守规则的实现 class SpecialString(str): def __new__(cls, value, special_length): instance = str.__new__(cls, value) instance.special_length = special_length return instance def __len__(self): return self.special_length
在第一个例子中,我们定义了一个SpecialString类,继承自str。在这个类中,我们重写了__len__方法,使其总是返回0,而不是字符串的实际长度。这种做法破坏了len()函数的语义,违反了Python中"一致性"的规则。
在第二个例子中,我们也定义了一个SpecialString类,但是以一种更合理的方式实现了特殊的长度功能。我们在__new__方法中接受一个special_length参数,并将其存储在实例属性中。然后,我们重写了__len__方法,使其返回这个特殊长度,而不是破坏len()的语义。
这个例子更好地体现了"Special cases aren't special enough to break the rules"的含义。即使我们需要处理一些特殊情况,也不应该违反Python的基本规则和语义。相反,我们应该在不破坏规则的前提下,设计合理的解决方案来满足特殊需求。
通过这个例子,我们可以看到,第一种实现方式违反了规则,而第二种实现方式则遵循了规则,同时也满足了特殊需求。这就是这条理念所强调的核心思想。
9. Although practicality beats purity.
# 纯粹但不实用的实现 def fibonacci(n): if n <= 1: return n else: return fibonacci(n - 1) + fibonacci(n - 2) # 实用但不纯粹的实现 fibonacci_cache = {} def fibonacci(n): if n in fibonacci_cache: return fibonacci_cache[n] if n <= 1: result = n else: result = fibonacci(n - 1) + fibonacci(n - 2) fibonacci_cache[n] = result return result
这个例子体现了"Although practicality beats purity"这条理念。第一种实现是一个纯粹的递归函数,用来计算斐波纳契数列。它的实现精确地符合斐波纳契数列的数学定义,因此具有一定的"纯粹性"。然而,这种实现在计算较大的数字时,由于重复计算的缘故,效率会变得非常低下。
为了提高效率,第二种实现引入了一个缓存机制。它利用了一个字典fibonacci_cache来存储已经计算过的斐波纳契数值,在需要重复计算时直接从缓存中取值。这种实现虽然牺牲了一些"纯粹性"(不再严格遵循斐波纳契数列的数学定义),但是它更加实用,计算效率大大提高。
这个例子说明,在实际编程中,我们有时需要在"纯粹性"和"实用性"之间做出权衡。虽然"纯粹性"具有一定的优点(如更好地符合数学定义、更加简洁等),但"实用性"往往更加重要,因为它直接关系到代码的性能和可用性。在一些情况下,我们不得不放弃一些"纯粹性",以换取更好的"实用性"。
总的来说,这条理念提醒我们,在设计和编码时,应该以"实用性"为首要考虑因素,而不是过于追求"纯粹性"。一个实用但不那么"纯粹"的解决方案,通常比一个"纯粹"但不实用的解决方案更加可取。
10. Errors should never pass silently. Unless explicitly silenced.
# 隐式地让错误通过 try: result = 1 / 0 except ZeroDivisionError: pass # 显式地处理错误 try: result = 1 / 0 except ZeroDivisionError as e: print(f"Error: {e}")
这条理念强调,错误不应该被默认忽略,除非有明确的理由。在第一个例子中,ZeroDivisionError被隐式地忽略了,这可能会导致潜在的bug。
而在第二个例子中,错误被显式地捕获并打印出来,程序的行为更加明确。
11. In the face of ambiguity, refuse the temptation to guess.
# 猜测导致模棱两可 def parse_integer(value): try: return int(value) except ValueError: # 猜测value可能是一个浮点数 return int(float(value)) # 拒绝猜测 def parse_integer(value): try: return int(value) except ValueError as e: raise ValueError(f"Invalid integer value: {value}") from e
当代码存在模棱两可的情况时,不应该尝试去猜测,而应该明确地拒绝这种情况。
在第一个例子中,parse_integer函数试图猜测输入值是否为浮点数,这可能会导致意外的行为。
而在第二个例子中,函数直接抛出一个明确的ValueError,拒绝了猜测的诱惑。
12. There should be one-- and preferably only one --obvious way to do it.
# 多种实现方式 result = [x * x for x in range(10)] # 或 result = [] for x in range(10): result.append(x * x) # 一种明显的实现方式 result = [x ** 2 for x in range(10)]
这条理念鼓励代码只有一种明显的实现方式,避免出现多种等价的解决方案。
在第一个例子中,计算平方的操作有两种不同的实现方式,这可能会导致混乱。
而在第二个例子中,使用列表推导式计算平方是一种更加明显的实现方式。
13.Although that way may not be obvious at first unless you're Dutch.
这条理念是一个幽默的评论,暗示即使有一种明显的实现方式,对于一些人来说也可能不那么明显,除非你是荷兰人。
它提醒我们,即使遵循了上一条理念,代码的可读性和易理解性仍然需要考虑不同的背景和文化。
# 一种"明显"的实现方式 def sum_of_squares(numbers): total = 0 for x in numbers: total += x ** 2 return total # 对一些人而言不太"明显"的实现 def sum_of_squares(numbers): return sum(x ** 2 for x in numbers)
对于大多数人来说,第一种实现方式可能是比较"明显"的。它使用了一个for循环来遍历列表中的每个元素,对每个元素求平方,然后累加到total变量中。这种实现方式符合大多数人的直觉,因此可以认为是"明显"的。
但是,对于一些人来说,特别是那些精通函数式编程或者Python高级特性的人,第二种实现方式可能更加"明显"。它利用了Python的生成器表达式(x ** 2 for x in numbers)和sum()内置函数,以一种更加简洁和"Python化"的方式实现相同的功能。
这个例子说明,即使是一种被认为"明显"的实现方式,对于某些特定群体来说也可能不太"明显"。这就是这条理念所暗示的内容:代码的可读性和易理解性并不是一成不变的,它取决于读者的背景和文化。
一个荷兰程序员可能会觉得第二种实现方式更加"明显",因为荷兰有着函数式编程和Python的传统。而一个其他国家的初学者可能会觉得第一种实现方式更加"明显"。
因此,这条理念提醒我们,在编写代码时,不能仅仅依赖于自己的直觉和判断。我们应该考虑代码的可读性和易理解性对不同读者群体的影响,尽量使代码对大多数人都足够"明显"。同时,也要意识到总会有一些人觉得某些实现方式"不明显",这是难以完全避免的。
14. Now is better than never.
# 现在就做 def factorial(n): result = 1 for i in range(1, n + 1): result *= i return result # 永不实现 # ... 无代码示例 ...
这条理念鼓励我们现在就去做,而不是拖延。在上面的例子中,factorial函数提供了计算阶乘的实现,而不是永远拖延下去。及时地解决问题通常比一直拖延要好。
15. Although never is often better than right now.
# 立即实现可能导致低质量代码 def fizz_buzz(n): # 草率的实现... return [] # 等待一段时间后再实现 def fizz_buzz(n): result = [] for i in range(1, n + 1): item = "" if i % 3 == 0: item += "Fizz" if i % 5 == 0: item += "Buzz" if not item: item = str(i) result.append(item) return result
这条理念是对上一条的补充,提醒我们虽然要及时行动,但有时候等待一段时间再实现也是更好的选择,以获得更高质量的代码。
在第一个例子中,fizz_buzz函数的实现是草率的,可能会导致低质量的代码。
而在第二个例子中,经过一些思考后,函数的实现更加完整和正确。
16. If the implementation is hard to explain, it's a bad idea.
# 难以解释的实现 def obscure_code(n): result = (lambda x: x * (x + 1) // 2)(n) # ... 更多难以解释的代码 ... return result # 易于解释的实现 def calculate_triangular_number(n): """ 计算第n个三角形数. 三角形数是一个等差数列,公式为: n * (n + 1) / 2 """ return n * (n + 1) // 2
这条理念强调,如果一段代码的实现很难解释,那它很可能是一个不好的想法。在第一个例子中,obscure_code函数的实现使用了lambda表达式和其他难以理解的代码,这使得它很难被解释。
而在第二个例子中,calculate_triangular_number函数的实现更加直观,并且有详细的文档字符串解释了它的作用和计算方式。
17. If the implementation is easy to explain, it may be a good idea.
# 易于解释的实现 def is_palindrome(s): """ 判断一个字符串是否为回文串. 回文串是一个正反读都一样的字符串. """ return s == s[::-1]
如果一段代码的实现易于解释,那它很可能是一个好的想法。在这个例子中,is_palindrome函数的实现非常简单,只需要将原字符串与其反转后的字符串进行比较。
该实现易于解释,因此可以认为它是一个好的想法。
18. Namespaces are one honking great idea -- let's do more of those!
# 使用命名空间 import math def calculate_area(radius): return math.pi * radius ** 2 def calculate_circumference(radius): return 2 * math.pi * radius
这条理念赞扬了命名空间的概念,鼓励我们更多地使用命名空间。在这个例子中,math模块提供了一个命名空间,包含了许多与数学相关的函数和常量,如pi。
通过使用命名空间,我们可以组织和管理代码,避免命名冲突,并提高代码的可读性和可维护性。
以上就是我根据Python之禅的每一条理念提供的代码示例和解释。我尽力使用简单而直观的例子,帮助你更好地理解这些理念在实际代码中的应用。如果有任何疑问或需要。
【翻译与理解】:
- 命名空间可真是个绝赞的好主意 -- 我们要多多使用它们!
解释如下:
- "one honking great idea" 这个俚语用词,用来形容某件事情非常出色、了不起。"honking"一词源自honk(honking是它的现在分词形式),本意是"汽车喇叭声"、"鸣笛声"。但在这种俚语用法中,它强调了"great"的程度,表示非常了不起。
- "let's do more of those!"这句话的语气是积极鼓励的,表达了要大量采用和使用命名空间这个好主意。
所以,这个翻译力求保留原句的活泼口语化语气,并适当地转换成地道的中文表达。它更好地传达了Python之禅在赞扬命名空间这一理念时的热情和鼓舞语气。
相比之下,直译为"命名空间是一个很棒的主意 -- 让我们多使用它们!"虽然意思没错,但语气就显得生硬和缺乏活力了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号