2017清北学堂(提高组精英班)集训笔记——备战指导与往年经典例题
一、比赛策略:
1.比赛成绩=比赛经验×自身实力。
2.比赛前在不断提高自己实力的同时,积累大量经验。
3.千万不要copy代码,不过可以抄代码,看到优秀的代码,边抄边想这个是怎么来的,抄多了自然就会熟练,最好抄到你打键盘都手软!
4.平时比赛多写写对拍,比赛时候就写得出了,能大幅提高正确率。
5.正式比赛的时候最主要的就是细心,拿能拿到的分数。
6.要有自信->我不拿第一谁拿第一??
二、乱入两个钟神的Tips:
①我们在读入long long类型数据时,要根据评测程序的操作系统来选择是"%I64d"还是"%lld",但是很麻烦啊,有没有什么办法不用这样搞?
肯定有啊!只要在程序头文件下方加上这些代码即可!
1 #include <stdio.h> 2 #ifdef WIN32//以下自动判断当前系统! 3 #define LL "%I64d" 4 #else 5 #define LL "%lld" 6 #endif 7 int main() 8 { 9 int x=100; 10 long long gg=200; 11 printf("%d " LL,x,gg); 12 return 0; 13 } 14 /* 15 output: 16 100 200 17 */
②C++中还有long double这个类型的数,但不能读入和输出,只能在计算过程中使用!
三、往年经典例题:
经典例题:借教室(Luogu 1083 NOIP2012 D2T2)
其中第i天学校有ri个教室可供租借。
共有m份订单,每份订单用三个正整数描述,分别为dj,sj,tj,表示某租借者需要从第sj天到第tj天租借教室(包括第sj天和第tj天),每天需要租借dj个教室。
即对于每份订单,我们只需要每天提供dj个教室,而它们具体是哪些教室,每天是否是相同的教室则不用考虑。
借教室的原则是先到先得,也就是说我们要按照订单的先后顺序依次为每份订单分配教室。如果在分配的过程中遇到一份订单无法完全满足,则需要停止教室的分配,通知当前申请人修改订单。这里的无法满足指从第sj天到第tj天中有至少一天剩余的教室数量不足dj个。
求至少到第几个订单无法满足条件。
数据范围:1≤n,m≤106,0≤ri,dj≤109,1≤sj≤tj≤n。
算法描述:
这个题实际上就是让我们维护区间减法和求区间最小值操作。
做法一:线段树(70分)
两个操作:①将[dj,sj]的值同时减少tj;②查询最小值是否<0。
做法二:二分订单数(100分)
假如前x个订单能满足要求,那么前x-1个订单也一定能满足要求;
假如前x个订单不能满足要求,那么前x+1个订单也一定不能满足要求。
二分答案mid→判断前mid个订单能否满足要求,如果可以,答案≥mid,否则答案<mid。
操作:s[dj]=s[dj]+tj;s[sj+1]=s[sj+1]-tj
例如:一开始数列s[]是0 0 0 0 0 0
3到5天需要2的教室,那么将s[3]+=2,s[5+1]-=2。
数列s[]变为:0 0 2 0 0 -2
前缀和数组为:0 0 2 2 2 0,这样就实现了增加3~5天需要的教室数,接下来二分订单数,处理前mid个订单看看是否有某一天的前缀和大于di。
1 #include<iostream>//时间复杂度:O(n+m) 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 int n,m,ans,a[1000010],d[1000010],x[1000010],y[1000010],s[1000010],sum; 6 template <class T> T get(T &u)//读入优化 7 { 8 char x; 9 for(;!isdigit(x=getchar());); 10 for(u=x-48;isdigit(x=getchar());u*=10,u+=(x-48)); 11 ungetc(x,stdin); 12 return u; 13 } 14 bool judge(int v) 15 { 16 memset(s,0,sizeof(s)); 17 sum=0;//初始化前缀和 18 for(int i=1;i<=v;i++)//令人窒息的操作 19 { 20 s[x[i]]+=d[i]; 21 s[y[i]+1]-=d[i]; 22 } 23 for(int i=1;i<=n;i++)//sum前缀和操作 24 { 25 sum+=s[i]; 26 if(sum>a[i]) return 0;//有某一天的前缀和大于di,返回0 27 } 28 return 1;//没有,返回1 29 } 30 int main() 31 { 32 get(n),get(m);//读入n,m 33 for(int i=1;i<=n;i++) get(a[i]);//读入原数据数组a[] 34 for(int i=1;i<=m;i++)//读入信息 35 get(d[i]),get(x[i]),get(y[i]); 36 int l=1,r=m;//二分初始化,左为1,右为订单数 37 while(l<=r) 38 { 39 int mid=(l+r)>>1; 40 if(!judge(mid)) 41 { 42 ans=mid; 43 r=mid-1; 44 } 45 else l=mid+1; 46 } 47 if(!ans) printf("0"); 48 else printf("-1\n%d",ans); 49 return 0; 50 }
代码来自:http://hzwer.com/2959.html
经典例题:乌龟棋(Luogu 1541 NOIP2010 D2T2)
乌龟棋的棋盘是一行 N 个格子,每个格子上一个分数(非负整数)。棋盘第 1 格是唯一的起点,第 N 格是终点,游戏要求玩家控制一个乌龟棋子从起点出发走到终点。
乌龟棋中 M 张爬行卡片,分成 4 种不同的类型( M 张卡片中不一定包含所有 4 种类型的卡片,见样例),每种类型的卡片上分别标有 1、 2、 3、4 四个数字之一,表示使用这种卡片后,乌龟棋子将向前爬行相应的格子数。游戏中,玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片,控制乌龟棋子前进相应的格子数,每张卡片只能使用一次。
游戏中,乌龟棋子自动获得起点格子的分数,并且在后续的爬行中每到达一个格子,就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。
- 棋盘: 6 10 14 2 8 8 18 5 17
- 卡片: 1 3 1 2 1
- 答案: 73 = 6+10+14+8+18+17
数据范围:1≤N≤350,1≤M≤120
算法描述:
很明显,用不同的爬行卡片使用顺序会使得最终游戏的得分不同,小明想要找到一种卡片使用顺序使得最终游戏得分最多。现在,告诉你棋盘上每个格子的分数和所有的爬行卡片,你能告诉小明,他最多能得到多少分吗?

* 思考:如何进行搜索?状态该如何设计?
* DFS(x,c1,c2,c3,c4) 为当前在第 x 个格子上, ci 代表标有数字i 的卡片有多少张。
* 于是可以直接写出状态 F[i][a][b][c][d],与状态是一一对应的,表示该状态下, 最大的权值是多少(当前第i个格子,四种牌分别用了i,j,k,l张的情况下,能达到的最优值)。
* 于是,可以和 F[i-1],F[i-2]…进行联系
1 //T27:乌龟棋(我把i省略了,其实没什么用,加上只是用来判断是否越界而已) 2 for(int i=0;i<=a;i++) 3 for(int j=0;j<=b;j++) 4 for(int k=0;k<=c;k++) 5 for(int l=0;l<=d;l++) 6 { 7 if(i!=0)f[i][j][k][l]=max(f[i][j][k][l],f[i-1][j][k][l]); 8 if(j!=0)f[i][j][k][l]=max(f[i][j][k][l],f[i][j-1][k][l]); 9 if(k!=0)f[i][j][k][l]=max(f[i][j][k][l],f[i][j][k-1][l]); 10 if(l!=0)f[i][j][k][l]=max(f[i][j][k][l],f[i][j][k][l-1]); 11 f[i][j][k][l]+=s[i+j*2+k*3+l*4]; 12 }
经典例题:运输计划(Luogu 2680 NOIP2015 D2T3)
问题简化:给定一棵有n个节点的带边权的树,以及m个条件ai,bi。可以将某一条边的边权变为0,目标使max{dis(ai,bi)}最小(所有路径费用的的最大值最小)。
数据范围:n,m≤300000。
算法描述:
我们可以换个角度思考:枚举答案x而不是删除某条边,答案显然可以二分!
对于所有长度超过x的条件,在树中将这些边标记,表示这些边中必须删除一条边,标记方法表示为:f[ai]++,f[bi]++,f[lca(ai,bi)]=f[lca(ai,bi)]-2;
最终被所有长度超过x的条件标记的边中找出最长的边,判断是否可行。
NOIP的时候,遇到一道题目是树剖→你想错了!
题目中要求“最大值最小”或“最小值最大”,95%是二分答案!
假如存在一种方案最大值不会超过x,那么必定存在一种方案最大值不会超过x+1。
假如不存在方案使得最大值不超过x,那么必定不存在方案使得最大值不超过x-1。
x满足连续性。
我们二分答案得到一个值mid(在最长链和最短链长度中二分出mid),判断是否存在一种方案(把一条边的边权变为0),使得所有链的长度都≤mid
如果说对于某一条链,它一开始的长度≤mid,合理!一开始的长度>mid,那么这一条链绝对存在一条边的边权变为0,执行m条即可。
这样,问题转化成:能否删除一条边,使得这m条链的链长长度都≤mid。
对于一条链,在树上标记下来,表示这些边必须得有一条被删掉,每条链都这么做。
如果一条边,被所有链都标记过,说明删掉这条边后可能能满足要求,假如说存在多条这样的边,肯定把最长的边的边权变为0,最后判断所有链是否都满足条件。
假设最长的链长度为=x,最长的满足条件的边的边权=y,只有当x-y≤mid时,满足条件。
标记方法:
对于一条链,在树上标记下来:一条链可以被分成两条链,其中每条链都满足两个端点u、v满足u是v的祖先,即:f[v]++,f[u]--;最后求以每个点为根的子树中f的和,就是它被标记的次数!
时间复杂度:O(nlgn)。
经典例题:华容道(Luogu 1979 NOIP2013 D2T3)
有一张n×m的图,其中有一些是障碍。
有q个询问,每个询问给定空白格子,初始格子,目标格子。
每次操作只能将空白格子与其相邻的非障碍格子交换位置,对于每次询问,输出要使初始格子到达目标格子的最小步数。
n,m<=30,q<=500;n,m<=30,q<=10(70分)。
解题过程:
一个比较暴力的做法:
对于每组询问,直接广搜BFS,令f[i][j][k][l]表示此时空白格子在(i,j),初始格子在(k,l)时的最小步数,每次相当于空白格子在走,转移比较简单。
时间复杂度为q×n2×m2。
另一个优化版的做法:
考虑初始格子移动的本质。
每当初始格子移动后,空白格子一定在它周围。
因此我们可以预处理出这么一个东西。
令dp[i][j][0/1/2/3][0/1/2/3]表示初始格子在(i,j),空白格子在其相邻的哪个方向,下一步该初始格子要走到相邻的哪个方向的最小步数。
其中每次询问都要先将空白格子移动到初始格子周围。
时间复杂度为n2×m2+shortest_path(n×m,n×m)×q。
经典例题:打怪兽(野题)
有n<=10W只怪兽,你可以随便选个顺序打过去,初始你有a滴血,打掉第i个怪兽会扣掉你bi滴血,扣完后会掉落一个血瓶,你可以回复ci点血,打完这n个怪兽后你才能去见BOSS。
当你血量<=0时你会挂掉。
问你能否见到BOSS,输出任意一种可行的方案。
解题思路:
按照一般的贪心思路,首先想到性价比什么的。。。但是发现这些都不对。。。
一种正确的贪心思路:“先吃饱再消化”,意思就是首先把怪兽分为两种,一种能给你加血(ci-bi≥0),另一种会扣你血(ci-bi<0)。
这样就变成了两个简单的问题:
加血的我们应该怎么打?——按伤害从小到大排序
会掉血的我们应该怎么打?——按加血量从大到小排序
假如,存在一只怪兽不加血,那么我们留到最后再打,例如下:
①初始血量:13 第一个怪兽血量:12 掉落血瓶:8;第二个怪兽血量:1 掉落血瓶:0
对于这样的情况,我们是先打第一只再打第二只。
①初始血量:15 第一个怪兽血量:13 掉落血瓶:0;第二个怪兽血量:2 掉落血瓶:1
对于这样的情况,我们是先打第二只再打第一只。
关于“打会掉血的怪兽,我们按照加血量从大到小排序”这种打法的证明:
每个数字都减去最小值和原问题等价,我们能确定最后打哪只怪兽。
对于剩下的n-1只怪兽,再都减去最小值,我们能确定倒数第二次打哪只怪兽。
同样对于剩下的n-2只怪兽……
如下面这种情况:
初始血量:15 第一个怪兽血量:14 掉落血瓶:10;第二个怪兽血量:3 掉落血瓶:2
肯定是先打第一只怪兽,然后打第二只怪兽。
15-14+10-3+2=10
15 =10-2+3-10+14(移项)
从上式我们就可以看出:对于会扣你血的怪兽,换个角度思考,从最后一只怪兽开始,回的血相当于扣的血,扣的血相当于回的血,此时和第一种情况是一样的。
因此按照加血量从大到小排序就可以了(理解:把等号左边的移动右边)
所以,在打会掉血的怪兽时,按照加血量从大到小排,这样打一定是最优的。
如果按照这种策略打不过了,实际上按照任何一种策略都打不过。
经典例题:销售比赛(野题)
有n天(n是偶数),第i天的物品价格为ai,每一天你可以选择买一件或者卖一件物品,并且必须选择。
初始时有花不完的钱,问n天后最多盈利多少钱。
解题思路:
首先需要明确的一点是,第一天肯定得买,最后一天肯定得卖,且最终所有物品都恰好卖完。
那么现在我们来看第二天和第三天的物品,肯定拿价格大的卖,价格小的买(不考虑同时买)。
接下来的每两天中,若价格小的那个价格都比之前卖出的物品价格高,则将之前的那个物品买进,这个物品卖出。
这个贪心显然是正确的(验证一下真的很“显然”)。
经典例题:残缺方块问题(野题)
有一个2k×2k的棋盘,其中恰好有一个方块残缺。以下是k=1时的4种情况。
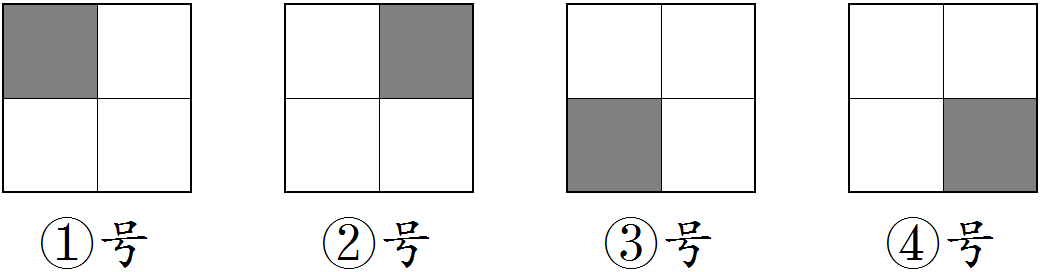
我们需要通过若干三格板(可旋转)来覆盖这个棋盘,要求任意两块三格板不重叠,且三格板不覆盖残缺的方块。输出一种方案即可。
解题思路:
考虑分治算法,将一个k=i的问题转化为4个k=i-1的子问题,如下图:
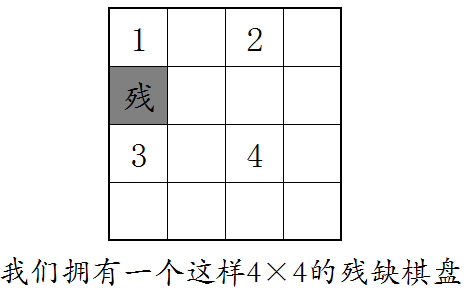
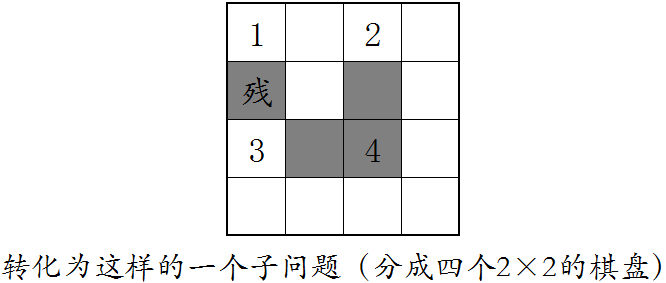
其中每一部分均变成了一个子问题,而我们知道k=1时可以直接构造,如此分治即可。
四、ZHW最后的吹水:
1.NOIP洛谷上刷满500题,提高组一等奖没问题。。
2.对数字要有敏感,例如:
128M=134217728Byte
=(134217728/8)个long long类型数据
=(134217728/4)个int类型数据
=(134217728/2)个short类型数据
=(134217728/1)个bool、char类型数据
3.平时写题多写写对拍,试一下大数据和比较***难的数据。
4.刷题,历年NOIP都可以拿到400分,就很稳;保证一等奖的话,至少350分。
5.信息学奥赛和我们的数学英语不一样,你随便乱选几个,都可以拿到十几二十分这样,但在OI中,呵呵,爆内存的话100分直接变成0分!
6道题,7个小时,难度较高,要做到,在平时的比赛,碾压别人!
6.辣鸡的做题顺序:看到一道题→想了一会儿不会做→网上找题解→会做了→懒得做了→copy一下交上去→炉石!
7.对题目中数据的范围要有敏感,例如:
N=100w,O(n) N=10w,O(nlgn)或O(nlg2n)
N=30w,O(nlgn) N=5w,O(n×sqrt(n))
N=5000,O(n2) N=300,O(n3)
N=1000,O(n2×lgn) N=100,O(n4)
N=40,O(2(n/2)×n) N=35,O(2(n/2)×n×lg)
N=20,O(2n×n) N=10,O(n!)
最近发现一些网站盗用我的blog,这实在不能忍(™把关于我的名字什么的全部删去只保留文本啥意思。。)!!希望各位转载引用时请注明出处,谢谢配合噢~




