2017清北学堂(提高组精英班)集训笔记——基本数论
这是一个很大的专题同时也很重要,所以我十分再十分仔细地写这个笔记,所以有点慢大家别介意。废话不多说进入正题!
一、数论(研究整数性质的东西):
1.数论的分类(来自百度百科):
初等数论、解析数论、代数数论、几何数论、计算数论、超越数论、组合数论、算术代数数论。
2.数:
整数、自然数(大于等于0的整数)、正整数(大于0的整数)、负整数、非负整数、非正整数、非零整数、奇数 偶数。
3.Problem 3:
设N为奇数,a1,a2,…,aN为1,2,…,N的一个排列,求证:(a1-1)(a2-2)…(aN-N)≡0(mod 2)。
证明:因为a1,a2,…,aN为1,2,…,N的一个排列,所以a1+a2+…+aN=1+2+…+N,移项,得:(a1-1)+(a2-2)+…+(an-N)=0为偶数,所以(a1-1),(a2-2),…,(an-N)中必定有至少一项为偶数,所以(a1-1)(a2-2)…(an-N)为偶数,即:(a1-1)(a2-2)…(aN-N)≡0(mod 2)。
4.整除性:
设a,b∈Z,如果存在c∈Z并且a=bc,则称b|a(b为a的因子,“|”表示“能整除”)
5.质数:
如果一个数,只有1和自身作为因子的数,叫做质数(素数)。
通论1:存在一个质数p,若p|ab,则p|a或者p|b。
通论2:若p|a或者(p,a)=1(p和a的最大公因子为1),则p|a2 可以推出 p|a。
通论3:用π(x)表示不超过x的质数的个数,可以证:limπ(x)lnx÷x=1,换种通俗说法就是:1~x的质数个数大约为x/lnx(证明时间复杂度时可以用)。
6.Problem 3.141:
求证:当n为合数时,2n-1为合数。
证明:因为n为合数,我们可以令n=ab,则2n-1=(2a-1)·(2n-a+2n-2a+2n-3a+…+2a+1),原式得证。
还可以看出平方差公式是这个的一个特例。
7.质数的判定:
(1)一个很多人都在用的办法(判断一个较小的数是否为质数):
1 bool prime(int x)//判断质数 时间复杂度:O(sqrt(x)),最多1012~1014 2 { 3 if(x<2) return false; 4 for(int a=2;a*a<=x;a++) 5 { 6 if(x%a==0) return false;//不是质数 7 } 8 return true;//是质数 9 }
(2)运用费马小定理:
p为一个素数且p不是a的倍数,则有:ap-1≡1(mod p)(不能从右边推到左边)
做法:多次选取a检验p是否满足费马小定理(说明p可能是质数,选的满足条件的a越多,p为质数的可能性越大)。
时间复杂度为:O(klogp),选取k个a,判断的过程用掉logp,总的加起来为klogp。
特别地,这样的算法有缺陷,因为有Carmichael数的存在,可导致上述算法给出一个错误的判断,例如:561、1105、1729,这三个数满足费马小定理,但是它们都是合数!
这里给出1~10000的Carmichael数:561、1105、1729、2465、2821、6601、8911。
(3)Miller-Rabin算法(判断一个很大的数是否为质数):
由于Carmichael数的存在,并且Carmichael数是有无穷多个的,那怎么办?打表?肯定不行啊!所以就要加强这个算法!
如果n为素数,取a<n,令n-1=d×2r,则要么ad≡1(mod n),要么存在一个数i满足:0≤i<r,使得:ad×2^i≡-1(mod n),“一个数mod n=-1”可以表示为:“一个数mod n=n-1”,同样地也是不能从右边推到左边。
时间复杂度:O(klogn)
做法:多次选取a检验p是否满足,则是质数的概率就大。(有个好消息:不存在Carmichael数这样的特殊情况!)
例如:12=3*22
1 int a[5]={3,7,11,23,37}//这里选了钟神喜欢的5个质数来检验是否满足条件,如果不够保险的话还可以多加几个 2 bool Miller_Rabin(int n)//从a[]中选出5个a 3 { 4 n-1=d*2^r;//用n-1来确定d、r 5 for(int j=1;j<=5;j++)//这里用了5个小于n的质数a来检验,用质数是因为效果更好! 6 { 7 if(pow(a[j],d)%n!=1)//不满足第一个条件,pow为快速幂函数,pow(a,b)计算a^b 8 { 9 for(int i=0;i<r;i++) 10 { 11 if(pow(a[j],d*2^i)%n==-1) return true;//第二个条件 12 } 13 return false; 14 } 15 } 16 }
(4)筛法(处理1~n区间内有哪些质数):
基本做法:给出要筛数值的范围sqrt(n),找出 sqrt(n)以内的素数p1,p2,p3,…,pk。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个素数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个素数5筛,把5留下,把5的倍数剔除掉;这样不断重复下去……
①非线性筛法;
1 bool not_prime[1000000];//true表示不是质数,false表示是质数 2 not_prime[1]=true;//1不是质数 3 for(int a=2;a<=n;a++) 4 { 5 for(int b=a+a;b<=n;b+=a) 6 { 7 not_prime[b]=true; 8 } 9 }
时间复杂度:(1/1+1/2+1/3+1/4+…+1/n)*n=nlogn
下面给出了优化版筛法,时间复杂度为:nlog(logn)
算法思路:如果当前这个数是合数,之前已经枚举过比它小的因子,在枚举这个小因子的时候,已经把这个合数的倍数覆盖掉了,所以没必要。
1 bool not_prime[1000000];//优化版非线性筛法 2 not_prime[1]=true;//1不是质数 3 for(int a=2;a<=n;a++) 4 { 5 if(!not_prime[a])//如果是质数,进入循环,是合数就不进入 6 { 7 for(int b=a+a;b<=n;b+=a) 8 { 9 not_prime[b]=true; 10 } 11 } 12 }
②线性筛法:
算法思路:每个合数都由它最小的质因子筛掉(代码第12行)。一个合数会被拆成几个质因子相乘,利用最小的质因子就可以把这个合数筛掉了,避免了重复筛的过程。
1 int not_prime[1000000]; 2 int prime[1000000];//质数表 3 int prime_count=0;//质数的个数 4 memset(not_prime,0,sizeof(not_prime)); 5 not_prime[1]=true;//1不是质数 6 for(int i=2;i<=n;i++) 7 { 8 if(!not_prime[i]) prime[++prime_count]=i;//把i放入质数表prime[]中 9 for(int j=1;j<=prime_count;++j)//枚举质数表中的每一个数 10 { 11 if(prime[j]*i>n) break; 12 not_prime[prime[j]*i]=true;//翻倍,一个数×另一个数一定为合数 13 if(i%prime[j]==0) break; 14 } 15 }
时间复杂度:是线性的,接近于O(n)。
8.最大公因数:
(1)欧几里得算法(辗转相除法):
原理什么的我就不说了,看代码YY一下就知道啦(详见人教版高中数学必修三)。
1 int gcd(int a,int b)//欧几里得算法 时间复杂度:O(loga) 2 { 3 if(!b) return a; 4 else return gcd(b,a%b); 5 } 6 int gcd(int a,int b)//简化版欧几里得算法 时间复杂度:O(loga) 7 { 8 return b?gcd(b,a%b):a;//一行代码就是爽 9 }
(2)扩展欧几里得算法:
用来在已知的a、b中求解一组x、y,使得ax+by=gcd(a,b)成立(根据数论相关定理,这组解一定存在)
求解过程(引自P2O5 dalao的blog:http://p2oileen.xyz/index.php/2017/06/07/exgcd/):
设a>b,则有当b=0时,gcd(a,b)=a,此时x=1,y=0。
当ab≠0时,设ax1+by1=gcd(a,b),因为gcd(a,b)=gcd(b,a%b),则一定有:bx2(a%b)y2=gcd(b,a%b)=gcd(a,b)=ax1+by1
所以将bx2+(a%b)y2=ax1+by1移项+整理可得:
ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
根据恒等定理:x1=y2; y1=x2-(a/b)*y2;
这样我们就可以通过x2,y2递归求解x1,y1辣!
在gcd不断递归求解的过程中,总会有一个时刻b=0,所以递归是有终止条件的。
递归代码如下:
1 int Ex_Gcd(int a,int b,int &x,int &y) 2 { 3 if(b==0) 4 { 5 x=1; 6 y=0; 7 return a; 8 } 9 int ans=Ex_Gcd(b,a%b,x,y); 10 int t=x; 11 x=y; 12 y=t-a/b*y; 13 return ans;//返回a、b的最大公约数 14 }
9.中国剩余定理(求解一次同余式组):
原问题:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
简单地来说:有一个数x≡a1(mod p1),x≡a2(mod p2),x≡a3(mod p3),…,x≡ak(mod pk),求解一个最小的x。
根据问题,我们可以得出好多好多好多的方程:
x=k1p1+a1;x=k2p2+a2;……
两个方程为一组,解之:
k1p1+a1=k2p2+a2移项得:k1p1-k2p2=a2-a1;
在我们小学的时候,就接触了一个这样的解法,很简单很实用,现在就来模拟一下!
大数翻倍法(一种求解最小公倍数的方法):
举个栗子:
1 //大数翻倍法 时间复杂度:O(min(p1,p2)) 2 int fanbei(int a1,int p1,int a2,int p2)//p1<p2 3 { 4 ans=a2; 5 while(ans%p1!=a1) ans=ans+p2; 6 return ans; 7 }
根据ans=a2+p1p2≡a2(mod p1),计算得出时间复杂度为O(min(p1,p2)),也就是说加p1次一定会找到一个解!
10.逆元:
定义:如果gcd(a,m)=1且存在唯一的b使得a×b≡1(mod m)且1≤b<m,则b为a在模m意义下的逆元,a、b互为逆元。
举个栗子:令a=3,m=7,我们希望找到一个b满足a×b≡1(mod m)且1≤b<m,不难找到b=5。则5为3在模7意义下的逆元,3、5互为逆元。
逆元的作用:在模的意义下做除法,举个栗子:计算(3×6÷3)mod7的结果,按照一般的顺序可以算出原式=(18÷3)mod7=6mod7=6。我们利用模的性质,可以把原式变为:(((3×6)mod7)÷3)mod7=4÷3mod7。我们发现进行到这里就无法计算了(模意义下不能做除法),这时候就要用到逆元,3的逆元为5,所以原式"4÷3mod7"变为"4×5mod7",计算得6。
寻找逆元的方法:
①费马小定理:ap-1≡1(mod p),p为质数,求a的逆元(保证a和p互质)?
两边同除以a得:ap-2≡1/a(mod p),也就是说,任意一个数a在模质数p意义下的逆元就是ap-2。
②欧拉定理:aφ(m)≡1适用于任何数m,但要保证gcd(a,m)=1,解法和费马小定理相同,φ(m)的意义之后会讲。
11.积性函数:
定义:如果对于gcd(n,m)=1,有f(nm)=f(n)f(m),则称f为积性函数,例如f(x)=1就是积性函数。
给出一些经典的积性函数:
①σ(n)=Σd|nd:n的所有因子之和
②τ(n)=Σd|n1:n的因子个数
③μ(n)莫比乌斯函数,稍后会讲(详见13点)
④φ(n)欧拉函数:1~n当中与n互质的数的个数,例如φ(6)=2,下面介绍用大约O(n2)的方法求1~n的所有数的φ(ai):
假设一个数n,求φ(n)?因为n=P1k1·P2k2·…·Prkr → φ(n)=n·(P1-1)/P1·(P2-1)/P2·…·(Pr-1)/Pr。
举两个例子:
30=2*3*5,所以φ(30)=30*(1/2)*(2/3)*(4/5)=8。
160=25*5,所以φ(160)=160*(1/2)*(4/5)=64。
讲了这么多的函数,怎么样用到积性的性质呢?
积性的意义在于:可以在O(n)的时间复杂度内,求出1~n所有数的函数值。
如下的例子(运用在欧拉函数):我们在O(n)的时间内求出1~n所有数的φ值
要用到线性筛(其他的函数也是差不多——线性筛中加上函数即可)!
1 memset(notprime,0,sizeof(notprime)),notprime[1]=true;//初始化 2 phi[1]=1;//赋初值,φ(1)=1 3 for(int i=2;i<=n;i++) 4 { 5 if(!notprime[i])//是质数 6 { 7 prime[++prime_count]=i; 8 phi[i]=i-1;//如果i是质数,显然和i互质的数有i-1个 9 } 10 for(int j=1;j<=prime_count;++j)//求合数的φ 11 { 12 if(prime[j]*i>n)//考虑prime[j]*i这个合数 13 { 14 break; 15 } 16 not_prime[prime[j]*i]=true; 17 /*根据积性函数定义,有φ(prime[j]*i)=φ(prime[j])*φ(i),要用积性函数的性质,必须满足prime[j]和i互质*/ 18 if(i%prime[j]!=0)//prime[j]和i互质 19 { 20 phi[prime[j]*i]=phi[prime[j]]*phi[i];//直接利用积性函数性质 21 } 22 else//i是prime[j]的倍数(不互质) 23 { 24 phi[prime[j]*i]=prime[j]*phi[i]; 25 /*把prime[j]*i分成prime[j]段,每段长度为i,那么每一段与i互质的数一样多,根据性质:若a与b互质,那么a+b与b互质,a+2b与b互质,所以在第一段和i互质的数加上i之后还和prime[j]互质,所以整个里面就有prime[j]*phi[i]个数和它是互质的,所以phi[prime[j]*i]=prime[j]*phi[i]*/ 26 } 27 if(i%prime[j]==0) break; 28 } 29 }
12.卷积(这个我是真的不懂):
f*g=Σd|nf(d)g (n/d)
13.莫比乌斯:
(1)莫比乌斯函数:
含义(三种情况):拆解一个数n=P1k1*P2k2*P3k3*…*Prkr
①若n=1,μ(n)=1 ②当k1=k2=k3=…kr=1时,μ(n)=(-1)r ③前面两个条件都不满足时,μ(n)=0。
意义:容斥原理必备,多有使用到的地方,希望考虑一下吧。
(2)莫比乌斯反演:
以下两个条件等价:
①对于任意正整数n,f(n)=Σd|ng(d)
②对于任意正整数n,g(n)=Σd|nμ(d)f(n/d)
14.一些东西:
①Σd|nφ(d)=n:一个数的因子的φ加起来等于n。
②Σd|nμ(d)=[n=1]:如果n=1,则n的所有因子的μ值和为1,否则为0。
15.欧拉定理:
费马小定理的推广:aφ(m)≡1(mod m)。
补充一些同余的性质:
①反身性:a≡a(mod m)
②对称性:若a≡b(mod m),则b≡a(mod m)
③传递性:若a≡b(mod m),b≡c(mod m),则a≡c(mod m)
④同余式相加:若a≡b(mod m),c≡d(mod m),则a±c≡b±d(mod m)
⑤同余式相乘:若a≡b(mod m),c≡d(mod m),则ac≡bd(mod m)
经典例题:给定数a、b、p,求ax≡b(mod p)的最小正整数解x。
BSGS算法——“北上广深算法”或“拔山盖世算法”:
令x=im-j,m=⌈sqrt(p)⌉,则aim-j≡b(mod p),
移项,有:(am)i≡baj(mod p)
首先,从0~m枚举j,将得到的baj的值存入hash表;
然后,从1~m枚举i,计算(am)j,查表,如果有值与之相等,则当时得到的im-j是最小值。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<map> 6 #include<cmath> 7 using namespace std; 8 long long a,b,c,m,f[10000000]; 9 map<long long,int> mp; 10 long long qsm(long long x) //快速幂 11 { 12 long long sum=1; 13 long long aa=a; 14 while(x>0) 15 { 16 if(x&1) 17 sum=(sum*aa)%c; 18 x=x>>1; 19 aa=(aa*aa)%c; 20 } 21 return sum; 22 } 23 int main() 24 { 25 mp.clear();//删除map中的所有元素。 26 while(scanf("%lld%lld%lld",&c,&a,&b)!=EOF) 27 { 28 mp.clear(); 29 if(a%c==0)//判断a,c 是否互质,因为c 是质数,所以直接判断是否整除即可 30 { 31 printf("no solution\n"); 32 continue; 33 } 34 int p=false; 35 m=ceil(sqrt(c)); 36 long long ans; 37 for(int i=0;i<=m;i++) 38 { 39 if(i==0) 40 { 41 ans=b%c; 42 mp[ans]=i; 43 continue; 44 } 45 ans=(ans*a)%c; 46 mp[ans]=i; 47 } 48 long long t=qsm(m); 49 ans=1; 50 for(int i=1;i<=m;i++) 51 { 52 ans=(ans*t)%c; 53 if(mp[ans]) 54 { 55 int t=i*m-mp[ans]; 56 printf("%d\n",(t%c+c)%c); 57 p=true; 58 break; 59 } 60 } 61 if(!p) 62 { 63 printf("no solution\n"); 64 } 65 } 66 }
经典例题:求[l,r]之间的所有素数,1≤l≤r≤109,r-l≤105。
三个解法:
①Miller-Rabin
②线性筛
③SPOJ PRIME1
二、概率:
一些定义和推论:
①Pr[i]表示事件i发生的概率
②Pr[1]+Pr[2]+…Pr[N]=1
③xi表示事件i的权重(自己定义的权重)
④事件xi的期望E[xi]=Pr[i]×xi(i:1~N) 期望=概率×权重
⑤对于独立事件i和j,Pr[i^j]=Pr[i]×Pr[j],事件i和j的期望是可加的
⑥当事件j已经发生时,事件i发生的概率为:Pr[i|j]=Pr[i^j]/Pr[j]
一个有趣的结论:当太阳已经从东边升起N天后,第N+1天从东边升起的概率:(N+1)/(N+2)。
1.Problem 1:
在小葱和小泽面前有三瓶药,其中有两瓶是毒药一瓶是可乐,每个人必须喝一瓶。
小葱和小泽各自选了一瓶药,小泽手速比较快将药喝了下去,然后就挂掉了。
小葱想活下去,他是应该喝掉手上这瓶药,还是喝掉另外一瓶呢?
我们把瓶子编号为1、2、3,1、2号药是毒药,3号药是可乐。
根据全排列的知识,我们列出6种情况:
1、2、3;1、3、2;
2、1、3;2、3、1;
3、1、2;3、2、1;
由于第一个人是被毒死了,所以只可能是1、2、3;1、3、2;2、1、3;2、3、1;这四种情况,我们发现第二个人喝的是解药的概率为:Pr[是解药]=(1+1)/4=50%。
更简单的想法:小葱选哪个都一样,因为小葱不知道哪个是毒药哪个是可乐。
钟神:显然无所谓!
2.浅谈玛丽莲问题:
美国某娱乐节目的舞台上,台上有三个门,其中一个门后边有汽车,另外两个门后边是山羊,主持人让你任意选择其中一个,然后他打开其余两个门中的一个,你看到的是山羊,这时,主持人会让你重新选择,那么你会坚持原来的选择还是换选另外一个未被打开过的门呢?
分两种情况讨论:
①不换门:抽中汽车的概率是1/3。
②换门:我们编号三个门分别为1、2、3,分别对应羊、羊、车
情况1:假设你第一次猜的那个门是1,主持人必将打开2,选择换门3必能得到车。
情况2:假设你第一次猜的那个门是2,主持人必将打开1,选择换门3必能得到车。
情况3:假设你第一次猜的那个门是3,主持人会打开1或2,你会换1或2号门,得不到车。
综上所述:换门抽中汽车的概率为2/3。
Pr(换门)>Pr(不换门),所以应该换门!
现在思考:同样是二选一,为什么概率会不同?
因为主持人知道哪个门是羊哪个门是车,上一题中小葱不知道哪瓶是毒药,因为主持人从中作祟,所以概率不同!
3.Problem 2:
小胡站在原点,手里拿着两枚硬币。抛第一枚硬币正面向上的概率为p,第二枚正面向上的概率为q。
小胡开始抛第一枚硬币,每次抛到反面小胡就向x轴正方向走一步,直到抛到正面。
接下来小胡继续抛第一枚硬币,每次抛到反面小胡就向y轴正方向走一步,直到抛到正面。
现在小胡想回来了,于是他开始抛第二枚硬币,如果小胡抛到正面就向x轴的负方向走一步,否则小胡就向y轴的负方向走一步。
现在小胡想知道他在往回走的时候经过原点的概率是多少?
根据定理:往x轴走k步的概率为(1-p)x×p,同理于y轴。
我们可以枚举小胡在第一轮中走到的点(x,y)
小胡走到点(x,y)的概率为(1-p)x+y×p2(乘法原理)
小胡从点(x,y)走回原点的概率为qx×(1-q)y×[(x+y)!/(x!×y!)]。
说明:qx×(1-q)y表示前几步都走x步,后几步都走y步的概率,而实际情况是可以交替着走的,所以我们在后面乘上(也就是[(x+y)!/(x!×y!)]),才能表示从两种情况中选择往x、y之一走的概率。
所以最终的概率为(对所有情况进行求和):
这个式子很不好求啊!!肆意展示一下数学功底的时候到了!
我们改变枚举量进行化简!过程如下:
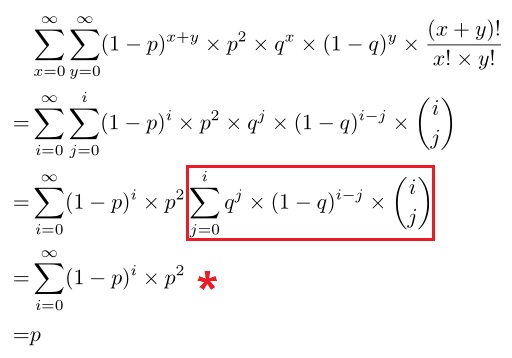
其中:
说明:在以上的推理过程中,打"*"的这一步和红框的推理过程:
①打红框这一步推理:
根据二项式定理,有(字丑不要介意;′⌒`):
类比一下,有a=q,b=(1-q),所以原式可以化简为(q+1-q)i=1i=1(太™聪明了啊!!)
②打"*"这一步推理:
直接是等比数列求和即可!
4.Problem 2.333333:
小葱想要过河,过河有两条路:
一条路有100个石头,每个石头有1/100的概率会挂掉。
另一条路有1000个石头,每个石头有1/1000的概率会挂掉。
小葱应该走哪条路呢?(请勿使用计算器)
5.Problem 3(这道题太丑被丢掉了):
小葱在平面上画了很多条平行等间距为l的直线,小葱将长度为1的针投到这个平面上,求针和直线相交的概率?
典型的蒲丰投针问题:
分情况讨论:
①当l≤1:
②当l>1:
6.Problem 4:
小泽在数轴上的0点处,他每次有r的概率向右走,有1-r的概率向左走,求小泽走到-1处的概率为?
解法:如果直接列式求和计算:大量组合数求和!卡特兰数!级数!(mmp看得我想死)
设到达x-1的概率为p,则p=(1-r)×1+r×p×p 第一步向左走到-1的概率+第一步向右走回到-1的概率(往左走两次到-1)
根据上式,变形得:rp2-p+1-r=0,解方程可得到:p=(1±|2r-1|)/2r,因为有绝对值,所以分类讨论2r和1的关系:
经过紧张又激烈的讨论,我们得出一个分段函数(r都可以取):
7.Problem 5:
小胡有一棵一个点的树,小胡会给这个点浇水,于是这个点会有𝑝的概率长出两个儿子节点。
每次长出新的节点之后,小胡又会给新的节点浇水,它们也都有𝑝的概率长出两个新的儿子节点。
小胡不希望自己被累死,所以小胡希望知道这棵树的大小是有限的的概率。
解法:这道题和上一题是一毛一样的!
8.经典题1:
给出n行m列矩阵,k次操作,每次操作选取一个子矩阵,子矩阵内的所有矩阵标记,做了k次操作内,被重复标记的标记为已标记。
求:k次操作后,对于左上角坐标为(x,y)的矩形,至少被1个子矩阵包含的概率为多少?
例如:下面一个2×2的矩阵:

当k=1时,有9种标记方法:
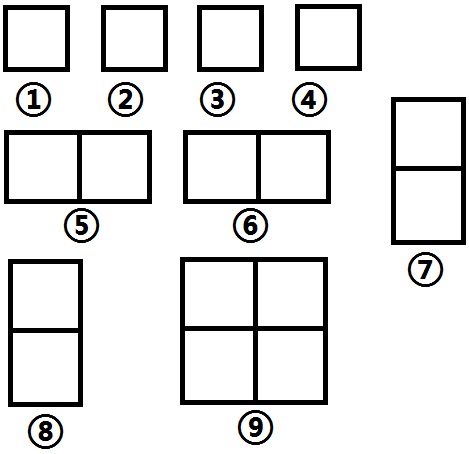
而我们总共能够标记1×4+2×4+4×1个矩阵,所以得到的概率为1/9×(1×4+2×4+4×1)=16/9。
推理过程:
假设k=1时,我们来观察一个3×4的矩阵:
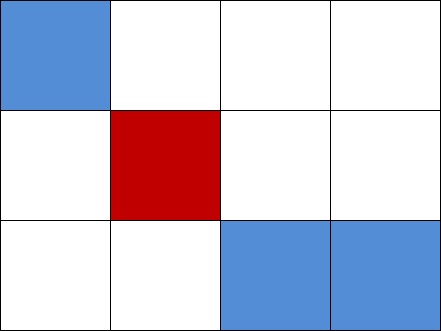
要使得A包含这个红色的矩阵B,那么这个矩阵A的左上点和右下点应该在蓝色的区域,这样才能保证完全覆盖红色矩阵。
假设这个矩阵的左上的点为(x,y),右下的点为(n-x+1,m-y+1),在这个图形里面总共有:(1+2+3+…+n)=[n×(n+1)×m×(m+1)]/(2×2)个矩阵,并且满足蓝色文字的条件后,矩阵一共有:x×y×(n-x+1)×(m-y+1)个,所以概率为:x×y×(n-x+1)×(m-y+1)/{[n×(n+1)×m×(m+1)]/(2×2)}。
9.经典题2:
有n个点,坐标为(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),求一个圆,包含这所有的点,并且保证半径最小。
暴力解法:枚举三个点,算出圆,把剩下的点全部丢进去判断在不在里面,算法复杂度:O(n4)
优化暴力解法O(n3):
1 for(int a=1;a<=n;a++)//往已知圆内一个一个地丢点 2 { 3 if(!in(p[a])) circle=cir(p[a]);//a不在圆内 4 circle=cir(p[a]);//构造以a位圆心的圆 5 for(int b=1;b<=a;b++) 6 { 7 if(!in(p[b])) circle=cir(p[a],p[b]);//构造以a、b两点为直径的圆 8 for(int c=1;c<=b;c++) 9 { 10 if(!in(c)) circle=cir(p[a],p[b],p[c]);//构造a、b、c三点共圆的圆 11 } 12 } 13 }
最优雅地优化O(n):利用C++中的一个函数叫:random_shuffle(随机打乱n个点的顺序),可以将时间复杂度优化到O(n),怎么样?很神奇很诡异吧??!
思想就是:随机选三个点形成一个圆,于是接下来的那些的点进入下面两个for循环的概率实际上很小!
三、代数:
来一些概念!代数的重要性…
最强大的计算工具
最基本的数学知识
近世代数的贡献
三大不可尺规作图问题
五次及以上的方程没有根式解
同构问题的计数
近代以及现代的加密技术
1.排列和逆序对:
排列的定义:一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列,当n=m时,这个排列被称作全排列。
逆序对的定义:τ,设A为一个有n个数字的有序集(n>1),其中所有数字各不相同,如果存在正整数i,j 使得1≤i<j≤n并且A[i] >A[j],则<A[i],A[j]>这个有序对称为A的一个逆序对,也称作逆序数。例如τ(3,1,2)=2。
对换的定义:在一个排列中,对换其中某两个数,其余的数不动,得到另一个排列,这种操作称为一个对换。
奇偶排列的定义:如果一个排列的逆序数是偶数,则称此排列为偶排列,否则称为奇排列。
定理:对换改变排列的奇偶性。
定理:在全部的n阶(n≥2)排列中,奇偶排列各占一半。
定理:任意一个排列可经过一系列对换变成自然排列,并且所作对换次数的奇偶性与这个排列的奇偶性相同。
2.行列式(我不知道这玩意儿怎么用):
定义:N阶行列式是由N2个数aij(i,j=1,2,…,n)通过下式确定的一个数
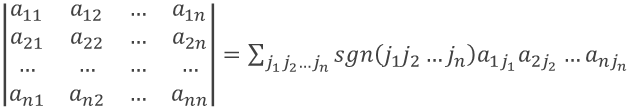
也称为行列式的完全展开式。
sgn(j1j2…jn)=(-1)τ(j1j2…jn)=![]()
一些引理:
①行列互换,值不变。
②用一个数乘行列式的某行等于用这个数乘此行列式。
③如果行列式中某一行是两组数之和,则这个行列式等于两个行列式之和,这两个行列式分别以这两组数为该行,而其余各行与原行列式对应各行相同。
④对换行列式中两行的位置,行列式为反号。
⑤如果行列式中有两行成比例,则行列式等于0。
⑥把一行的某个倍数加到另一行,行列式的值不变。
3.Cramer法则:
如果线性方程组:
则线性方程组有唯一解xj=Dj÷D(j=1,2,…,n)。
其中:
证明思路:先证明是解,再证明唯一性。
引理:
①若齐次线性方程组:
则方程只有零解。
②如果齐次线性方程组有非零解,则系数行列式必为零。
4.一般线性方程组:
定义①:一般线性方程组:
定义②:方程组的全体解称为方程组的解集合。
定义③:两个有相同解集合的方程组称为同解方程组。
定义④:线性方程组的初等变换(把一个方程组变为同解方程组):
<1>用一个非零数乘以某个方程。
<2>将一个方程的k倍加到另一个方程上。
<3>交换两个方程的位置。
定义⑤:系数矩阵:
定义⑥:增广矩阵:
定理:对n元非齐次线性方程组的增广矩阵实行高斯消元法,得到阶梯型矩阵:
5.高斯消元法:
思想:变成上三角矩阵!
如果dr+1≠0,方程组无解。
如果dr+1=0,方程组有解。
当r=n时,有唯一解。
当r<n时,有无穷多解。
高斯消元法举例详解:
我们先来看一个例子:
一个方程组:
运用高斯消元,把未知数前的系数和常数列出n×(n+1)的矩阵如下:
我们按照一般的解方程思路,肯定先想到消去x1,即②-①,③-①得:
然后再消去x2,即:③-②×3得:
然后我们保留除最后一列前面的矩阵:
这时,我们得到了一个上三角矩阵(说明有解,若不能化为上三角矩阵,则无解)!我们就可以直接用高斯消元。
∴观察得到的矩阵:x3=21/2,x2=3-2x3=-18,带入x3、x2即可求解得x1。
一个小小的问题:我们一直没有用到最后一列,那要算这一列干啥呢?这是用来方便计算答案的,也就是在构成上三角矩阵后直接利用最后一列的值计算即可(也就是下划线那步)。
再来看一个特例方程组:
按照上题的步骤,我们得到一个矩阵:
观察第一行,第一个数是0,不方便消元,所以我们往下找行,直到找到第一个数不是0为止,然后交换这两行,之后我们就可以开始消元了。
注意:对于第一个例子中的蓝色的"3“怎么得?我们是这样理解的:其实上面的运算"②-①","③-①"中,省略了"×1"这个项。我们假设后面的这个项是a,那么a=m[b][a]/m[a][a](m为矩阵),意思是第b个方程的xa的系数÷第a个方程的xa的系数。
要变成上三角矩阵,就要化简,我们用作为例子,要保证第一行前面0个0,第二行前面有1个0,第三行前面有2个0,以此类推…,所以我们用这行第一个不是0的数÷第一行这一列的数得到这个项即可得到a。
高斯消元代码(修改版,引用自P2O5 dalao:https://zybuluo.com/P2Oileen/note/816892#%E8%A1%8C%E5%88%97%E5%BC%8F):
1 void gauss()//时间复杂度:O(n^3) 2 { 3 //矩阵:m 4 for(int a=1;a<=n;a++) 5 { 6 if(fabs(m[a][a])<=eps) 7 { 8 for(int b=a+1;b<=n;b++)//eps=10^-9 9 { 10 if(fabs(m[b][a])>eps) swap(m[a],m[b]);//fabs用于浮点数,m[a],m[b]是引用//此处有问题,请大佬指正 11 break; 12 } 13 } 14 for(int b=a+1;b<=n;b++) 15 { 16 ratio=m[b][a]/m[a][a]; 17 for(int c=1;c<=n+1;c++)//c可以从a开始循环 18 { 19 m[b][c]-=m[a][c]*ratio; 20 } 21 } 22 } 23 for(int a=n;a>=1;a--) 24 { 25 solution[a]=m[a][n+1]; 26 for(int b=a+1;b<=n;b++) 27 { 28 solution/=m[a][a]; 29 } 30 } 31 }
举个栗子:
f(x)=ax5+bx4+cx3+dx2+ex+f
可以得到f(1),f(2),f(3),f(4),f(5),f(6),然后利用高斯消元法就可以解决这个问题了。
高斯消元法自动找规律机:
(1)用高斯消元法打表。
(2)枚举次数,符合表就是正确答案。
6.矩阵:
定义:由mn个数排列成m行n列矩阵的数表
称为一个m×n的矩阵,记做A。其中aij称为第i行第j列的元素。
一些特殊的矩阵种类:
①零矩阵0:所有元素都是0的矩阵。
②对角矩阵:主对角线(左上到右下)以外的数都为0的矩阵。
③单位矩阵I:矩阵对角线上都是1,其余为0。
④纯量矩阵:A=diag(c,c,…,c)。
⑤上三角矩阵:上半部分有值,例如:
⑥下三角矩阵:下半部分有值,例如:
⑦对称矩阵,例如:
⑧反对称矩阵
一些定义:
矩阵的相等:每个位置上的数相等。
矩阵的加法:两个矩阵对应位置元素相加。
矩阵的数量乘法:一个数乘以一个矩阵,矩阵中的每个元素都和这个元素相乘。
矩阵的乘法:设矩阵A=(aij)m×r,矩阵B=(bij)r×n,则矩阵C=(cij)m×n,其中cij=ai1b1j+ai2b2j+…+airbrj。
称为A与B的乘积,记做C=AB。
这里上个代码:
1 for(int a=1;a<=m;a++) 2 { 3 for(int b=1;b<=r;b++) 4 { 5 for(int c=1;c<=n;c++) 6 { 7 m3[a][c]+=m1[a][b]*m2[b][c]; 8 } 9 } 10 }
举个栗子:
和菲波那契的关系:
[fn-1 fn]×=[fn fn+fn-1]=[fn fn+1]
所以我们要计算[0 1]的斐波那契数列,只要不断地×即可=[fn fn+1]。
特别地,矩阵乘法没有交换律:AB≠BA!
我们还可以结合快速幂进行斐波那契的计算,例如:[0 1]×11,可以进行如下变换:把
11的指数11拆成8+2+1,即为23+21+20,然后运用快速幂把这些乘起来即可。
一个小小的问题:这个是怎么推出来的呢?
我们假设有方程f(n)=af(n-1)+bf(n-2),所以斐波那契就是当a=b=1时的特殊情况,根据矩阵乘法,我们假设这个矩阵为[ ],并且这个矩阵肯定是2×2的,所以有:[fn fn-1]×=[fn+1 fn]。所以有fn+1=wfn+yfn-1,fn=xfn+zfn-1,所以:fn+1=afn+bfn-1,fn+1=wfn+yfn-1,→a=w,b=y。
观察方程左右,令x和z等于1和0,即可得出这个[ ]为=
一个补充的知识点:
则方程组可写为Ax=b。
矩阵乘法的一些性质:
0A=0,A0=0
IA=A,AI=A
A(BC)=(AB)C
A(B+C)=AB+AC
(B+C)A=BA+CA
7.逆矩阵:
定义:设A是n阶方程,如果存在n阶方阵B使得AB=BA=I,则称A是可逆的(或者非奇异的),B是A的一个逆矩阵,否则称A是不可逆的(或奇异的)。
定理:逆矩阵如果存在,则逆矩阵唯一。
定义:det运算符:
定理:设A、B是n阶方程,则:det(AB)=det(A)det(B)
证明的提示:构造![]()
引理:det(A1A2…As)=det(A1)(A2)…(As)。
引理:设A为n阶方阵,AX=0有非零解的充分必要条件是A奇异。
引理:设A为n阶方阵,若∃B为n阶方阵,使得AB=I(或BA=I),则A可逆且A-1=B。
引理:若det(A)≠0,则det(A-1)=(det(A))-1。
求解逆矩阵的方法:
①待定系数法
②公式法:A-1=(1/(det(A)))A*
③定义法:若AB=I,则B=A-1
逆矩阵的性质:
(A-1)-1=A
(AB)-1=B-1A-1
(kA)-1=k-1A-1
定理:设A为n阶方阵,若A可逆,则线性方程组AX=b有唯一解X=A-1b
8.初等变换:
定义:矩阵的初等行/列变换
<1>用一个非零的数乘以某行
<2>将某一行的k倍加到另一行
<3>互换两行
定义:单位阵I经过一次初等变换得到的矩阵称为初等矩阵。
初等矩阵:
定理:用初等矩阵左(右)乘矩阵A,相当于对矩阵A实行相应的初等行(列)变换
定理:初等矩阵都可逆。
定义:若矩阵B可以由矩阵A经过一系列初等变换得到,则称A与B相抵(等价),记做A≌B。
定理:相抵是一种等价关系。
初等变换求逆矩阵:构造一个n×2n的矩阵(AI)
A-1(AI)=(A-1AA-1)=(IA-1)
(AI)→…→(IA-1)一系列的初等变换
最近发现一些网站盗用我的blog,这实在不能忍(™把关于我的名字什么的全部删去只保留文本啥意思。。)!!希望各位转载引用时请注明出处,谢谢配合噢~



