2017清北学堂(提高组精英班)集训笔记——动态规划Part1
诶~时间过得真是快,马上到了第三天的动态规划了,这是我认为我最难理解的部分,嗯。。老师特别好——杨乐,讲课速度能接受(声音真的好听啊。。滑稽脸)。
经典例题:数字金字塔(Luogu 1216)
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
我们现在这里讨论搜索如何实现:
状态:目前在第x行第y列
行动:向左走,向右走
例如:一个底边为4的三角形共有八种状态:
![]()
我们按照一般的搜索思路,进行深度优先搜索:
1 void dfs(int x,int y,int val) 2 { 3 val+=a[x][y];//加上权值 4 if(x==n-1) 5 { 6 if(val>ans) ans=val;//更新更大的ans 7 return; 8 } 9 dfs(x+1,y,val);//往左边走 10 dfs(x+1,y+1,val);//往右边走 11 }
考虑时空效率,DFS确实很暴力啊,有没有什么优化呢??
我们引入“冗余搜索”这个概念:无用的,不会改变答案的搜索
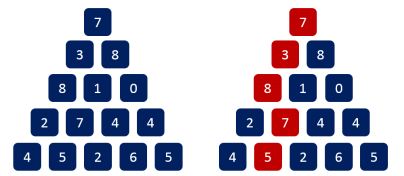
例子:观察下面两个例子。用两种方式都能到达第 3 行第 2 列,只是路径不同,同时走到这个点两条路权值和不一样,其中一个总和为 8,一个总和 12。
那么可以观察可得,总和为 8 的搜索是冗余的(不会改变答案),即使不继续搜索, 答案也不会改变。
因为 12 往下搜索,无论往左往右,都会比 8 对应的路径大。
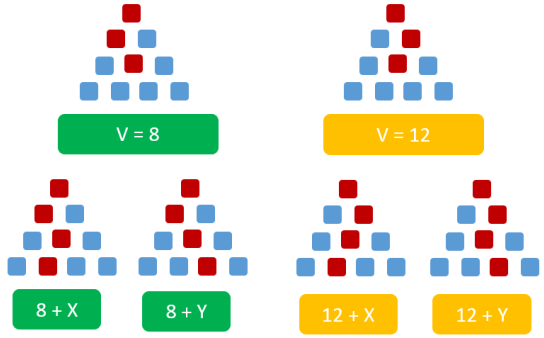
可见,冗余就是剪枝的“枝”,那么如何利用冗余搜索,来优化程序呢?
我们可以对于每一个位置记录一个值 F,代表搜索到此位置时,最大的路径和是多
少 ,这样如果搜到某一个位置时候,路径和不大于记录值F,说明这个搜索是冗余搜索,直接退出,如果大于,就需要更新F值并且继续搜索。
我们就把这种搜索叫做记忆化搜索,根据之前的“记忆”来优化搜索;在这道题中,每个位置的“记忆”就是最大的路径和
1 //T1:数字金字塔(记忆化搜索) 2 void dfs(int x,int y,int val) 3 { 4 val+=a[x][y]; 5 // 记忆化过程 6 if(val<=f[x][y]) return;//发现冗余搜索,退出 7 f[x][y]=val;//f[x][y]记录这个点当前最大权值 8 if(x==n-1)//如果搜到了最后一个点,ans更新保存最大值,退出即可 9 { 10 if(val>ans) ans=val; 11 return; 12 } 13 dfs(x+1,y,val);//继续搜索 14 dfs(x+1,y+1,val); 15 }
经典例题:采药(Luogu 1048)
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
草药 1 :时间 71;价值 100
草药 2 :时间 69;价值 1
草药 3 :时间 1 ;价值 2
@最优选择:草药 2+3:总时间 70;总价值 3
这题是经典的背包问题,和金字塔问题不同的地方在于:它是有重量限制的。
我们还是先用记忆化搜索来思考这个问题:
状态:目前已经决定到第x件物品,当前背包中物品总重量为w,总价值为v;
行动:这件物品取还是不取;
约束:物品总重量不超过w(背包总重量);
目标:物品总价值最大;
比较下列两种情况:
状态相同:x1=x2(当前搜索到同一件物品),w1=w2(当前总重量相等);
价值不同:但它们的背包总价值不同,其中v1<v2。(经过不同的路径到达同一个点,但是后者的val更大)
则我们可以说状态1为冗余的,因为它肯定比状态2要差。
*记忆化:对于每个状态(x,w),记录对应的v的最大值。
1 //T5:采药(记忆化搜索) 2 void dfs(int t,int x,int val)//t为剩余时间,x为当前决定的第几株草药,val为总价值 3 { 4 //记忆化 5 if(val<=f[t][x]) return; 6 f[t][x]=val; 7 if(x==n)//把草药采摘完了,直接返回 8 { 9 if(val>ans) ans=val;//更新最大值ans 10 return; 11 } 12 dfs(t,x+1,val); 13 if(w[x]<=t) dfs(t-w[x],x+1,val+v[x]);//如果我们还有时间,继续采摘! 14 }
那好的,说完记忆化搜索我们回到正题:动态规划啦!记忆化搜索是DP的基础。
我们再回到数字金字塔这个问题来,下图的黑色三角形是我们记忆化搜索的路径,我们想想,是不是可以不通过记忆化搜索就能得到这个黑色三角形??

最优性:设走到某一个位置的时候,它达到了路径最大值,那么在这之前,它走的每一步都是最大值。
-考虑这条最优的路径:每一步均达到了最大值
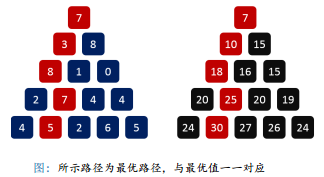
最优性的好处:要达到一个位置的最优值,它的前一步也一定是最优的。
-考虑图中位置,如果它要到达最优值,有两个选择,从左上方或者右上方的最优值得到:
所以从这里,定义动态规划(DP):只记录状态的最优值,并用最优值来推导出其他的最优值。
记录 F[i][j] 为第 i 行第 j 列的路径最大值,有两种方法可以推导:(两个分支两种状态,选取最大)
@顺推:用 F[i][j] 来计算 F[i+1][j],F[i+1][j+1]
@逆推:用 F[i-1][j],F[i-1][j-1] 来计算 F[i][j]
这两种思考方法也是动态规划中最基本的两种方法,解决绝大部分DP我们都可以采用这样的方法。

1 //T2:数字金字塔-顺推(有点类似于记忆化搜索的思路) 2 f[0][0]=a[0][0]; 3 for(int i=0;i<n-1;++i) 4 for(int j=0;j<=i;++j)//f数组为最优值路径(黑色金字塔,a为源数据数组(紫色金字塔) 5 { 6 //分别用最优值来更新左下方和右下方 7 f[i+1][j]=max(f[i+1][j],f[i][j]+a[i+1][j]);//和当前的f[i+1][j]比较 8 f[i+1][j+1]=max(f[i+1][j+1],f[i][j]+a[i+1][j+1]);//和当前的f[i+1][j+1]比较 9 }
1 //T4:数字金字塔-逆推(自顶向下) 2 f[0][0]=a[0][0]; 3 for(int i=0;i<n;++i)//单独处理 4 { 5 f[i][0]=f[i-1][0]+a[i][0];//最左的位置没有左上方 6 f[i][i]=f[i-1][i-1]+a[i][i];//最右的位置没有右上方 7 for(int j=1;j<i;++j)//在左上方和右上方取较大的 8 f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]; 9 } 10 //答案可能是最后一行的任意一列 11 ans=0; 12 for(int i=0;i<n;++i) 13 ans=max(ans,f[n-1][i]);
*转移方程:最优值之间的推导公式。
@顺推:
F[i+1][j] = MAX (F[i][j] + a[i+1][j]);
F[i+1][j+1] = MAX (F[i][j] + a[i+1][j+1]);
@ 逆推:
F[i][j] = MAX (F[i-1][j], F[i-1][j-1]) + a[i][j]; (注意!逆推时要注意边界情况! )
顺推和逆推本质上是一样的(复杂度一致);顺推和搜索的顺序类似;而逆推则是将顺序反过来;顺推考虑的是“我这个状态的下一步去哪里” ,逆推的考虑的是“从什么状态可以到达我这里” 。 同时在转移的过程中我们要时刻注意边界情况。
我们还可以改变搜索顺序:
1 //T3:数字金字塔-逆推/路径自底向上 2 //改变顺序:记录从底部向上走的路径最优值 3 for(int i=0;i<n;++i) 4 f[n-1][i]=a[n-1][i];//备份底部自己这一行 5 //逆推过程:可以从左下方或右下方走过来;没有边界情况 6 for(int i=n-2;i>=0;--i) 7 for(int j=0;j<=i;++j) 8 f[i][j]=max(f[i+1][j+1],f[i+1][j])+a[i][j];//当前[i][j]左下方和右下方取较大加上当前的 9 //答案则是顶端 10 ans=f[0][0]; 11 //和之前的逆推区别:这样较自顶向下不需要判断边界,更加简单
*转移顺序:最优值之间的推导顺序
一个小问题:在数字金字塔中,为什么能够使用动态规划 呢??答:因为有明确的顺序: 自上而下 ,也就是说,能划分成不同的阶段,这个阶段是逐步进行的,这和搜索顺序也是类似的,所以,只要划分好阶段, 从前往后推,与从后往前推都是可以的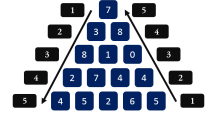
接下来我们进入重点,还是回到刚才的采药问题,我们回忆刚才这题的记忆化搜索。
状态设计:记录 F[i][j] 为, 已经决定前 i 件物品的情况,在总重量为 j 的情况下,物品总价值的最大值。同样也是有两种方法可以推导:
@ 顺推: “我这个状态的下一步去哪里”
@ 逆推: “从什么状态可以到达我这里”
当前状态: F[i][j] 为, 已经决定前 i 件物品的情况,在总重量为 j的情况下,物品总价值的最大值。
@顺推: “我这个状态的下一步去哪里” :我现在要决定下一件物品取还是不取。
> 如果不取的话,可以达到状态 F[i+1][j];
> 如果取的话,可以达到状态 F[i+1][j+w[i+1]](需要满足重量约束);
@ 逆推: “从什么状态可以到达我这里” :考虑我这件物品取不取。
> 如果是不取的,那可以从 F[i-1][j] 推导而来;
> 如果是取的,可以从 F[i-1][j-w[i]] 推导而来的(同样需要满足重量约束)
1 //T6:采药(DP/顺推) 2 for(int i=0;i<n;++i) 3 for(int j=0;j<=t;++j) 4 { 5 //不取 6 f[i+1][j]=max(f[i+1][j],f[i][j]); 7 //取 8 if(j+w[i]<=t)//满足重量限制(类比背包问题) 9 f[i+1][j+w[i]]=max(f[i+1][j+w[i]],f[i][j]+v[i]); 10 } 11 //答案 12 ans=0; 13 for(int i=0;i<=t;++i) ans=max(ans,f[n][i]);
1 //T7:采药(DP/逆推) 2 for(int i=1;i<=n;++i) 3 for(int j=0;j<=t;++j) 4 { 5 //不取 6 f[i][j]=f[i-1][j]; 7 //取 8 if(j>=w[i])f[i][j]=max(f[i][j],f[i-1][j-w[i]]+v[i]);//如果还有时间可以采摘 9 } 10 //答案 11 ans=0; 12 for(int i=0;i<=t;++i) ans=max(ans,f[n][i]);
学到这里,我们大概摸清了动态规划的轮廓是什么,使用动态规划较DFS解决了时间上的问题,那么我们可不可考虑解决一下空间上的问题呢?由于动态规划满足”无后效性原则“,当前状态F[i]之和上一个状态F[i-1]有关,和上个状态之前的都没有关系,所以我们可以考虑使用滚动数组来保存这两个状态,一上一下,互为前后状态,节省空间啊!!
这就是——数组压缩!
所以一个直观的做法是,记录两个数组,分别记录 F[i-1] 与 F[i] 的值。
*但更进一步,我们可以甚至不记录两行,只记录一行的状态。
-我们倒着枚举,在 F[i-1] 数组中逐步更新,让它逐步变为 F[i]。

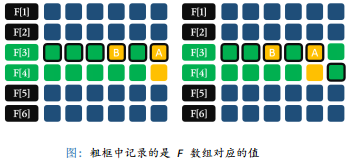
因为是倒着枚举的,先枚举的位置都已经无用了,可以直接用 F[i] 的元素来替换。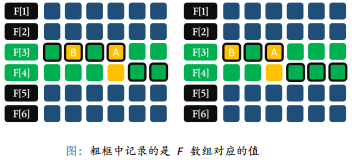
1 //T10:采药(DP/逆推/数组压缩) 2 //用一个一维数组来代替二维数组 3 for(int i=1;i<=n;++i) 4 for(int j=t;j>=0;--j)//重量:倒着枚举 5 { 6 //不取:对数组没有影响 7 //f[i][j]=f[i-1][j]; 8 //取 9 //if(j>=w[i])f[i][j]=max(f[i][j],f[i-1][j-w[i]]+v[i]); 10 if(j>=w[i])f[j]=max(f[j],f[j-w[i]]+v[i]);//如果还有采药时间,执行 11 } 12 //在枚举过程中,大于j的位置等于f[i][j],小于j的位置等于f[i-1][j]
上题的采药,就是一类经典的背包问题——01背包,下面我们来说说第二类经典的背包问题——完全背包问题:
经典例题:Piggy-Bank(POJ 1384)
现在有 n 种硬币, 每种硬币有特定的重量 cost[i] 和它对应的价值val[i]. 每种硬币可以无限使用。已知现在一个储蓄罐中所有硬币的总重量正好为 m 克, 问你这个储蓄罐中最少有多少价值的硬币? 如果不可能存在 m 克的情况, 那么就输出“This is impossible.”
我们也把这类问题归入到背包问题当中: 有物品,重量限制,价值最大。
* 但与采药问题不同的是,每件物品可以无限使用。
推导状态转移方程:
当前状态: F[i][j] 为, 已经决定前 i 件物品的情况,在总重量为 j的情况下,物品总价值的最小值。
@ 顺推: “我这个状态的下一步去哪里” :考虑我这件物品取多少件。
> 如果是不取的,那可以推导到 F[i+1][j];
> 如果是取一件,那可以推导到 F[i+1][j+w[i]];
> 如果是取 k 件,那可以推导到 F[i+1][j+w[i]*k]
1 //T8:Piggy-Bank(DP/顺推) 2 //初值处理:由于问题求的是最小值,所以先把所有状态赋值为最大值 3 for(int i=1;i<=n+1;++i) 4 for(int j=0;j<=m;++j) f[i][j]=INF; 5 //第一件还没取,重量为0 6 f[1][0]=0; 7 for(int i=1;i<=n;++i)//i:已经决定的物品 8 for(int j=0;j<=m;++j)//j:总重量 9 for(int k=0;j+w[i]*k<=m;++k)//k:这件物品取多少件 10 f[i+1][j+w[i]*k]=min(f[i+1][j+w[i]*k],f[i][j]+p[i]*k); 11 //w重量;p[]价值
当前状态: F[i][j] 为, 已经决定前 i 件物品的情况,在总重量为 j
的情况下,物品总价值的最大值。
@ 逆推: “从什么状态可以到达我这里” :考虑我这件物品取多少件。
> 如果是不取的,那可以从 F[i-1][j] 处推导得到;
> 如果是取一件,那可以从 F[i-1][j-w[i]] 处推导得到;
> 如果是取 k 件,那可以从 F[i-1][j-w[i]*k] 处推导得到;
1 //T9/work1:Piggy-Bank(DP/逆推) 2 for(int i=0;i<=n;++i) 3 for(int j=0;j<=m;++j) g[i][j]=INF; 4 g[0][0]=0; 5 for(int i=1;i<=n;++i) 6 for(int j=0;j<=m;++j) 7 for(int k=0;j>=w[i]*k;++k) 8 g[i][j]=min(g[i][j],g[i-1][j-w[i]*k]+p[i]*k);//三重循环开销太大啦!!我需要一个优化QAQ
 ,我们对逆推进行优化:
,我们对逆推进行优化:
逆推:观察和逆推相关的状态。
假设 w[i]=3,则 F[i][6] 与 F[i-1][0,3,6] 相关; F[i][7] 与F[i-1][1,4,7] 相关;与此同时, F[i][3] 与 F[i-1][0,3] 相关;F[i][4] 与 F[i-1][1,4] 相关。
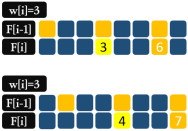
则可以得到, 实际上与 F[i][j] 相关的状态只比 F[i][j-w[i]] 多一个。
则所以我们可以这样推导:
> 如果是不取的,那可以从 F[i-1][j] 处推导得到;
> 如果是取一件或更多,那可以从 F[i][j-w[i]] 处推导得到; (因为是可以取任意件,所以从 F[i] 中取最优而不是从 F[i-1] 中取) 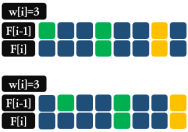
而从这种逆推也可以方便的写出数组压缩。
1 //T9/work2:Piggy-Bank(DP/逆推优化) 2 for(int i=0;i<=n;++i) 3 for(int j=0;j<=m;++j) g[i][j]=INF; 4 g[0][0]=0; 5 for(int i=1;i<=n;++i) 6 for(int j=0;j<=m;++j) 7 { 8 g[i][j]=g[i-1][j];//不取 9 if(j>=w[i])g[i][j]=min(g[i][j],g[i][j-w[i]]+p[i]); 10 }
1 //T9/work3:Piggy-Bank(DP/逆推优化/数组压缩) 2 for(int j=0;j<=m;++j)f[j]=INF; 3 f[0]=0; 4 for(int i=1;i<=n;++i) 5 for(int j=0;j<=m;++j)//顺着枚举——完全背包(逆着枚举——01背包) 6 if(j>=w[i])f[j]=min(f[j],f[j-w[i]]+p[i]);
同样地,我们还可以用位运算对一维进行优化,嗯。。由于我比较懒,我就直接引了P2O5大佬的代码:https://zybuluo.com/P2Oileen/note/816892#动态规划
1 //原来写01背包的时候,循环是这么写的: 2 for(int i=1;i<=n;i++) 3 { 4 for(j=m;j>=a[i];j--) if(f[j-a[i]]) f[j]=1;//这个物品被取用了,标记为1 5 } 6 //可以改成位运算版本的,减少一重循环更快~ 7 for(int i=1;i<=n;i++) 8 { 9 f=f|f<<a[i];//f或f左移a[i]位(×2^a[i]) 10 }
背包计数问题:
经典例题:集合(Luogu 1466)
对于从 1 到 N (1 <= N <= 39) 的连续整数集合,能划分成两个子集合,且保证每个集合的数字和是相等的。举个例子,如果 N=3,对于[1, 2, 3] 能划分成两个子集合,每个子集合的所有数字和是相等的:- [3] 和 [1,2]
这是唯一一种分法(交换集合位置被认为是同一种划分方案,因此不会增加划分方案总数)如果 N=7,有四种方法能划分集合 [1, 2, 3, 4, 5,6, 7],每一种分法的子集合各数字和是相等的:
- [1,6,7] 和 [2,3,4,5] (注: 1+6+7=2+3+4+5)
- [2,5,7] 和 [1,3,4,6]
- [3,4,7] 和 [1,2,5,6]
- [1,2,4,7] 和 [3,5,6]
给出 N,你的程序应该输出划分方案总数,如果不存在这样的划分方案,则输出 0。程序不能预存结果直接输出(不能打表)。
这里引入背包模型:
* 物品:可以把所有的数字看作物品。对于数字 i,其对应的重量为 i,则我们需要求出装满载重为 M 的背包的方案数(其中 M 为所有数总和的一半)。
* 状态:(仿照之前的方法)设 F[i][j] 为已经考虑完数字 1-i 了,当前数字总和为 j 的总方案数。
* 状态转移方程 - 顺推:考虑有没有取数字 i。
没取: F[i+1][j] += F[i][j]
取了: F[i+1][j+i] += F[i][j] (j+i<=M)
* 状态转移方程 - 逆推:考虑有没有取数字 i。
F[i][j] = F[i-1][j] + F[i-1][j-i] (j>=i)
1 //T14/work1:集合(DP/顺推) 2 //初值:(什么都不取)和=0,有一种方案 3 f[1][0]=1; 4 for(int i=1;i<=n;++i) 5 for(int j=0;j<=m;++j) 6 { 7 f[i+1][j]+=f[i][j]; 8 if(i+j<=m)f[i+1][i+j]+=f[i][j]; 9 }
1 //T14/work2:集合(DP/逆推) 2 f[0][0]=1; 3 for(int i=1;i<=n;++i) 4 for(int j=0;j<=m;++j) 5 { 6 f[i][j]=f[i-1][j]; 7 if(j>=i)f[i][j]+=f[i-1][j-i]; 8 }
1 //T14/work3:集合(DP/逆推/数组压缩) 2 g[0]=1; 3 for(int i=1;i<=n;++i) 4 for(int j=m;j>=i;--j)//注意要倒着枚举 5 g[j]+=g[j-i];
完全背包计数问题:
经典例题:货币系统(Luogu 1474)
母牛们不但创建了它们自己的政府而且选择了建立了自己的货币系统。由于它们特殊的思考方式,它们对货币的数值感到好奇。
传统地,一个货币系统是由 1,5,10,20 或 25,50, 和 100 的单位面值组成的。
母牛想知道有多少种不同的方法来用货币系统中的货币来构造一个确定的数值。
举例来说, 使用一个货币系统 [1,2,5,10,...] 产生 18 单位面值的一些可能的方法是:18x1, 9x2, 8x2+2x1, 3x5+2+1, 等等其它。写一个程序来计算有多少种方法用给定的货币系统来构造一定数量的面值。
* 物品:可以把所有的货币看作物品。对于每种货币,其对应的重量为它的面值(注意到与前一道题目相比,每个物品是可以取任意件的)。
* 状态:(仿照之前的方法)设 F[i][j] 为已经考虑完前 i 种货币了,当前钱的总和为 j 的总方案数。
* 状态转移方程 - 逆推:考虑货币 i 取了多少件。
F[i][j] = ∑ F[i-1][j - w[i]*k] (加法原理噢~)
1 //T15/work1:货币系统(DP/逆推) 2 f[0][0]=1; 3 for(int i=1;i<=v;++i) 4 for(int j=0;j<=n;++j) 5 for(int k=0;k<=j/a[i];++k) 6 f[i][j]+=f[i-1][j-a[i]*k];
1 //T15/work2:货币系统(DP/逆推/数组压缩) 2 g[0]=1; 3 for(int i=1;i<=v;++i) 4 for(int j=a[i];j<=n;++j) 5 g[j]+=g[j-a[i]];
总之,我们在使用动态规划解决问题的时候,要时刻注意一下:
1.划分清楚状态,状态转移方程明了清晰
2.注意顺序
3.尽量使用数据压缩,剪枝之类,比如列出边界条件,位运算优化,多维变滚动甚至一维等。

最近发现一些网站盗用我的blog,这实在不能忍(™把关于我的名字什么的全部删去只保留文本啥意思。。)!!希望各位转载引用时请注明出处,谢谢配合噢~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号