Hanoi汉诺塔问题——递归与函数自调用算法

题目描述 Description

有N个圆盘，依半径大小（半径都不同），自下而上套在A柱上，每次只允许移动最上面一个盘子到另外的柱子上去（除A柱外，还有B柱和C柱，开始时这两个柱子上无盘子），但绝不允许发生柱子上出现大盘子在上，小盘子在下的情况，现要求设计将A柱子上N个盘子搬移到C柱去的方法。 

输入输出格式 Input/output

输入格式：
一行,n<=20
输出格式：

步数及各种圆盘要移动的步骤

输入输出样例 Sample input/output

样例测试点#1

输入样例：

2

输出样例：

1：From A to B

2：From A to C

3：From B to C

样例测试点#2

输入样例：

3

输出样例：

1：From A to C

2：From A to B

3：From C to B

4：From A to C

5：From B to A

6：From B to C

7：From A to C

思路：

本题是典型的递归程序设计题。

    (1)当N=1 时，只有一个盘子，只需要移动一次:A—>C;

    (2)当N=2时，则需要移动三次：

        A------ 1 ------> B, A ------ 2 ------> C, B ------ 1------> C. 

    (3)如果N=3，则具体移动步骤为：

 

 

    

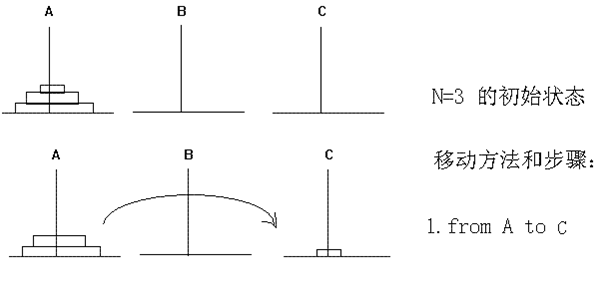
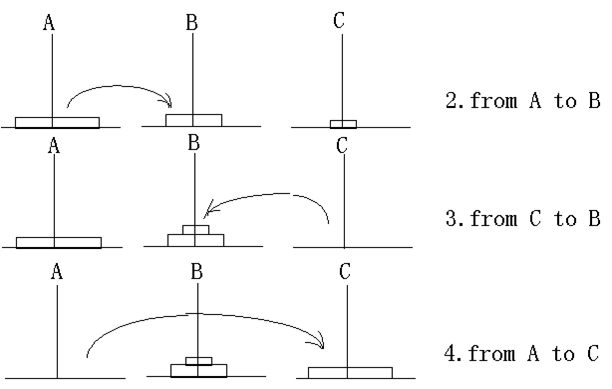
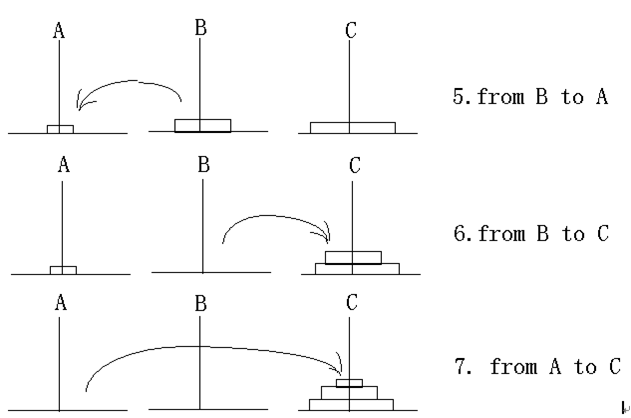
假设把第3步，第4步，第7步抽出来就相当于N=2的情况（把上面2片捆在一起，视为一片）：

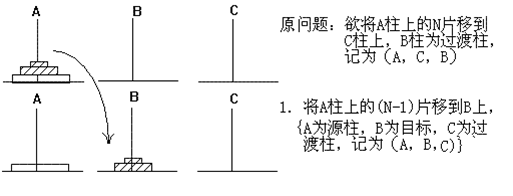
所以可按“N=2”的移动步骤设计：

       ①如果N=0，则退出，即结束程序;否则继续往下执行;

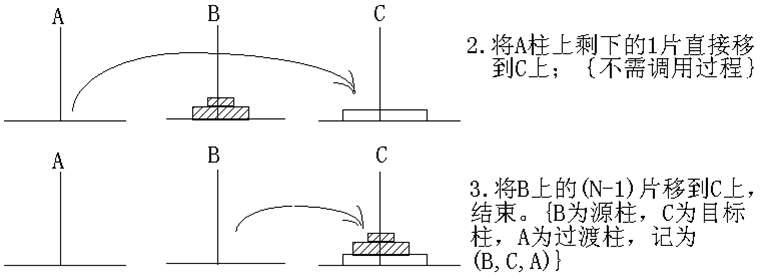
       ②用C柱作为协助过渡，将A柱上的（N-1）片移到B柱上，调用过程mov(n-1, a,b,c);

       ③将A柱上剩下的一片直接移到C柱上;

       ④用A柱作为协助过渡，将B柱上的（N-1）移到C柱上，调用过程mov (n-1,b,c,a)

代码如下：

#include <stdio.h>
int k=0;//统计步数 
void Hanoi(int n,char a,char b,char c)
{    
    if(n==0)//0的话,没什么好玩的了,直接退出！！ 
    {
        return ;        
    }  
    else
    {        
        Hanoi(n-1,a,c,b);
        k++;
        printf("%d：From %c to %c\n",k,a,c);
        Hanoi(n-1,b,a,c);
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    Hanoi(n,'A','B','C');    
    return 0;
}