微积分与概率统计---生命动力学的建模

这本书<<微积分与概率统计>>

------ 生命动力学的建模

偶尔更新这个笔记.

 

1,伽马分布

g(x) = (x^n)  * [e^(-x)]

n=0 , n=1 ....如图为:

 

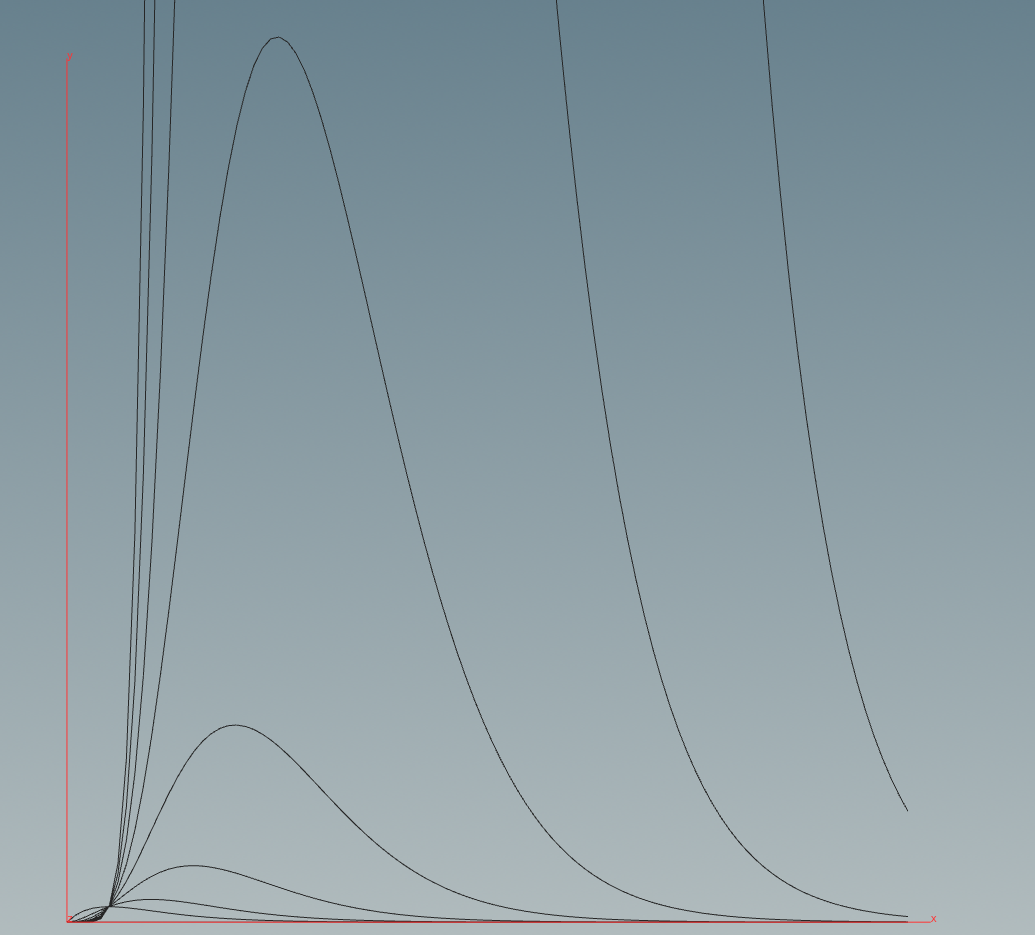
通过对n=0 n=1 ... 分别求一阶导，二阶导，确定其图像

2, 指数函数y = a^x

在<<托马斯微积分>>求这个导数是最简单的方法，目前能想到3中方法:

<1>第一种方法最简单:

两边同时ln , 即 lny = ln a^x   即: lny = xlna

两边同时开导:  1/y * y'  =  lna     

移项: y' = lna * y = lna * (a^x)

<2>第二种方法:

因为 a = e^ (lna)

所以a^x = e^(xlna)

给 y = e^(xlna) 开导用链式法则:

y' = e^(xlna) * xlna  替换e^(xlna) 为a^x

即y'= lna * (a^x)

<3>第三种方法从导数的定义出发。

目前智能表示到这(图书2.8章,214页)

 

 

 

正态分布:

f(x) = e^ [ (-1/2) * (x^2)],y最大为1.关于y对称的图像

 

。。。