微分学习

1,曲线y = sqrt(x) 和 点(3/2,0) 最近距离为多少

 

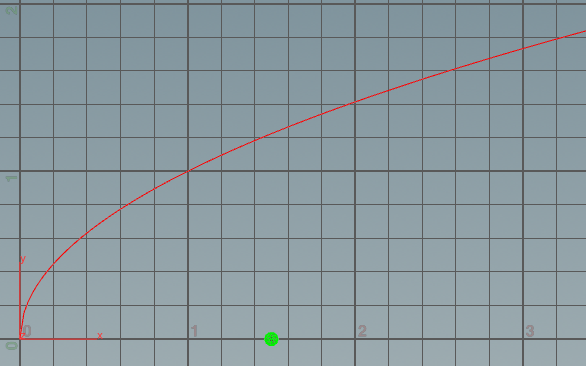
设最近点为(x,y)

则D = d^2 = (x-3/2)^2  + (y-0)^2 

所以D = (x-3/2)^2  + [sqrt(x)-0]^2  因为y = sqrt(x)

所以D = (x-3/2)^2 + x = x^2 - 2x + 9/4

D' = 2x-2  D' = 0 时: x = 1

D'' = 2   图像为凹向上,则D有最小值。 所以x= 1，距离必须是最小值

x-1 带入 D= d^2  = 5/4  , 所以d = sqrt(5)/2

 

2,求线性化

 f(x) = cos(x) 在PI/2 的线性化:

L = f(a) + f'(x)(x-a)

f(PI/2) = 0

f'(x) = -sin(x)

f'(PI/2) = -1

L = 0 + -1(x-PI/2) = -x + PI/2

 

3,隐函数微分法:

求dy/dx y^2 = x;

两边求dy/dx , 把y = f(x) 当做x的可微函数处理

2y * dy/dx  = 1

dy/dx = 1/2y

 

4,微分形势下的导数

xy^2 - 4x^3/2 - y = 0 

求dy

求xy^2比较麻烦 ,要用乘法法则

d(x) * y^2  + d(y^2)x = y^2dx + 2xydy

所以原始的dy = y^2dx + 2xydy  - 6x^(1/2) dx - dy =0 

所以: dy/dx = [6x^(1/2) - y^2] / (2xy - 1)

 

 

微分利器：预估变化的量

 

 

 

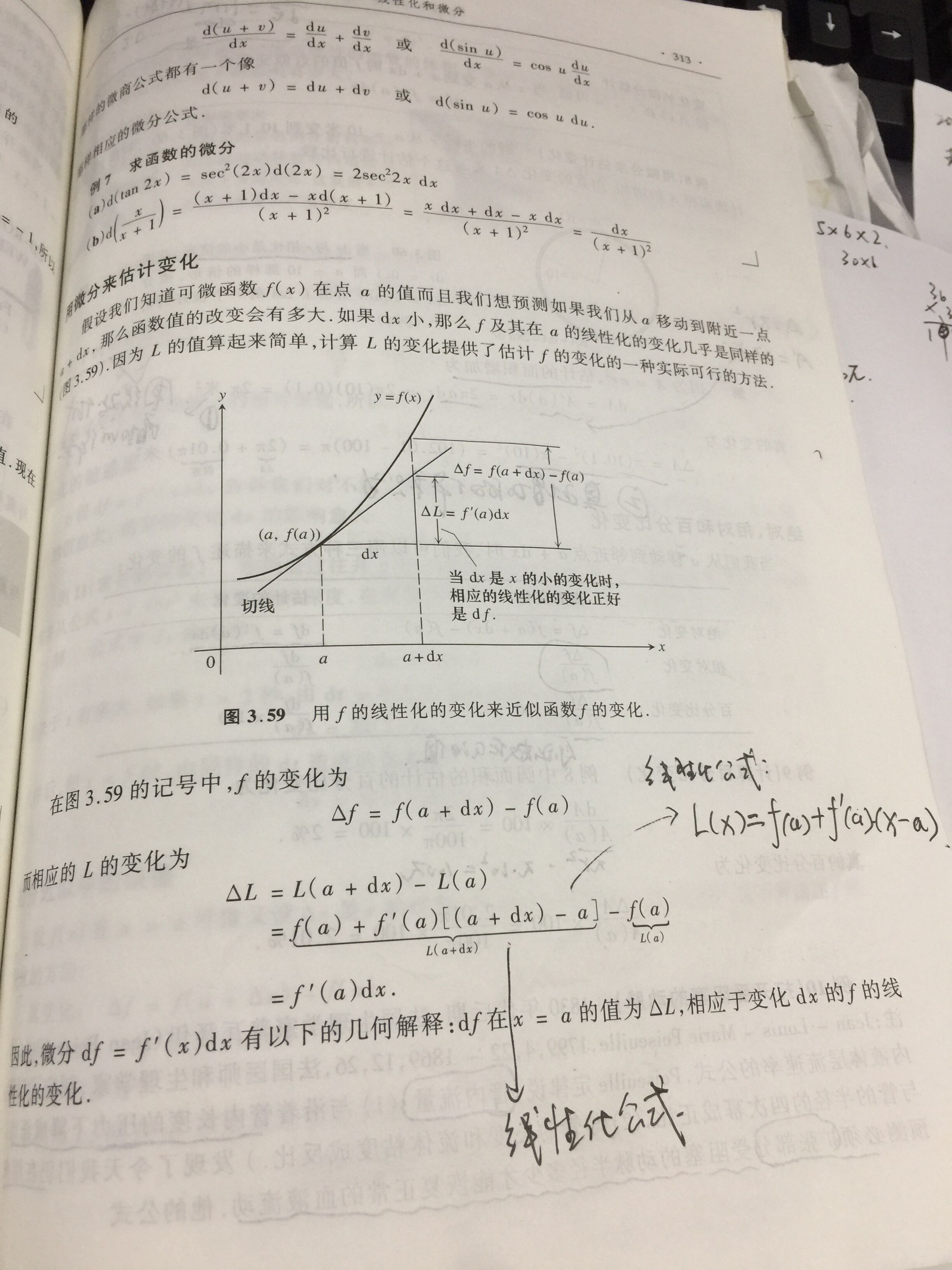
5,微分估计变化

圆的半径r从a=10 增加到10.1(dr = 0.1),用dA 来估计面积A的增加。并且真正增加了多少。

微分法估计圆面积增加:

dA = (π * r^2) ' = 2 * π * r * dr =  2 * PI * 10 * 0.1 = 2 π

真正的面积增加:

ΔA = π(10.1)^2 + π(10)^2 = 2π + 0.01π  [其中0.01π就是微分估计得误差]

 

6,微分变化求圆柱薄壳体积:

如图所示:中间红色半径为6,薄壳厚度为0.5,高度h = 30

求薄壳体积:

圆柱体积公式为A = π * r^2 * h

那么预估增加的体积公式为:dA = 2 π r * h * dr  = 2 * π * 6 * 30 * 0.5 = 180 π

 

Newton-Raphson method(牛顿-拉佛森):  比如求x^5 = 10, 求x.

动机是例如x^2 - 2 = 0 = f(x) ,求x,我们可以手算,√2 = 2.0 ，利用python计算 : math.sqrt(2) = 1.41421 。 这是一个方法。

如何用Newton method做。牛顿法就是把函数曲线的某点线性化公式。直接上附图:

 

 

用Python求一个x^2 - 2.0 = 0 

把初始值x0 = 0.01, 让他迭代100次，也能计算出来

书中把初始值x0 = 1, 值迭代4次，就能迭代出来。

如果是计算机，我首选把初始值设为0.01,或者更小的，让他迭代去。 谁特么知道初始值设置多少合适

关键更牛逼的知道x^2 = 2.0 时候 x肯定有正负值这一说。

如果将代码的初始x0从负值开始 ，一样会求出负根speculate_base_x0(-0.1,100) ，结果是-1.41421360012

import math

#f(x)  = x^2 - 2.0 = 0
#f'(x) = 2x
#Newton:

def speculate_base_x0(x0,numIter):
    begin_value = x0
    for n in range(0,numIter,1):
        begin_value = begin_value - (math.pow(begin_value,2)-2) / (2*begin_value)

        # check if f(x) == 0 , so it's the right Answer
        if math.pow(begin_value,2) - 2.0 <= 0.000001:
            return begin_value
    return None


if __name__ == "__main__":
    print speculate_base_x0(0.01,100)

 

 

Houdini newton-method fracture:

python code:

node = hou.pwd()
geo = node.geometry()

# Add code to modify contents of geo.
# Use drop down menu to select examples.

# f(x) = z^6 - 1 = 0
# f'(x) = 6z^5
import math
def Newton(z):
    for x in range(20):
        fx = z*z*z*z*z*z - 1
        dx = 6 * z*z*z*z*z
        next = z - fx / dx
        if abs(z*z*z*z*z) > 10e10:
            return None
        if abs((next*next*next*next*next*next) -1 ) < 0.00001:
            return z
        z = next
    return None
    
# getbounding box
bbox = geo.boundingBox()
bbox_min = bbox.minvec()
bbox_max = bbox.maxvec()


getPoints = geo.points()

for pt in getPoints:
    pos = pt.position()
    x = hou.hmath.fit(pos.x(),bbox_min.x(),bbox_max.x(),-1.0,1.0)
    y = hou.hmath.fit(pos.y(),bbox_min.y(),bbox_max.y(),-1.0,1.0)
    z = complex(x , y)
    root = Newton(z)
    if root:
        pt.setAttribValue("Cd",hou.Vector3( 1,0,0))
        
        

 

 

识别图形:

<1>:

Y 代表s 位移

X 代表t 时间

(a) ,什么时候速度等于0

因为速度是ds/dt ,则当速度为0时候，函数图像取到极值. t= 0,6,12 这3个点 ，速度都位0

(b),什么时候加速度等于0

加速度为0，则速度最大，也是函数的拐点。3,9 为函数的拐点 ，是a = d''s/dt'' = dv/dt = 0的点

(c)向后运动，则速度为负数。 如图所知 t 在[0 , 6] ,t>14的时候

(d)向前运动,t在[6,12] 

 

<2>

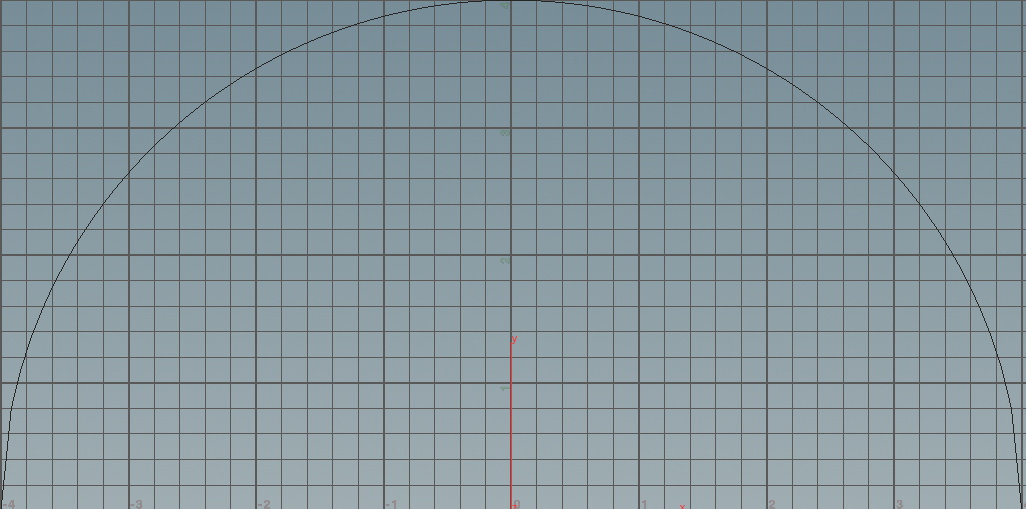
@P.y = sqrt(16 - @P.x * @P.x);

a:在0点时候

 

 

 导数应用总结：

1,绝对最大值，绝对最小值(absolute extrema)

2,局部最大值，局部最小值

3,罗尔定理(Rolle),如果在函数y = f(x) 在[a,b]中的每一点连续，又假设在每一点可微,如果f(a) = a(b) = 0,那么在(a,b)中至少有一个数c,f'(c) = 0 

4,中值定理(斜线上的Rolle定理)

    [f(b)-f(a)] / (b-a) = f'(c)

    解释:在闭区间[a,b],y=f(x) 连续并且处处可微,那么至少有一点c 满足上式

    物理解释:a,b区间的平均变化率是[f(b) - f(a)] / (b-a), 而f'(c) 是f 在 x= c的瞬时变化率,中值定理说明在某个内点处的瞬时变化率一定等于整个区间的平均变化率。

5,递增和凹性

   (1) 一阶导数检验法

   (2)凹性

   (3)拐点

   (4)二阶导数检验法

         如果f'(c) = 0 且f''(c) < 0,f在x = c 取得局部最大值

         如果f'(c) = 0 且f''(c) > 0,f在x = c 取得局部最小值

6,自治微分方程的图形解

    <1> y^2 = x + 1

    求dy/dx

    求导数形式:dy/dx = 1/2y

    微分形式:  2ydy = dx  =>  dy = dx/2y

   <2>平衡点或静止点

    dy/dx =0 的y的值称作静止点或者平衡点

   比如自治微分方程:dy/dx = (y+1)(y-2) ，平衡点是y=-1 和 y=2

7,其他的方面：

    回归

    建模和最优化