NOTE_PYTHON机器学习及实践-从零开始通往KAGGLE竞赛之路
NOTE_PYTHON机器学习及实践-从零开始通往KAGGLE竞赛之路
作为笔记记录阅读,因为调用库的更新,相对应的对代码也进行了更新。
1.机器学习综述
- 所谓具备“学习”能力的程序都是指它能够不断地从经历和数据中吸取经验教训,从而应对未来的预测任务。我们习惯地把这种对未知的预测能力叫做泛化力(Generalization)。
- 机器学习具备不断改善自身应对具体任务的能力->性能(Performance)。
任务种类:
- 监督学习(Supervised Learning)
- 关注事物对未知表现的预测
- 分类问题(Classification)和回归问题(Regression)
- 无监督学习(Unsupervised Learning)
- 倾向于对事物本身特性的分析
- 数据降维(Dimensionality Reduction)和聚类问题(Clustering)
一些术语:
- 特征(Feature):反映数据内在规律的信息
- 特征和标记/目标(Label/Target)
- 用一个特征向量(Feature Vector)来描述一个数据样本
- 标记/目标的表现形式则取决于监督学习的种类
- 把这种既有特征,同时也带有目标/标记的数据集称作训练集(Training Set),用来训练我们的学习系统。
需要保证:出现在测试集中的数据样本一定不能被用于模型训练
2.用到的一些python库
2.1 NumPy&Scipy

2.2 Matplotlib

2.3 Scikit-learn

2.4 Pandas

3. 监督学习经典模型
任务的基本架构和流程:
准备训练数据->抽取所需要的特征,形成特征向量(Feature Vectors)->将特征向量连同对应的标记/目标(Labels)一并送入学习算法(Machine Learning Algorithm)->训练出一个预测模型(Predictive Model)->采用同样的特征抽取方法作用于新测试数据,得到用于测试的特征向量->使用预测模型对这些待测试的特征向量进行预测并得到结果(Expected Label)
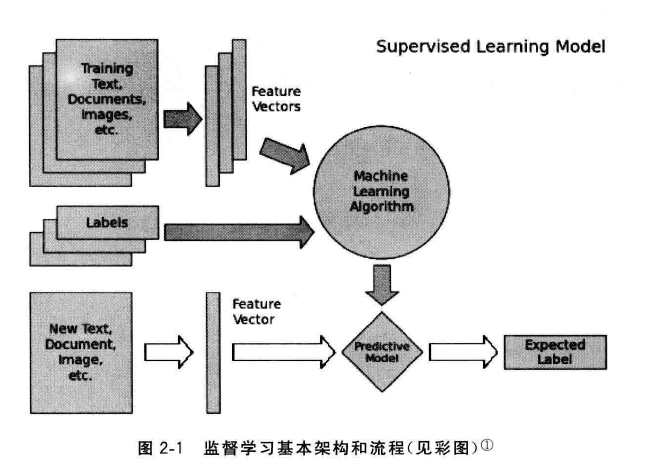
分类学习
- 二分类(Binary Classification)
- 多类分类(Multi-class Classification)
- 多标签分类(Multi-label Classification)
线性分类器(Linear Classifiers)
一种假设特征与分类结果存在线性关系的模型。通过累加计算每个维度的特征与各自权重的乘积来帮助类别决策。
定义\(\bold{x}=<x_1,x_2,\cdots,x_n>\)来代表\(n\)维特征列向量,同时用\(n\)维列向量\(\bold{w}=<w_1,w_2,\cdots,w_m>\)来代表对应的权重,或者系数(Coefficient);同时为了避免其过坐标原点这种硬性假设,增加一个截距(Intercept)\(b\)。由此这种线性关系可以表达为\(f(\bold{w},\bold{x},b)=\bold{w}^\mathrm{T}\bold{x}+b\),这里的\(f\in \mathbb{R}\),取值范围分布再整个实数域中。
所要处理的最简单的二分类问题\(f\in \{0,1\}\);因此需要一个函数把原先的\(f\in \mathbb{R}\)映射到\((0,1)\)。使用Logistic函数:$$\Large g(z)=\frac{1}{1+e^{-x}}$$
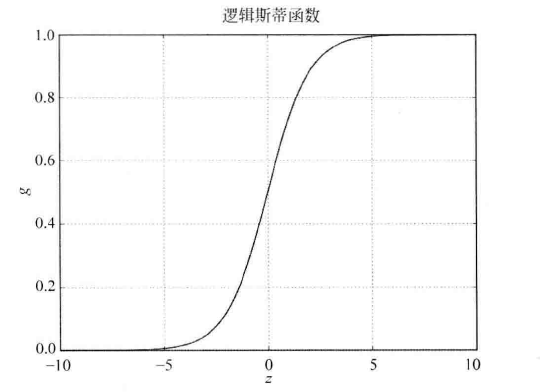
可以观察到该模型如何处理一个待分类的特征向量:
如果\(z=0\),那么\(g=0.5\);若\(z<0\)则\(g<0.5\),这个特征向量被判为一类;反之,若\(z>0\),则\(z>0\),则\(g>0.5\),其被归为另外一类。
综上,如果将\(z\)替换为\(f\),整合可得:经典的线性分类器,Logistic Regression:
\(\Large h_{\bold{w},b}(\bold{x})=g(f(\bold{w},\bold{x},b))=\frac{1}{1+e^{-f}}=\frac{1}{1+e^{-(\bold{w}^\mathrm{T}\bold{x}+b)}}\)

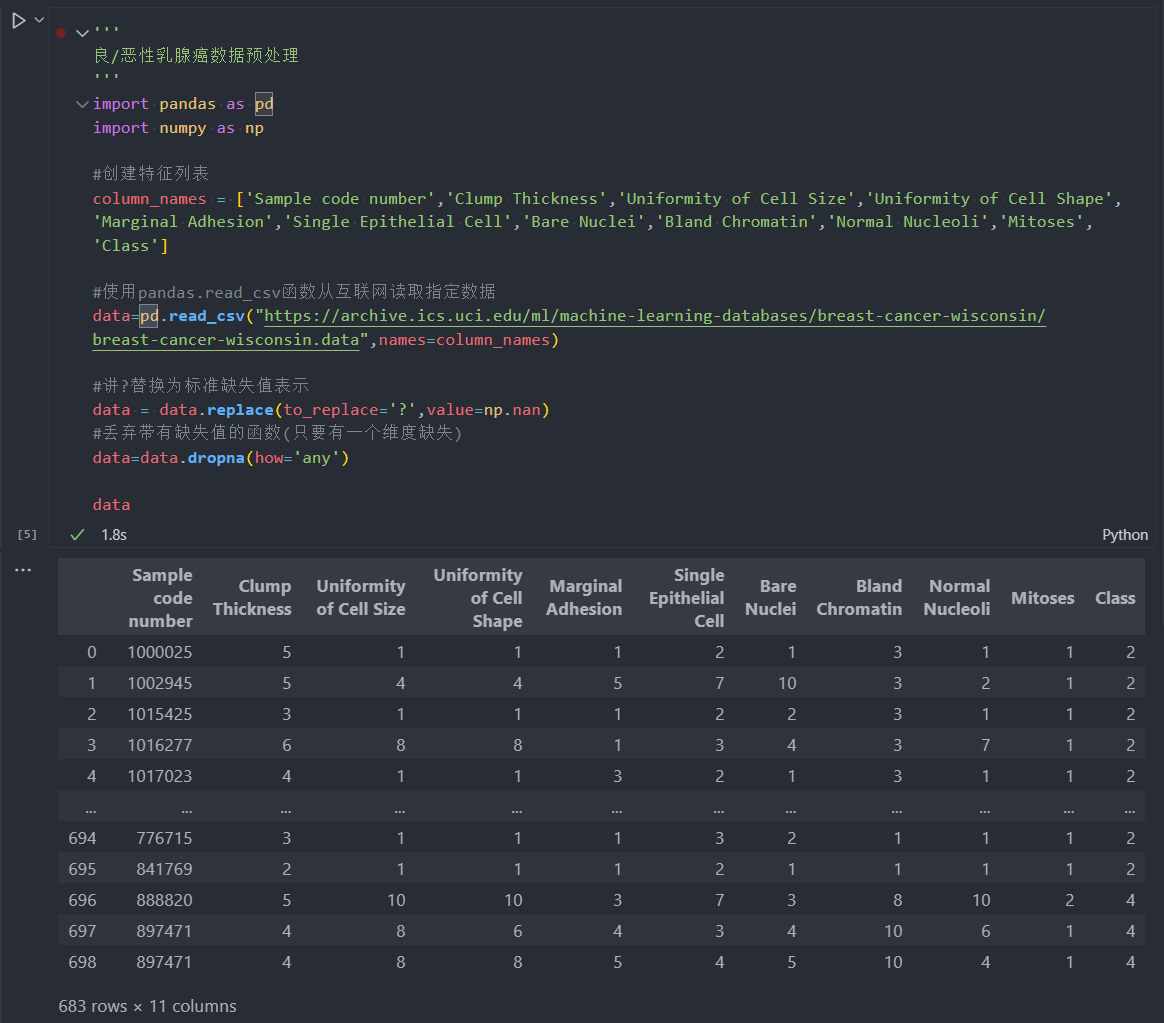
由于原始数据没有提供对应的测试样本用于评估模型性能,因此需要对带有标记的数据进行分割。通常情况下,25%的数据会作为测试集,其余75%的数据用于训练。
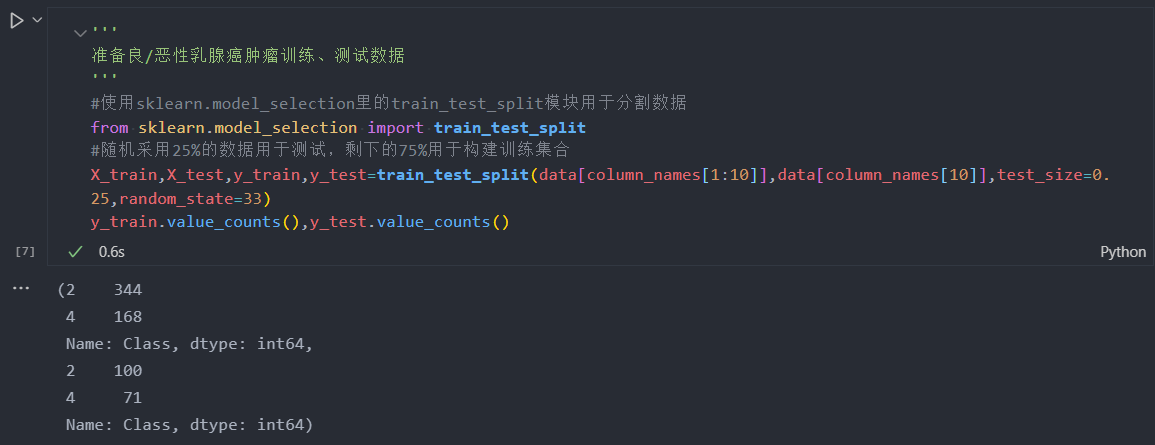
综上,用于训练样本共有512条(344条良性肿瘤数据、168条恶性肿瘤数据),测试样本有171条(100条良性肿瘤数据、71条恶性肿瘤数据)。
使用Logistic Regression和随机梯度参数估计两种方法对上述处理后的训练数据进行学习,并且根据测试样本特征进行预测。
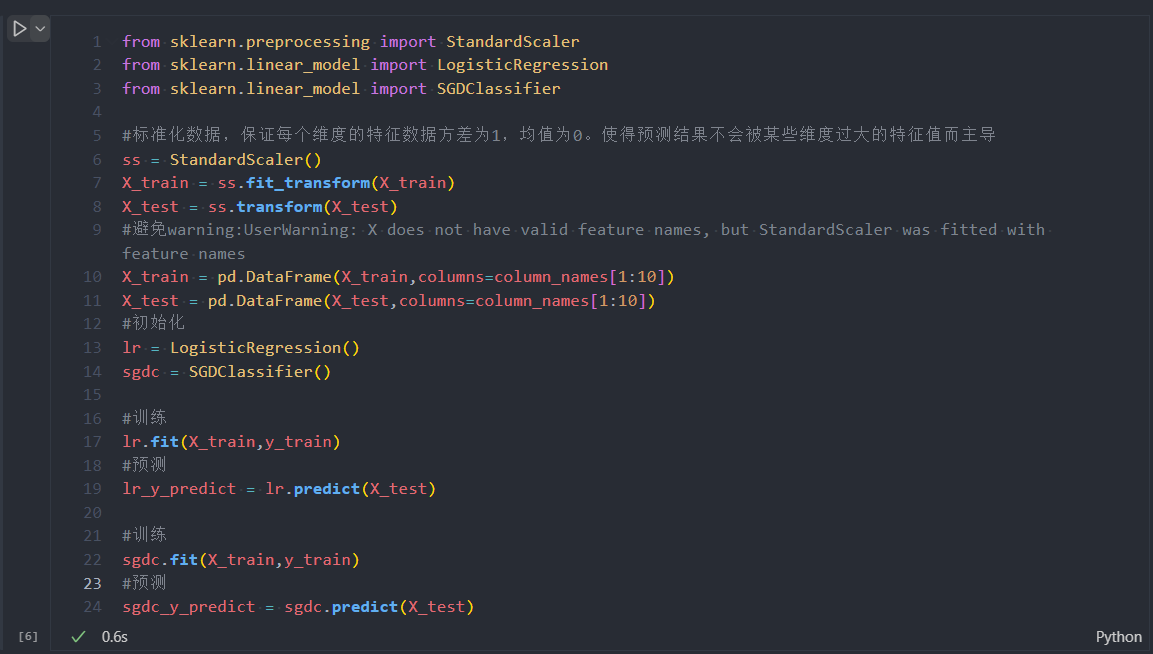
fit_transform和transform的区别:
fit_transform是fit和transform的组合fit(x,y)传两个参数的是有监督学习的算法,fit(x)传一个参数的是无监督学习的算法,比如降维、特征提取、标准化。fit和transform没有任何关系,之所以出来这么个函数名,仅仅是为了写代码方便,所以会发现transform()和fit_transform()的运行结果是一样的。- 注意:运行结果一模一样不代表这两个函数可以互相替换,绝对不可以!
transform函数是一定可以替换为fit_transform函数的,fit_transform函数不能替换为transform函数!
line 9 warning:
x由于经过了StandardScaler(),导致其被转化为了array格式,也就不存在feature names了。因此需要重新转回dataFrame并和feature names匹配。
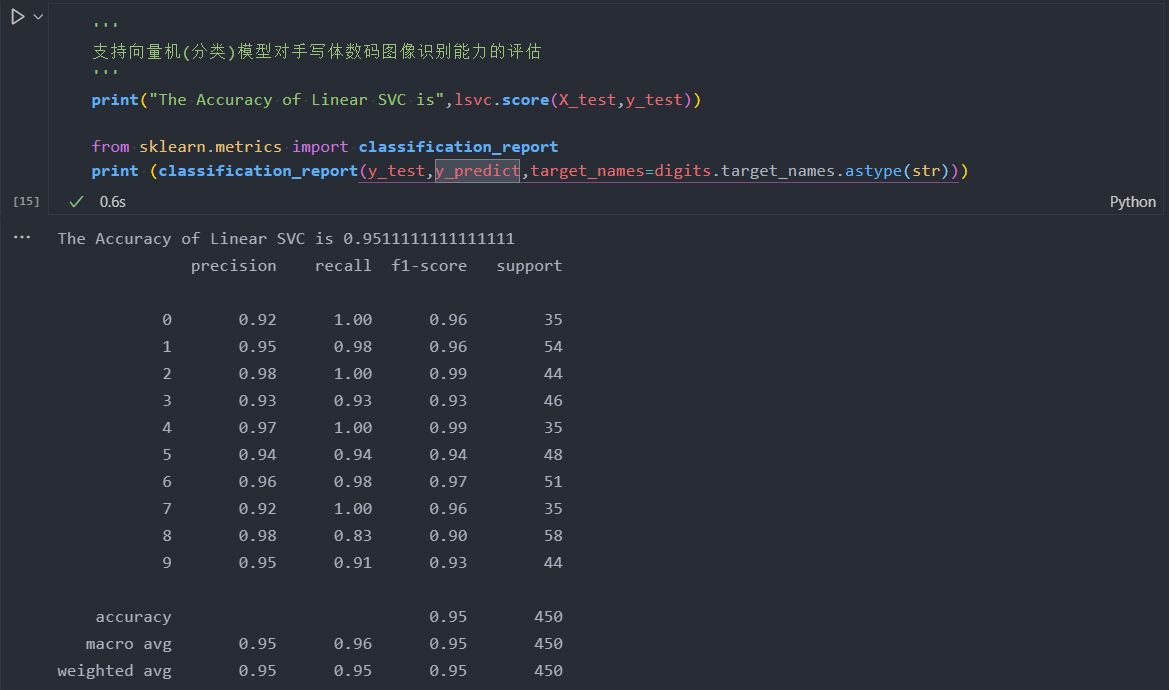
计算171条测试样本中,预测正确的百分比。将这个百分比称作准确性(Accuracy),并且将其作为评估分类模型的一个重要性能指标。
在二分类任务下,预测结果(Predicted Condition)和正确标记(True Condition)之间存在4种不同的组合,构成混淆矩阵(Confusion Matrix)。
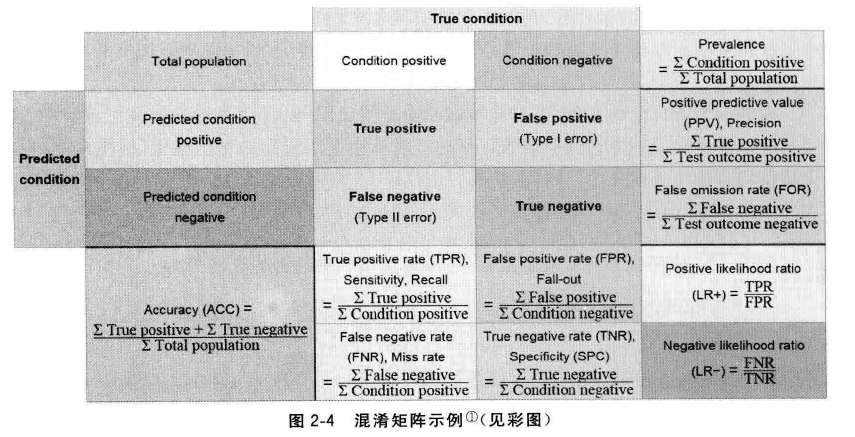
四个指标:
\(\Large准确性 \mathrm{Accuracy}=\frac{\#(\mathrm{True\,Positive})+\#(\mathrm{True\,Negative})}{\#(\mathrm{True\,Positive})+\#(\mathrm{True\,Negative})+\#(\mathrm{False\,Positive})+\#(\mathrm{False\,Negative})}\)
\(\Large精确率 \mathrm{Precision}=\frac{\#(\mathrm{True\,Positive})}{\#(\mathrm{True\,Positive})+\#(\mathrm{False\,Positive})}\)
\(\Large召回率 \mathrm{Recall}=\frac{\#(\mathrm{True\,Positive})}{\#(\mathrm{True\,Positive})+\#(\mathrm{False\,Negative})}\)
\(\mathrm{F1\,measure}\):\(\mathrm{F1}\)指标综合考量召回率与精确率
\(\Large \mathrm{F1\,measure}=\frac{2}{\frac{1}{\mathrm{Precision}}+\frac{1}{\mathrm{Recall}}}\)
采用调和平均数,是因为它除了具备平均功能外,还会对那些召回率和精确率更加接近的模型给予更高的分数。
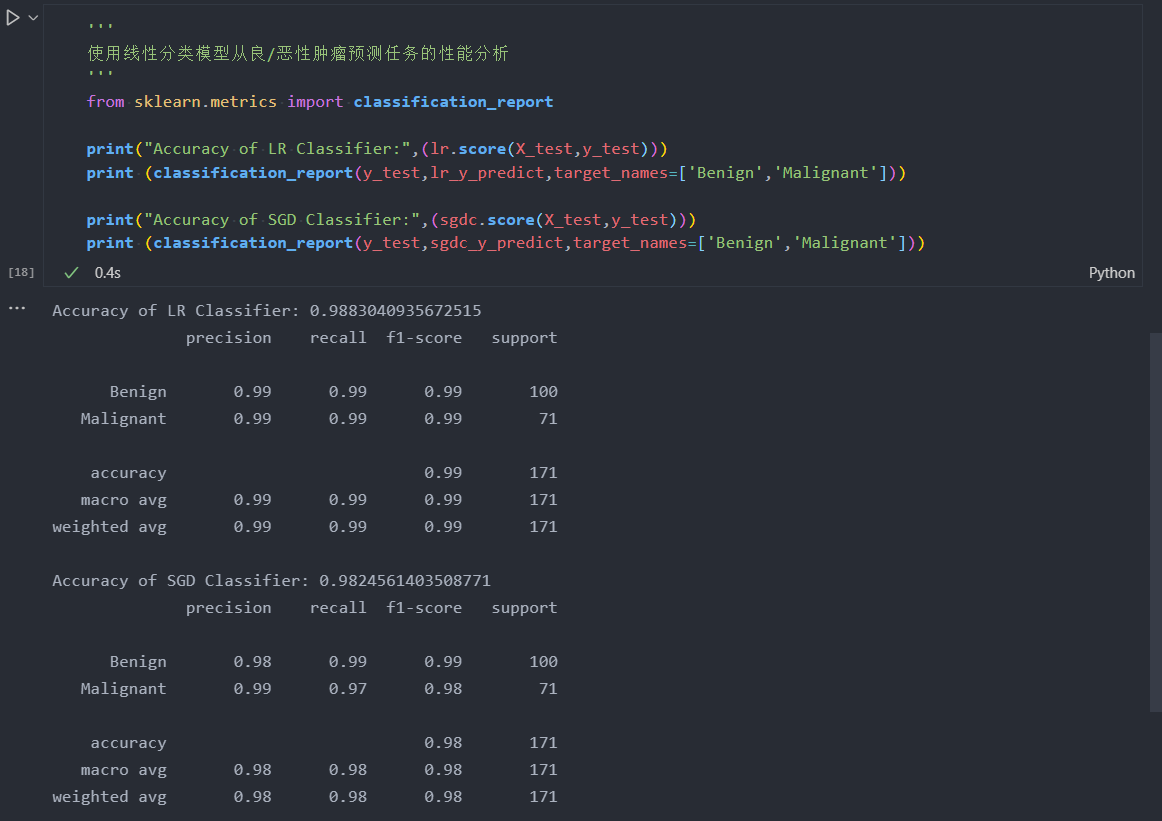
特点分析:
- 线性分类器可以说是最为基本和常用的机器学习模型。尽管其受限于数据特征与分类目标之间的线性假设,我们仍可以在科学研究与工程实践中把线性分类器的表现性能作为基准。这里所使用的模型包括Logistic Regression与SGD Classifier。
- 相比之下,前者对参数的计算采用精确解析的方式,计算时间长但是模型性能略高;后者采用随机梯度上升算法估计模型参数,计算时间短但是产出的模型性能略高。一般而言,对于训练数据规模在10万量级以上的数据,考虑到时间的耗用,笔者更加推荐使用随机梯度算法对模型参数进行估计。
支持向量机(分类)
在之前“良/恶性肿瘤肿瘤预测”的例子中,曾经使用多个不同颜色的直线作为线性分类的边界。同样,如图2-5所示的数据分类问题,我们更有无数种线性分类边界可供选择。
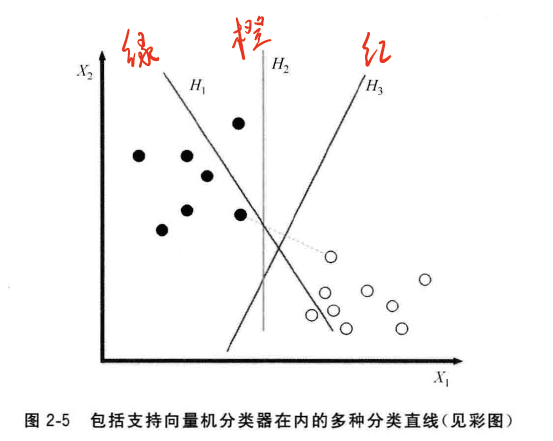
由于这些分类模型最终都是要应用在未知分布的测试数据上,因此我们更加关注如何最大限度地为未知分布地数据提供足够地待预测空间。
支持向量机分类器(Support Vector Classifier),便是根据训练样本地分布,搜索所有可能地线性分类器中最佳地那一个。根据图片我们会发现决定其直线位置的样本并不是所有的训练数据,而是其中的两个空间间隔最小的两个不同类别的数据点。
如果未知的待测数据也如训练数据一样分布,那么的确支持向量机可以帮助我们找到最佳的分类器。
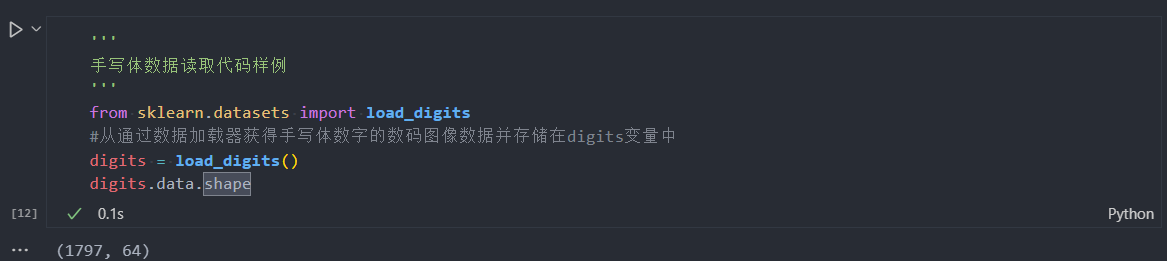
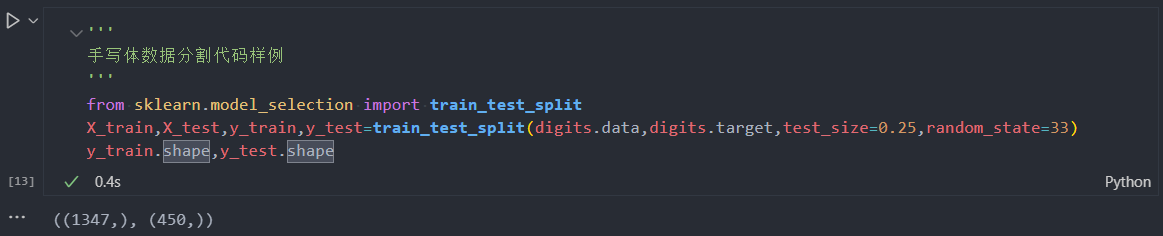
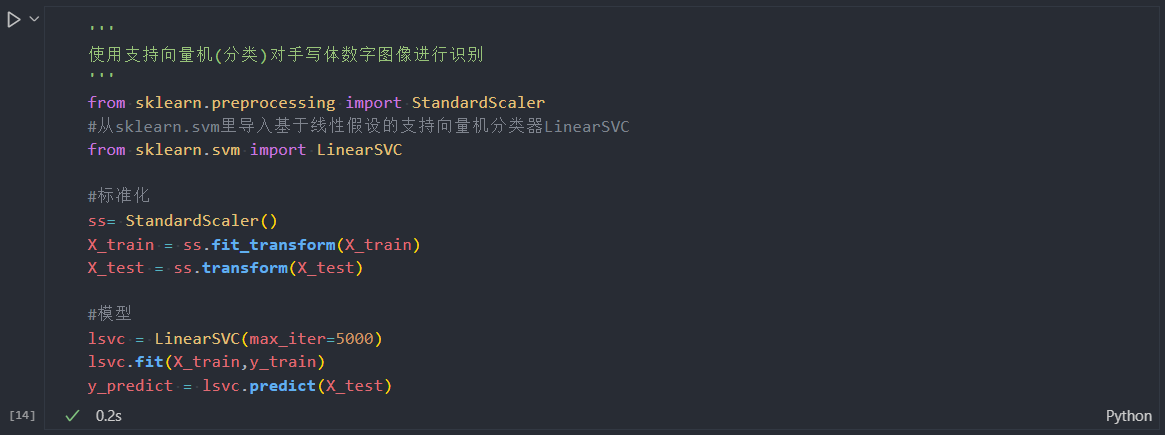
指出:
- 召回率、准确率和\(\mathrm{F1}\)指标最先适用于二分类任务;
- 逐一评估某个类别的这三个性能:我们把所有其他的类别看做阴性(负)样本,这样一来就创造了10个二分类任务。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号