联赛模拟测试16

T2 简单的序列

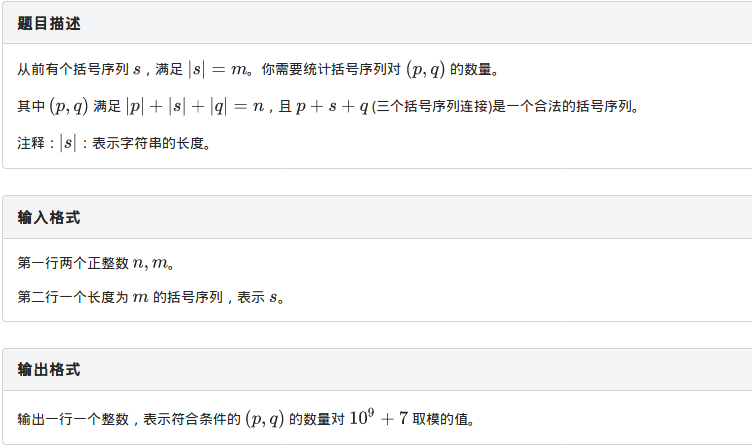
众所周知，这又是一道卡特兰数的题，但是小编又挂了，这已经是小编第三次挂在卡特兰数上了，这是怎么回事呢？原来是小编有一种情况没有考虑到，小编判断s集合括号匹配是这么判断的

for(int i=1;i<=m;++i)
    if(s[i]=='(')k++;
    else k--;

然后没有考虑到 )))((( 这种鬼情况，这种情况如果这么判断就挂了，然后就挂得只有 \(10pts\) ，我是暴力枚举，效率？？？可能是\((n-m)^2log_2(n-m)\)，但可能也不是，用 C++(NOI) + O2 就 T 成85，开 C++O2 就快了至少三倍（可能是我常数太大了）

首先先判断出原序列有多少个括号未匹配

for (int i = 1; i <= m; ++i) {
    if (s[i] == '(')k++;
    else k--;
    stt = (stt < k ? stt : k);
}

stt 表示有多少个 ')' 未匹配 k-stt 就是多少个 '(' 未匹配，然后枚举左右序列 p 和 q 中左右括号的数量，计算卡特兰数，相乘，就是结果

$ Code$

#include <bits/stdc++.h>
using namespace std;
#define gc getchar()
const long long mod = 1e9 + 7;
int n, m, k, sn, sm, stt;
char s[1000000 + 10];
long long v[1000000 + 10];

inline long long ksm(long long x, long long y) {
    register long long ans = 1;
    while (y) {
	if (y & 1)ans = ans * x % mod;
	y >>= 1;
	x = x * x % mod;
    }
	return ans;
}

inline long long C(long long n, long long m) {
    if (m == 0)return 1ll;
    return v[n] * ksm(v[m] * v[n - m] % mod, mod - 2) % mod;
}

inline void solve() {
    register int sn = -stt, sm = k - stt, pp;
    register long long ans = 0;
    pp = (n - m - sn - sm) >> 1;
    sn += pp, sm += pp;
    for (register int i = -stt; i <= sn; ++i)
      for (register int j = 0; j <= i + stt && j <= pp; ++j)
	    ans = (ans + (C(i + j, i) - C(i + j, j - 1)) % mod * (C(sn + sm - i - j, sm - j) - C(sn + sm - i - j, min(sn - i, sm - j) - 1)) % mod + mod) % mod;
    printf("%lld\n", ans);
}

inline void Solve() {
    sn = (n - m - k) >> 1;
    sm = n - m - sn;
    register long long x = min(sn, sm), ans = 0;
    for (int i = 0; i <= x; ++i)
		for (int j = 0; j <= i; ++j)
		    ans = (ans + (C(i + k + j, i + k) - C(i + k + j, j - 1)) % mod * (C(n - m - j - i - k, sn - j) - C(n - m - j - i - k, sn - j + 1)) % mod) % mod;
    printf("%lld\n", ans);
}

int main() {
    freopen("bracket.in", "r", stdin);
    freopen("bracket.out", "w", stdout);
    scanf("%d %d %s", &n, &m, s + 1), v[0] = 1;
    if (n % 2 == 1)return puts("0"), 0;
    for (int i = 1; i <= 300000; ++i)v[i] = v[i - 1] * i % mod;
    for (int i = 1; i <= m; ++i) {
	if (s[i] == '(')k++;
	else k--;
	stt = (stt < k ? stt : k);
    }
    if (stt < 0)solve();
    else Solve();
    return 0;
}