2.1 Motivation
2.1.1 Introduction
How to track the uncertainty of estimating Dynamical Systems over time, using Kalman Filter to perform these estimates.
(1)Linear Dynamical Systems
(2)Maximum-A-Posterior Estimation
(3)Nonlinear Variations
2.1.2 Kalman Filter Motivation
This week we will learn about the Kalman Filter for Bayesian estimation in robotics.
Kalman Filter is an optimal tracking algorithm for linear systems.
2.2 Kalman Filter Model
Learn the dynamics system and measurement models that underlie the common filter.
The dynamics system describes how the state of the object change in time, as well as how the robot measures the state.

To provide an estimate that captures this uncertainty, we will transform this dynamical model into a set of probability expression.
Now given both the dynamics system model and the probabilistic model, we can combine these two ideas.

Applying the Gaussian probability distribution model, both the state and the noise are represented with means and variances.

2.3 Maximum-A-Posterior Estimation
Bayesian Kalman Filter
- Apply the MAP to Bayesian' Rule
- Solve the maximization
- Establish Kalman Filter update method

通过最大化贝叶斯公式的后验概率求解卡尔曼模型,推导过程参见2-3附件材料。
卡尔曼滤波算法。注意下标表示的时序!
X(k)=A(k) X(k-1)+BU(k)+W(k) 状态运动方程
Z(k)=H (k)X(k)+V(k) 观测方程

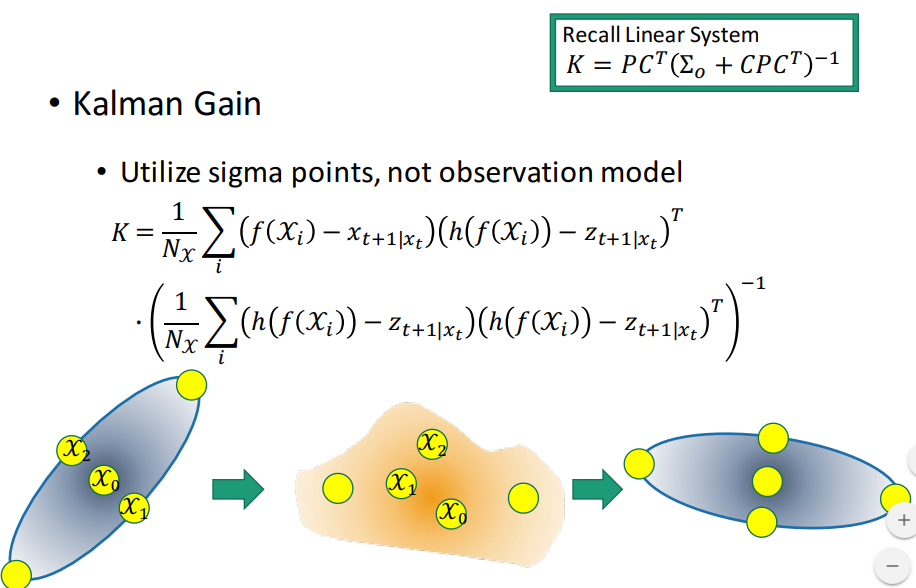
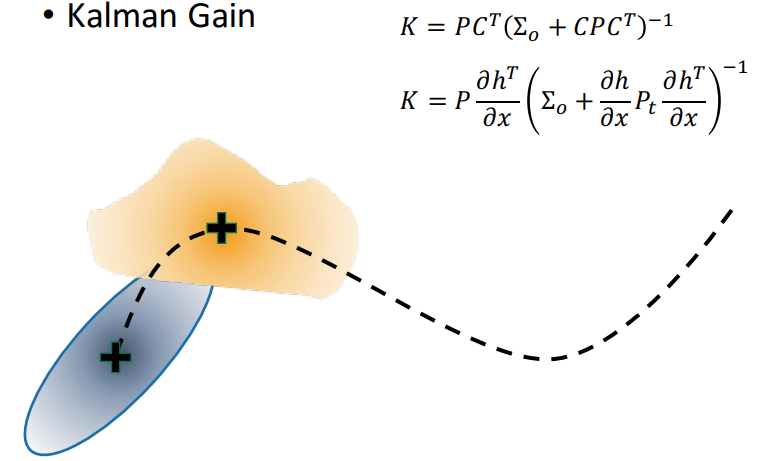
K 权衡预测协方差P和观测协方差矩阵R哪个更加重要。相信预测,残差(zt-Hxt)的权重小,相信观察,残差权重大,由 K 的表达可以推出这个结论
2.4 Non-linear Kalman filters
(1) Extended Kalman Filter
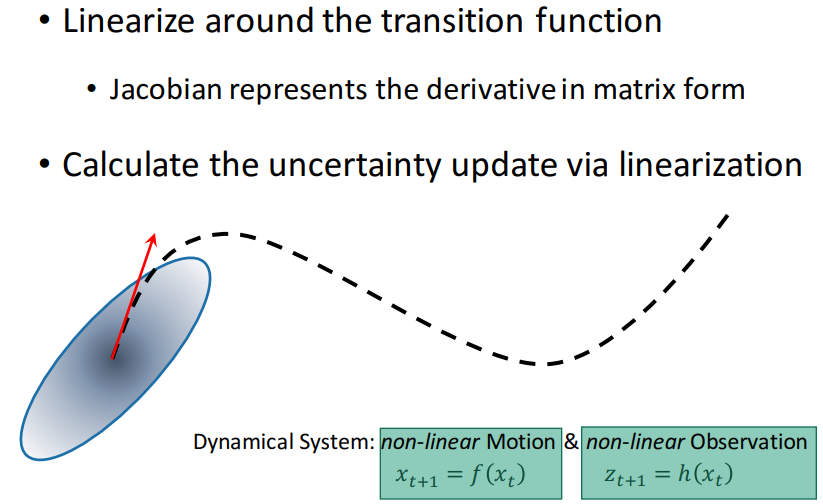
扩展卡尔曼滤波用于建模非线性系统(运动方程和观测方程为非线性方程)的不确定性。
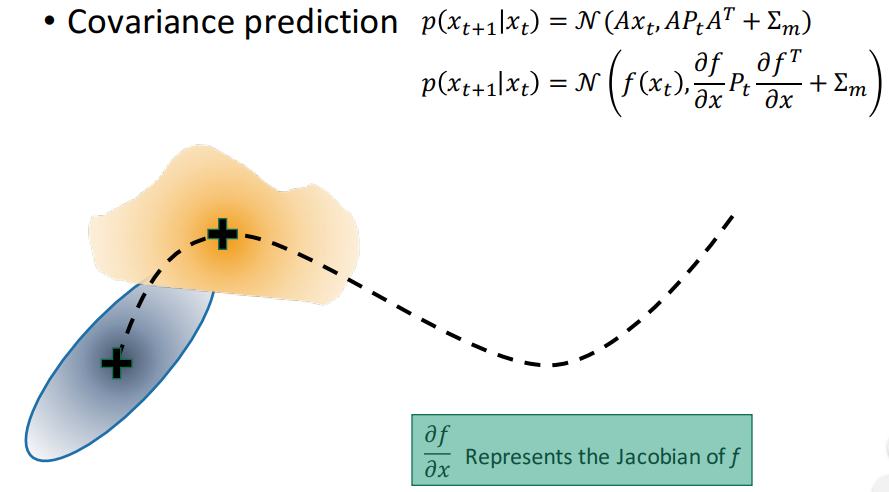
在非线性系统中,运动方程是状态的非线性函数。若运动方程可微,可以通过在当前时刻的线性化逼近来描述状态的变化。如果在未来一个时间步长中状态没有巨大的变化,线性逼近就可以是一个可行的追踪状态分布变化的方法。

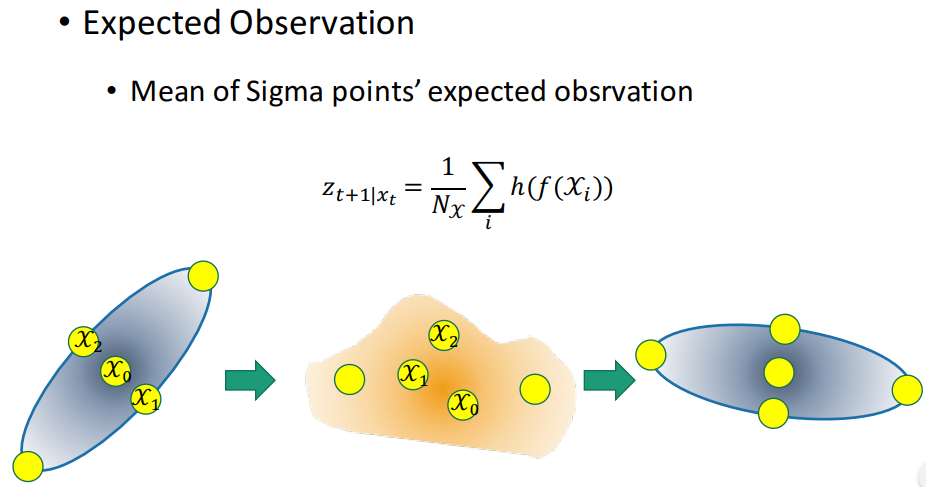
(2) Unscented Kalman Filter(UKF) 无损卡尔曼滤波
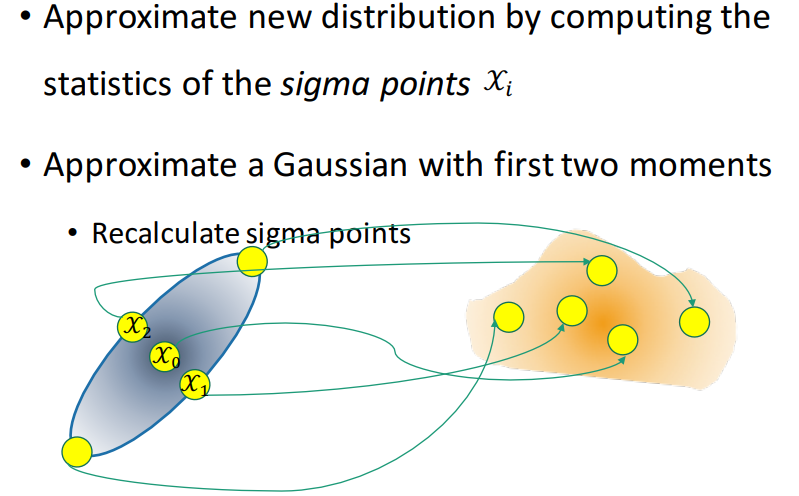
采用一组特征点,UKF不停地重估计分布的均值和协方差;
把特征点置于非线性动态系统中进行变换;
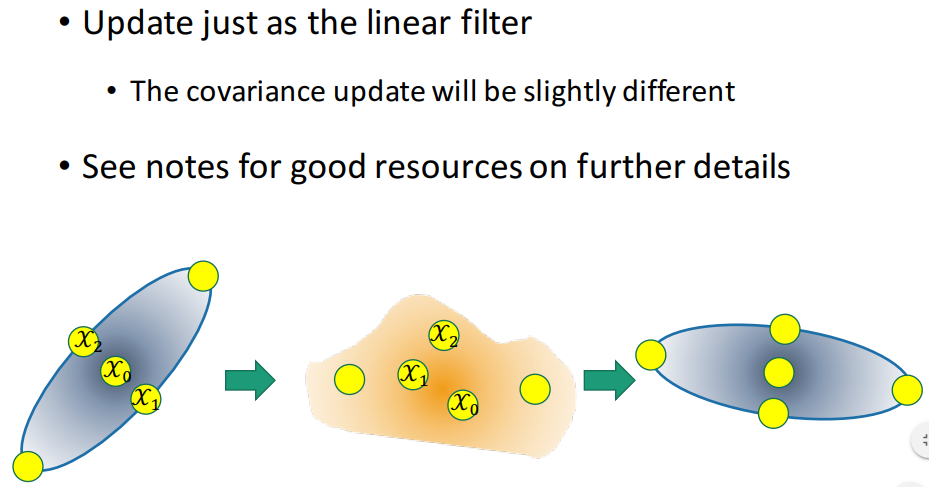
特征点满足高斯分布,但经过非线性转换后不再满足高斯分布。然而,可以通过重新计算均值和协方差来近似新的高斯分布。