算法第五章上机实践报告

算法第五章上机实验报告

一、回溯法分析

1.1 说明“最小重量机器设计问题”解空间

解空间：{{1，3，1}，{1，3，2}，{1，3，3}}

来源：对于第一个部件有三种选择，对于第二第三个部件同样有三种不同的选择，当列出所有解以后，按照满足题意要求小于d价格的条件筛选出来解空间。

1.2 说明 “最小重量机器设计问题"的解空间树

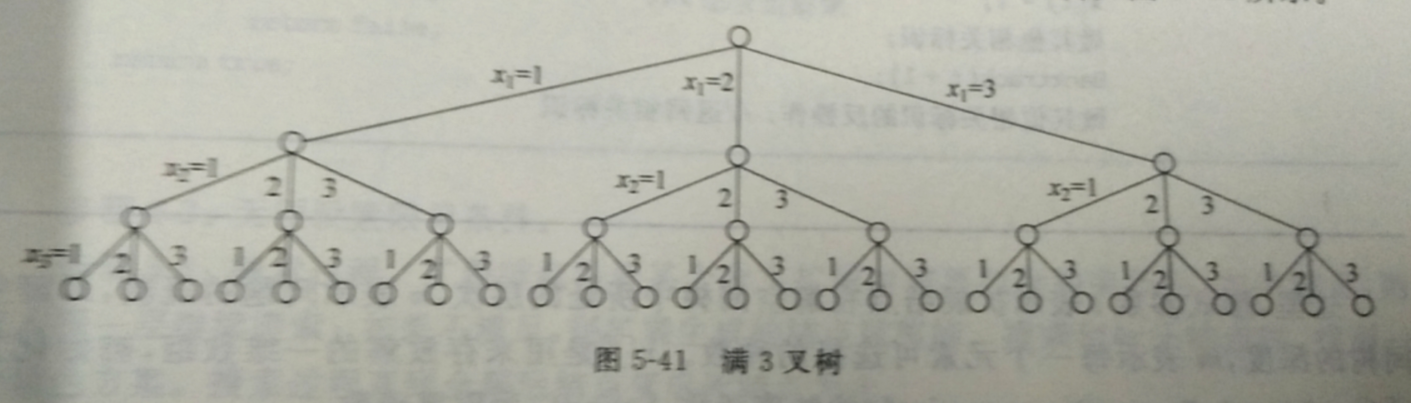
如图所示，问题的解空间树与之类似。

从第一个节点代表第一个部件，每个节点的边代表部件选择的供应商，因此每种情况下都有三种选择，然后在遍历过程依据条件进行剪枝。最后得到可行的解集

1.3在遍历解空间树的过程中，每个结点的状态值

在遍历解空间树的时候，每个每个节点的状态值就是当前层数（对应第几个部件）的选择的供应商以及到这个路径到目前位置累计的cw和cv。

二、我对回溯法的理解

代码实现

#include <iostream>

using namespace std;
int n,m,d;
int c[100][100];
int w[100][100];
int x[100]={0};
int p[100]={0};
int cv = 0,cw = 0 ;
int mw = 100000;

void backtrack(int t){
	if(t>n){ 
		if(cw < mw){
			mw = cw;
			for(int i=1;i<=n;i++){
			    p[i]=x[i];
		    }
		}
		return ;
	}
	for(int i=1;i<=m;i++){			
        cv += c[t][i]; 
		x[t] = i;
		cw += w[t][i];
		if(cv <= d && cw <= mw){
            backtrack(t+1);
		}			
            cv -= c[t][i]; 
			x[t] = 0;
			cw -= w[t][i];
	}
}

int main(){
	cin>>n>>m>>d;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin >> c[i][j];
		} 
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin >> w[i][j];
		} 
	}
	backtrack(1);
	cout<< mw<<endl;
	for(int i=1;i<=n;i++){
		cout<<p[i]<<" ";
	}
	cout<<endl;
}

理解收获：回溯法是利用计算机进行每一种情况进行遍历，以此来得到我们所需要的最终结果，在算法递归遍历的时候，我们需要进行剪纸操作，否则递归层数太多会导致运算时间过长。另外，回溯法每到达一次叶节点，就代表一个结果的出现，并且与理想结果比较，若是，则保存，若不是，则return进行回溯到上一个子问题所得到的结果然后进行再次遍历。回溯法根据需要我们要保存状态并记得状态修改。