结对项目
| 软件工程 | 网工1934 |
|---|---|
| 作业要求 | 点我查看 |
| 作业目标 | 实现一个自动生成小学四则运算题目的命令行程序,体验结对完成项目 |
结对成员:
蔡鑫源 3119005363 GitHub
罗汉光 3119005386 GitHub
一 PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 5 | 8 |
| Estimate | 估计这个任务需要多少时间 | 3 | 5 |
| Development | 开发 | 400 | 600 |
| Analysis | 需求分析 (包括学习新技术) | 300 | 360 |
| Design Spec | 生成设计文档 | 10 | 12 |
| Design Review | 设计复审 (和同事审核设计文档) | 5 | 4 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 30 | 45 |
| Design | 具体设计 | 360 | 400 |
| Coding | 具体编码 | 360 | 400 |
| Code Review | 代码复审 | 30 | 30 |
| Test | 测试(自我测试,修改代码,提交修改) | 120 | 120 |
| Reporting | 报告 | 60 | 70 |
| Test Report | 测试报告 | 30 | 25 |
| Size Measurement | 计算工作量 | 10 | 10 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 1743 | 2109 |
二、效能分析
生成一万道题并计算出答案的
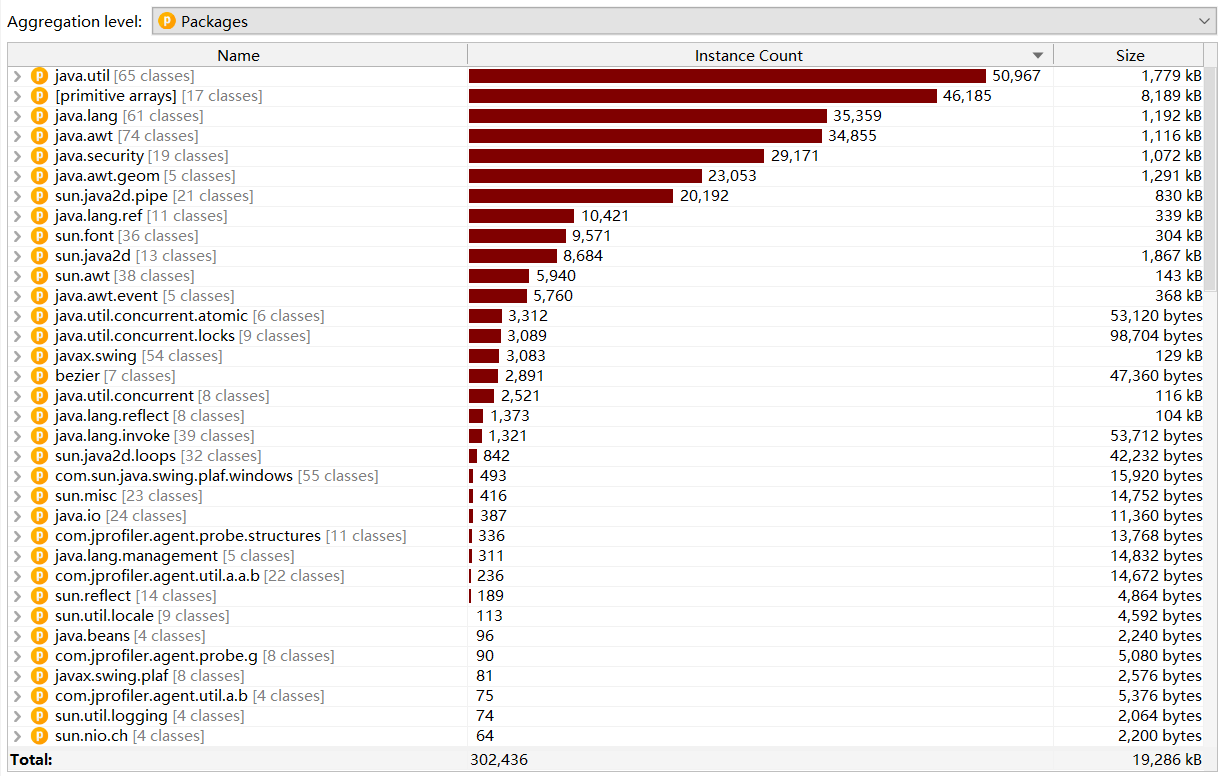
内存图为
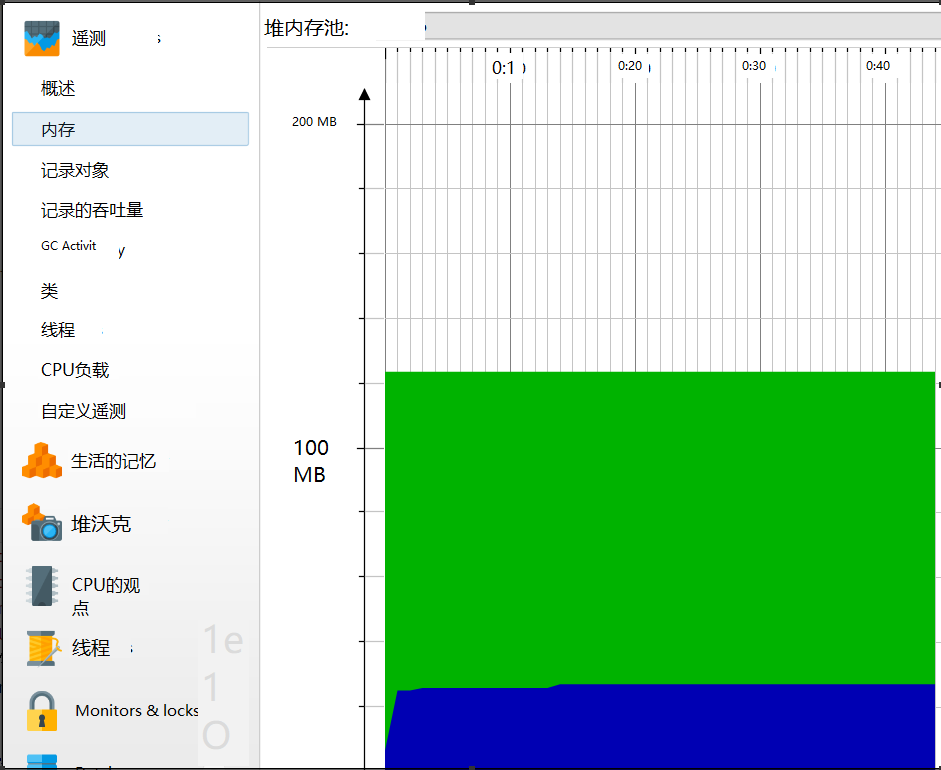
因为是采用了树的数据结构,可以看到占了一百多MB。
类图为
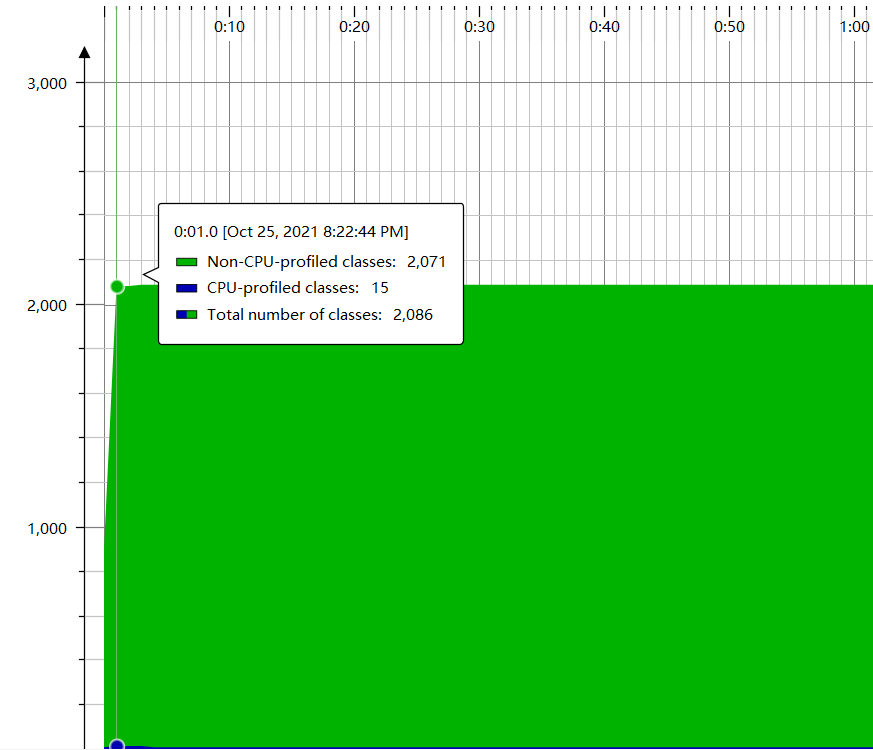
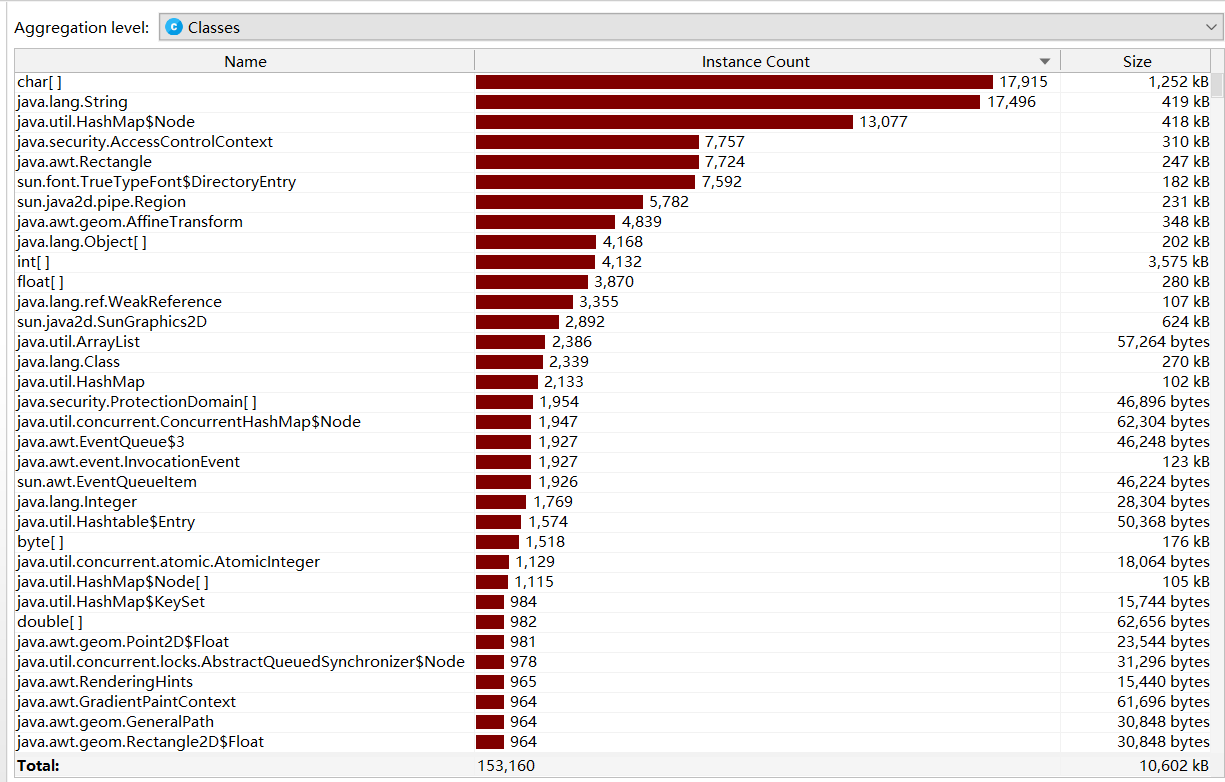
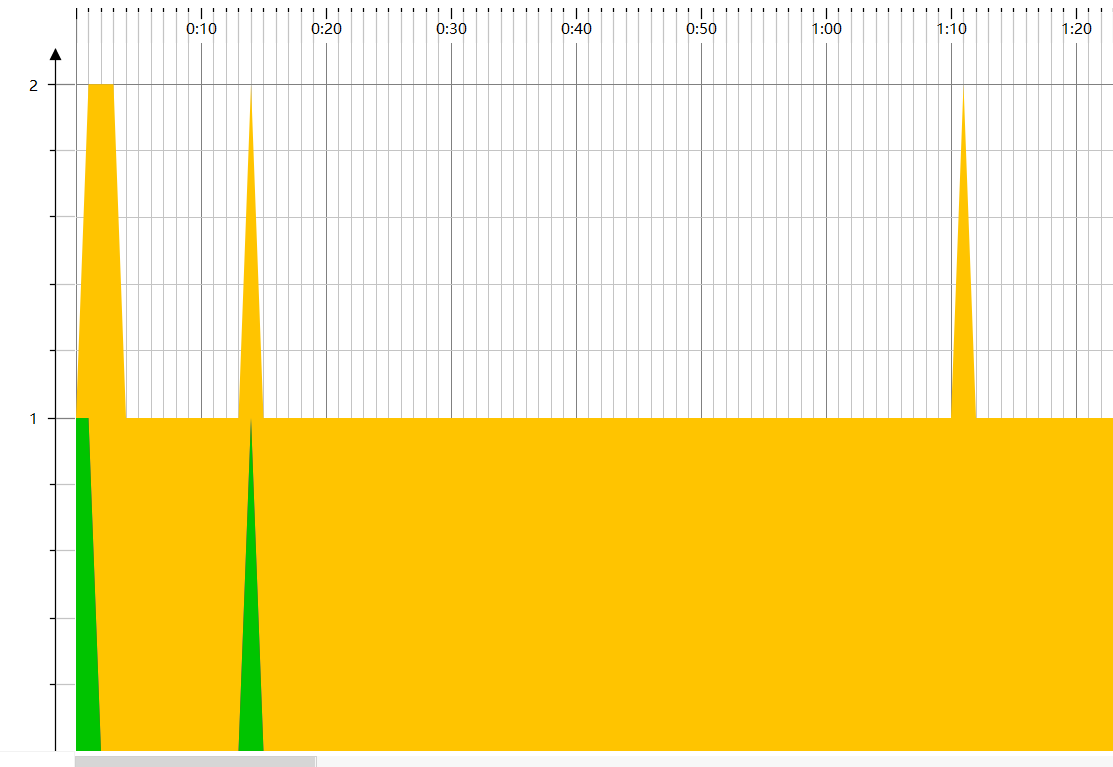
线程图
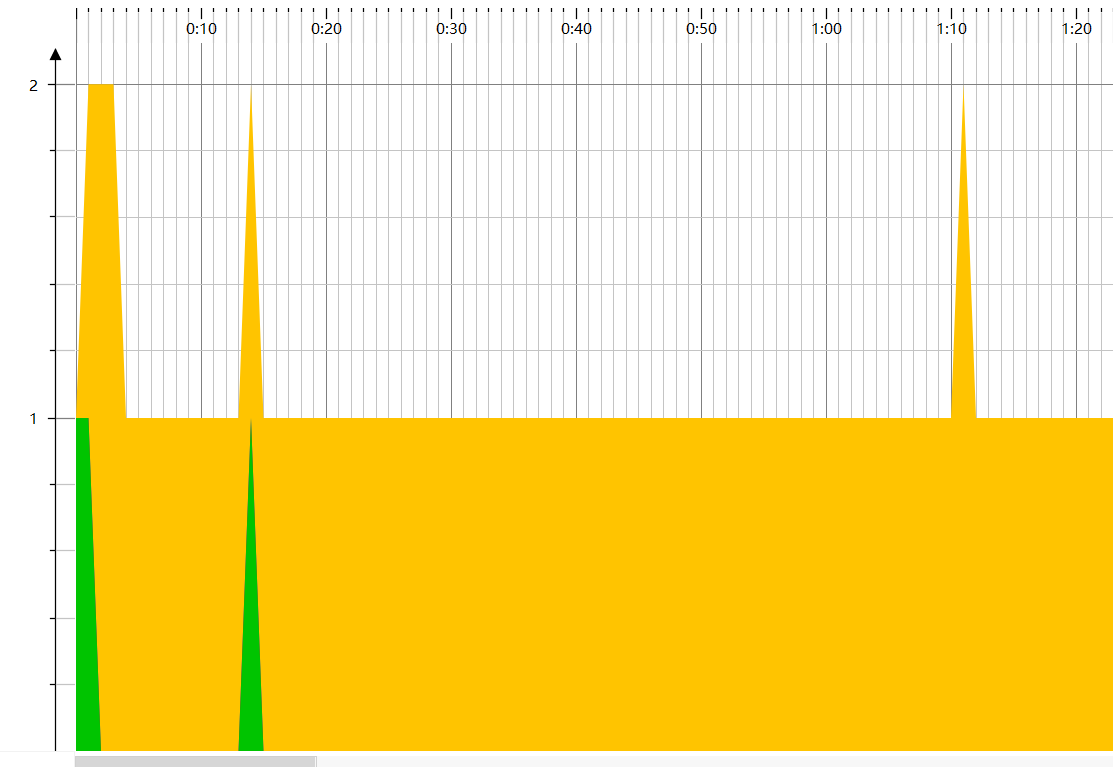
CPU负载
包图
三、设计实现过程
中缀表达式
人类最熟悉的一种表达式1+2,(1+2)3,3+42+4等等都是中缀表示法。对于人们来说,也是最直观的一种求值方式,先算括号里的,然后算乘除,最后算加减,但是,计算机处理中缀表达式却并不方便,因为没有一种简单的数据结构可以方便从一个表达式中间抽出一部分算完结果,再放进去,然后继续后面的计算(链表也许可以,但是,代价也是不菲)。
因此这里采用后缀表达式,即逆波兰表达式
逆波兰表达式
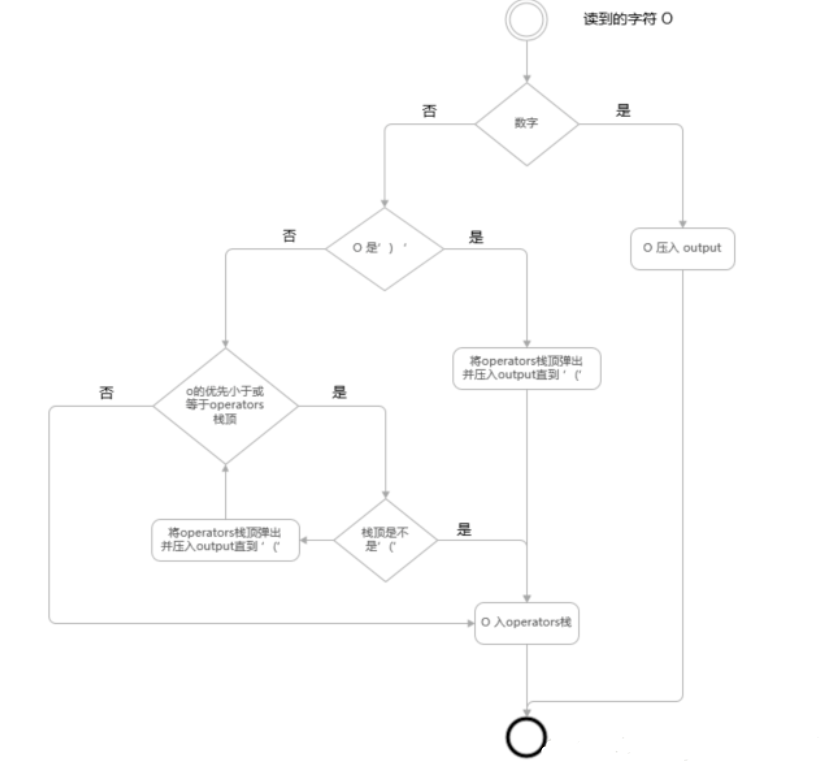
逆波兰表示法(Reverse Polish notation,RPN,或逆波兰记法),是一种是由波兰数学家扬·武卡谢维奇1920年引入的数学表达式方式,在逆波兰记法中,所有操作符置于操作数的后面,因此也被称为后缀表示法。逆波兰记法不需要括号来标识操作符的优先级。 编程实现的话,其实也很简单,两个栈即可实现,姑且把一个栈叫做 operators,保存运算符,另一个栈叫做output,保存最终的表达式。
就三个要点:
*数字直接入output
*运算符要与operators栈顶比较,优先级大则入栈,小于或等于则operators出栈后再入栈
*operators栈顶若是(则无条件入栈
其实逆波兰表达式相当于二叉树中的后序遍历,但是由于展示给用户看的不必用逆波兰表达式,用逆波兰表达式只是为了计算机更好的处理。而我们日常见到的式子中缀表达式其实相当于二叉树中的中序遍历,因此需要用到二叉树的数据结构以及相应的操作。
接下来介绍程序的实现过程
这个函数主要有五个类,分别是BinaryTree.java:这个类主要包括了
对二叉树的中序遍历函数:midTraversing()
判断表达式是否需要加括号函数:addBrackets(String operation1, String operation2, int leftOrRight)
以及重写了equals(Object obj)方法,判断两棵树是否一样(用于表达式判重)

Expression.class:这个类用于生成一个表达式,生成表达式的过程为:
首先产生一颗随机树generateBinaryTree(int maxNum, int operationNum),然后中序遍历这颗树即可得到表达式,具体过程可以看后续代码分析。同时这个类还包含了通过树来计算表达式结果的函数getResult(BinaryTree binaryTree)。
Fenshu.class:为了省去判断的步骤和代码的统一性,我们将所有的数字都化成分数来计算,在该类中,具有的功能有:随机生成一个分数newfenshu(int max),将整数化为分数intTofenshu(int num),以及分数的加减乘除运算函数,分数的约分函数maxCommonDivisor(int a, int b)等等。
nibolan.java:这个类主要用于将中缀表达式转化为逆波兰表达式,方便计算机操作,具体的过程上述已经讲到。
Main.java:主函数所在类,程序执行的入口,实现与用户的交互。
函数关系图如下
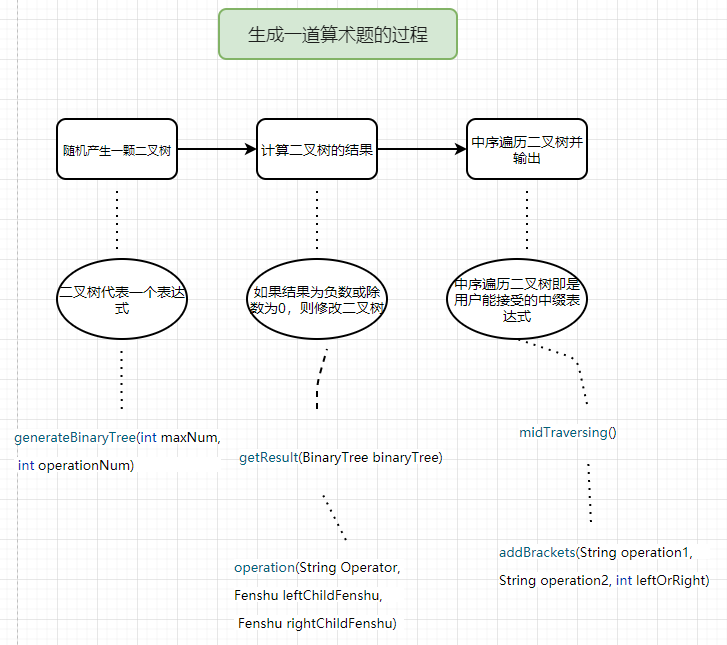
四、代码说明
对于这个项目,一个不能忽视的问题就是什么时候需要加括号,什么时候不需要加。
由运算法则,可以总结出加括号的规则如下:
1.当前节点的符号是减号,右子树的节点符号是加号或减号时,表达式右边需要加括号。
2.如果当前节点的符号是乘法,左右子树的节点是加法或减法,左右子树加括号。
3.如果当前节点的符号是除法,右子树如果是符号的话都加括号,左子树的符号是加法或减法加括号。
/**
* 判断是否需要加括号
*
* @param operation1 父结点运算符
* @param operation2 孩子结点运算符
* @param leftOrRight 1表示left,2表示right
* @return
*/
public static boolean addBrackets(String operation1, String operation2, int leftOrRight) {
if (operation2 == null) {
return false;
}
if (operation1.equals(operation[1])) { //父结点是“-”
if (operation2.equals(operation[1]) || operation2.equals(operation[0])) { //孩子结点是“+,-”
if (leftOrRight == 2) return true; //形如 a-(b-c)或a-(b+c),需加括号
}
}
if (operation1.equals(operation[2])) { //父结点是“*”
if (operation2.equals(operation[0]) || operation2.equals(operation[1])) {
return true; //形如(a-b)*c或(a+b)*c或a*(b-c)或a*(b+c),括号不可省略,需加
}
}
if (operation1.equals(operation[3])) { //父结点是“÷”
if (operation2.equals(operation[0]) || operation2.equals(operation[1])) {
return true; //同上
}
if (leftOrRight == 2) {
return true;
}
}
return false;
}
判断两棵二叉树是否是代表同一表达式,只需判断结点的分数或者运算符,以及左右孩子是否都是一致的,如果结点的运算符为加号或者乘号,还需交换左右子树进行判断,因为加法和乘法满足交换律。
/**
* 判断两棵树是否代表同一表达式
*
* @param obj
* @return
*/
@Override
public boolean equals(Object obj) {
if (obj != null) {
BinaryTree binaryTree = (BinaryTree) obj;
boolean l = false; //左孩子
boolean r = false; //右孩子
boolean f; //分数
boolean o; //符号
if (binaryTree.fenshu != null) {
f = binaryTree.fenshu.equals(this.fenshu);
} else {
f = this.fenshu == null;
}
if (binaryTree.opetation != null) {
o = binaryTree.opetation.equals(this.opetation);
} else {
o = this.opetation == null;
}
if (binaryTree.leftChild != null && binaryTree.rightChild != null && f && o) {
l = binaryTree.leftChild.equals(this.leftChild);
r = binaryTree.rightChild.equals(this.rightChild);
if (l == false && r == false && (binaryTree.opetation.equals(BinaryTree.operation[0]) || binaryTree.opetation.equals(BinaryTree.operation[2]))) {
r = binaryTree.rightChild.equals(this.leftChild);
l = binaryTree.leftChild.equals(this.rightChild);
}
} else {
l = this.leftChild == null;
r = this.rightChild == null;
}
return l && r && f && o;
} else {
return false;
}
}
表达式的生成代码,运算符的个数随机产生,为1-3个,且产生运算符个数的概率相等,然后再按这个运算符个数产生一颗随机的二叉树,产生二叉树的过程中,需要随机生成分数,为了避免大部分算式都包含分数,将分数出现的概率为1/3,二叉树产生完毕后,计算二叉树的运算结果,如果计算过程中出现除数为0,则将除号改为乘号,为什么不改成加号或减号呢,因为乘号跟除号是同级运算,如果换成加号或减号,则可能会产生括号缺乏问题,如果出现计算结果为负数,则交换左右子树,结果取相反数就变成整数了。
`public static final String Operators[] = {"+", "-", "×", "÷"};`
/**
* 按照限制的最大自然数随机生成表达式二叉树的构造方法
*
* @param maxNum
* @throws Exception
*/
public Expression(int maxNum) throws Exception {
//随机决定符号数量
int OperatorNum = (int) (Math.random() * 3) + 1;
tree = generateBinaryTree(maxNum, OperatorNum);
result = getResult(tree);
expression = tree.midTraversing() + " = ";
}
```
/**
* 随机生成二叉树
*
* @param maxNum
* @param operationNum
* @return
*/
public BinaryTree generateBinaryTree(int maxNum, int operationNum) throws Exception {
BinaryTree binaryTree = new BinaryTree();
if (operationNum == 0) {
//随机生成一个数
//判断是否生成分数,这里有1/3的概率生成分数 2/3的概率生成整数
boolean isfenshu = (int) (Math.random() * 3) == 0 ? true : false;
if (isfenshu) {
binaryTree.fenshu = Fenshu.newfenshu(maxNum);
} else {
binaryTree.fenshu = Fenshu.intTofenshu((int) (Math.random() * maxNum));
}
} else {
//随机生成一个运算符
binaryTree.opetation = Operators[(int) (Math.random() * 4)];
int leaveOperationNum = operationNum - 1;
int OperationNumToLeft = (int) (Math.random() * (leaveOperationNum + 1));
binaryTree.leftChild = generateBinaryTree(maxNum, OperationNumToLeft);
binaryTree.rightChild = generateBinaryTree(maxNum, leaveOperationNum - OperationNumToLeft);
}
return binaryTree;
}
/**
* 计算二叉树的结果
*
* @param binaryTree
* @return
* @throws Exception
*/
public Fenshu getResult(BinaryTree binaryTree) throws Exception {
if (binaryTree.leftChild == null && binaryTree.rightChild == null) {
return binaryTree.fenshu;
} else {
String operation = binaryTree.opetation;
Fenshu leftChildFenshu = getResult(binaryTree.leftChild);
Fenshu rightChildFenshu = getResult(binaryTree.rightChild);
//如果除数为0 则将除号改为乘号
if (operation == "÷" && getResult(binaryTree.rightChild).toString().equals("0")) {
binaryTree.opetation = "×";
operation = "×";
}
binaryTree.fenshu = operation(operation, leftChildFenshu, rightChildFenshu);
//若结果为负数,左右子树交换,值取绝对值
if (binaryTree.fenshu.getfenzi() < 0) {
binaryTree.fenshu.setfenzi(Math.abs(binaryTree.fenshu.getfenzi()));
BinaryTree node = binaryTree.leftChild;
binaryTree.leftChild = binaryTree.rightChild;
binaryTree.rightChild = node;
}
return binaryTree.fenshu;
}
}
逆波兰表达式的实现过程前面已经说过,这里展示代码部分
public class nibolan {
public static String rpn(String str) {
Stack<Character> operators = new Stack<>();
Stack output = new Stack();
char[] chars = str.toCharArray();
int pre = 0;
boolean digital; //是否为数字(只要不是运算符,都是数字),用于截取字符串
int len = chars.length;
int bracket = 0; // 左括号的数量
for (int i = 0; i < len; ) {
pre = i;
digital = Boolean.FALSE;
//截取数字
while (i < len && !Operator.isOperator(chars[i])) {
i++;
digital = Boolean.TRUE;
}
if (digital) {
output.push(str.substring(pre, i));
} else {
char o = chars[i++]; //运算符
if (o == '(') {
bracket++;
}
if (bracket > 0) {
if (o == ')') {
while (!operators.empty()) {
char top = operators.pop();
if (top == '(') {
break;
}
output.push(top);
}
bracket--;
} else {
//如果栈顶为 ( ,则直接添加,不顾其优先级
//如果之前有 ( ,但是 ( 不在栈顶,则需判断其优先级,如果优先级比栈顶的低,则依次出栈
while (!operators.empty() && operators.peek() != '(' && Operator.cmp(o, operators.peek()) <= 0) {
output.push(operators.pop());
}
operators.push(o);
}
} else {
while (!operators.empty() && Operator.cmp(o, operators.peek()) <= 0) {
output.push(operators.pop());
}
operators.push(o);
}
}
}
//遍历结束,将运算符栈全部压入output
while (!operators.empty()) {
output.push(operators.pop());
}
StringBuilder s = new StringBuilder();
while (!output.empty()) {
s.append(output.pop() + " ");
}
return s.reverse().toString();
}
}
enum Operator {
ADD('+', 1), SUBTRACT('-', 1),
MULTIPLY('*', 2), DIVIDE('/', 2),
LEFT_BRACKET('(', 3), RIGHT_BRACKET(')', 3); //括号优先级最高
char value;
int priority;
Operator(char value, int priority) {
this.value = value;
this.priority = priority;
}
/**
* 比较两个符号的优先级
*
* @param c1
* @param c2
* @return c1的优先级是否比c2的高,高则返回正数,等于返回0,小于返回负数
*/
public static int cmp(char c1, char c2) {
int p1 = 0;
int p2 = 0;
for (Operator o : Operator.values()) {
if (o.value == c1) {
p1 = o.priority;
}
if (o.value == c2) {
p2 = o.priority;
}
}
return p1 - p2;
}
/**
* 枚举出来的才视为运算符,用于扩展
*
* @param c
* @return
*/
public static boolean isOperator(char c) {
for (Operator o : Operator.values()) {
if (o.value == c) {
return true;
}
}
return false;
}
}
其他代码比较简单,也有备注,有兴趣的话可以去github看看源代码。
五、测试运行
Expression(int maxNum)函数测试,按照限制的最大自然数随机生成表达式二叉树的构造方法,maxNum为最大自然数
测试代码
Expression e1 =new Expression(1);
Expression e2 =new Expression(2);
Expression e3 =new Expression(3);
Expression e4 =new Expression(4);
Expression e5 =new Expression(5);
Expression e6 =new Expression(6);
Expression e7 =new Expression(7);
Expression e8 =new Expression(8);
Expression e9 =new Expression(9);
Expression e10 =new Expression(10);
System.out.println(e1.getExpression());
System.out.println(e2.getExpression());
System.out.println(e3.getExpression());
System.out.println(e4.getExpression());
System.out.println(e5.getExpression());
System.out.println(e6.getExpression());
System.out.println(e7.getExpression());
System.out.println(e8.getExpression());
System.out.println(e9.getExpression());
System.out.println(e10.getExpression());
测试结果
``Expression.equals(Object obj)测试,判断两个表达式是否是同一个。
测试代码
Expression e1 =new Expression("1 + 2 × 3");
Expression e2 =new Expression("1 × 2 + 3");
Expression e3 =new Expression("1 + 2 × 3");
Expression e4 =new Expression("1 + 3 × 2");
Expression e5 =new Expression("2 + 3 + 1");
Expression e6 =new Expression("1 + 3 - 2");
Expression e7 =new Expression("1 - 2 + 3");
Expression e8 =new Expression("1 ÷ ( 3 + 2 ) ");
Expression e9 =new Expression(" ( 1 ÷ 3 ) + 2");
Expression e10 =new Expression("1 ÷ 3 + 2");
System.out.println("e1 = e2 ?"+e1.equals(e2));
System.out.println("e1 = e3 ?"+e1.equals(e3));
System.out.println("e1 = e4 ?"+e1.equals(e4));
System.out.println("e2 = e3 ?"+e2.equals(e3));
System.out.println("e2 = e4 ?"+e2.equals(e4));
System.out.println("e3 = e4 ?"+e3.equals(e4));
System.out.println("e1 = e5 ?"+e1.equals(e5));
System.out.println("e6 = e7 ?"+e6.equals(e7));
System.out.println("e8 = e9 ?"+e8.equals(e9));
System.out.println("e8 = e10 ?"+e8.equals(e10));
System.out.println("e9 = e910 ?"+e9.equals(e10));
测试结果,可以发现与预期结果一致,但要注意输入的测试用例中符号与数字之间保持空格。
程序测试
首先测试生成十道题目,并检查结果是否正确,输入参数如下
运行结果如下图,可以看到生成并计算十道题所花的时间为6ms。

接着测试评判是否正确,输入如下参数

执行结果




可以看到结果符合预期。
接下来测试生成一万道题目



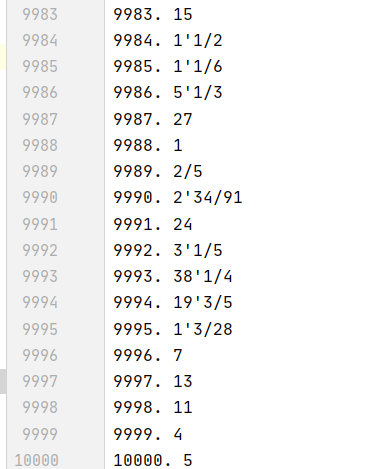
程序执行时间仅为67ms,这多亏了程序中二叉树和栈的数据结构。
六、项目小结
罗汉光:这次的作业是室友和我搭档完成的。一拿到这个作业,有点不知道从何处开始下手。于是我们先分析有哪些难点,比如:需要处理真分数,括号,空格;生成表达式;判断表达式是不是同一个题目等等。面对这么多问题,我们决定先解决生成表达式的问题,毕竟必须有了表达式才能完成后面的步骤。通过查阅资料,我们发现利用好二叉树的特性能很好地解决生成表达式的问题。接着是运算的问题,我们想到把每个数统一用分数来表示,为此我们特定写了一个Fenshu类来表示每个数,接着使用逆波兰表达式来计算。对于判断表达式是不是同一个题目的问题,我们先列举多个属于同一个题目的例子,从中观察,总结规律,找到了判断的方法。
整个过程中,我们从一开始的不知从何下手到一步一步解决问题,共同成长。我们总结一些方法:面对问题,可以先把它拆分,找出简单的,重要的部分先解决;同时需要多交流想法,找发现问题。整个过程中困难较大的是debug部分,因为遇到一些例子而不得不推翻之前的方法。总之,这次的作业收获还是挺多的。
蔡鑫源:刚看到这个作业的时候,觉得不是很难,而且是和搭档一起完成的,应该用不了多少时间就能做出来。但是开始做的时候,和伙伴讨论具体实现细节时却发现有不少棘手的问题,比如题目判重的算法,括号的判定,答案的校对等等。这些对我来说都是算比较大的问题了,如果是我一个人估计难以在短时间解决,但是两个人一起完成一个项目真的比一个人完成好很多,可以互相交换想法和思路,可以即使指出对方想法的不足之处,可以相互取长补短,面对一个问题可以两个人一起讨论各种解决方法然后再筛选出最佳的解决方案,我认为这比个人项目要更加享受得多。在这次结对完成项目的过程中,我学习到了不少需要补充的知识,也能够以新的思路去思考解决问题,两个人一起做的过程中遇到bug能较快的找出问题所在,一个问题一个问题解决完后,收获了不少。但是我觉得我们也有不足的地方,急于下手,较少的考虑了可行性,导致有些努力都付之东流了,希望下次团队合作能够更好。


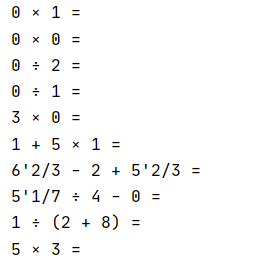



 浙公网安备 33010602011771号
浙公网安备 33010602011771号