数组

        数组是一种线性表，用连续的内存空间来存放相同的类型的数据。

        1.1 数组是一种线性表

        线性表，元素之间的关系，可以连成一条线的就叫做线性表，它们的关系是简单的前后关系。比如常见的，链表，栈，队列等等

        非线性表，元素之间不是简单的前后关系，比如，树和图。

        1.2 连续的内存空间和相同类型的数据

         正是因为这两个限制，它才有堪称杀手级的特性，随机访问。但是这两个限制也让

         数组很多操作都变得非常低效，比如要想在数组中删除，插入一个数据，为了保证连续性 ，就要做大量的数据迁移工作

       1.3 数组低效的插入和删除操作。

         第一次学习数据结构的时候，老师和我说，链表和数组的区别是什么呢，链表的插入和删除效率比数组高。

         数组的查找效率更好（数组支持下标访问，根据下标随机访问的时间复杂度为O(1））。

         老师和我们说，为了保证内存空间的连续性，比如你在数组中插入一个元素，那么所有的数据都要往后移动一位。

         所以它的时间复杂度是o(n);当时也没怀疑老师的说法，也没去想想有没有什么解决方案，真是惭愧...

         现在静下心来想想，还真有解决办法。因为这里的问题就是：数据大规模的搬移工作。

         如果说，我们在插入数据的时候，直接将第n个位置上 的数组，移动到数组元素最后，把新元素直接放入第K个位置。

         这样时间复杂度就是o(1);

          

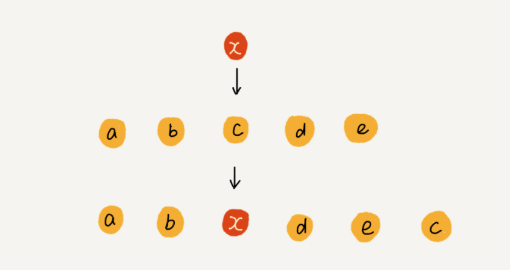
           如上图所示；

           再来看看删除操作

          删除一个数据，为了内存的连续性，也要搬移数据，不然就会出现空洞，内存就不连续了。

          实际上在某些特殊的场景下，我们不一定非得追求数组中，数据的连续性。如果我们将多次删除操作，集中到一起执行

          效率是不是会提高很多呢。

         现在要删除依次a,b,c这个三个元素，为了避免d，e,f,g,h这几个数据被移动三次，我可以先记录下已经删除的数据。

         每次删除的操作并不是真正的搬移数据，而是记录数据已经被删除。当数组没有更多的空间存储数据的时候，再触发一次

         真正的删除操作，这样就大大的减少了删除操作导致的数据搬移。

         1.4  数组的越界问题，很多高级语言都已经对这个进行包装了，数组越界会抛出异常。

         1.5 C#里面ArrayList,数组，List的区别。面试题常考。

         1.6 数组里面的连续存储空间对CPU来说是非常友好的，因为它可以借助CPU缓存机制，按照如果这个内存块被用到，则他下一个内存块也会有很大可能被用到的原则，所以CPU把数据加载到CPU的缓存的时候，会考虑把连续的空间一起加入缓存中。