复杂度分析（一）

  （一） 复杂度分析的由来

     我们平时写代码的时候，想要知道一段代码的运行时间，占用空间等等，一般都是在代码开始的记录一下当前时间，运行结束的时候，再记录一下时间，最后得出这段代码的运行时间，一般就是通过这个来判断我们的代码的执行效率。这种做法没有错，但是这样做统计出来的。

      在我之前写业务代码的时候，比如增删查改的时候，我经常都是这么干的，为了让一个查询更快，更有效率，边调试，边分析，找出慢的步骤，再逐一解决。那么问题来了，我们还需要学这个算法的时间复杂度分析吗？

      对于这个问题，之前我也是很茫然，看到算法时间复杂度分析的相关内容，我就直接忽略，想着工作中也不会这么分析。

      那么，我先解释一下，上面这种做法有什么弊端呢（其实上面的做法，真心还行）。 1、我们通过这种代码得出来的运行时间是很依靠机器的硬件的，要看你CPU的计算能力，内存的大小等等（不是很多时候，都会有这么一个情况，线下测试很快，线上慢成狗了，因为没有考虑到CPU的分配情况，内存占用情况）。2、这种统计方法受到数据规模的影响很大，在测试环境，测得再OK，上线之后还是问题很大）。

     基于上面这些问题，IT的大牛们，就想了一下，要不对算法的时间复杂度来个抽象，不要依赖于机器，硬件等等做法呢。所以他们就提出了一种做法就做O(n)，时间复杂度做法。

 （二）什么是时间复杂度O(n）

      时间复杂度：它并不是表示代码的真正运行时间，而是表示代码的执行时间随数据规模增长的变化情况。

      下面来看这个例子。

    int GetSum(int n)
    {
    1       var sum = 0;
    2       for (var i = 0; i < n; i++)
            {
    3             sum += i;
            }
            return sum;
   }

         我们知道每个语句的执行操作，从CPU的角度来看，就是读数据--运算--写数据，假设这整个操作需要一个单位的时间。我们假设一行代码就是一个单位的执行时间，那么这段代码就是2+2n个单位时间，从这里可以看出来程序的执行时间是和n成正比的。我们把这个规律总结成为一个公式，就是我们的时间复杂度。

    （三）时间复杂度的分析方法

          1、关注执行次数最多的那段代码，那个就是这整段代码的时间复杂度

          2、乘法法则，两个时间复杂度相乘，就是整个时间复杂度。（嵌套内外代码的复杂度等于内外复杂度的乘积）

          3、总的复杂度等于最大的那个复杂度。（一般两个复杂度，不是同一个层级的时候，才取最大的，比如o(n)和o(n2),则取o(n2)，如果一个是o(n),另外一个是o(m),则时间复杂度就是o(m+n)）

      (四）总结

           感觉这个时间复杂度分析，就像设计模式，你说按照设计模式写出来的代码，也不一定是最好的。我们时间复杂度也是一样，也不一定说o(n)就比o(n2)的好，但是只要当我们一提到某某某设计模式的时候，心里马上就可以勾勒出这个设计模式的代码组成结构。当我们一说o(n)的时候，也可以知道这段代码是如何组织的。

          还有很多常见的时间复杂度，比如o(1),o(n) o(logn) o(nlogn),o(n2)。下面说说我觉得最难分析的o(logn)这个时间复杂度把。

  int GetSum(int n)
  {
            var i = 1;
            while (i<=n)
            {
                i = i*2;
            }
            return i;
  }

        上面这个例子，一步步来分析，i=2,I=4,i=8,i=16,一直到i<=n。  那这个代码执行了多次呢。就是2的x次方小于等于n。 现在要求这个x是多少呢，那就用到我们的对数了x=log2为底，n为真数的对数了。

     int GetSum(int n)
        {
            var i = 1;
            while (i<=n)
            {
                i = i*3;
            }
            return i;
        }

        这个例子也是和上面是一样的，它是Log3为底,n为真数的对数。

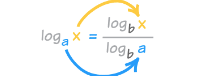
        我们知道对数是可以相互转化的了 。对数都是可以相互转化的，我们同时把他们转化为以十为底的对数，然后去掉常量，就得到了o(logn)。然后o(nlogn)就是n个o(logn)相乘。