树的基础知识和遍历

　　树的基本知识

　　　　树的基本结构，如下图所示：

           

　　　　二叉树：

　　　　每个节点最多只有两个子节点的树，叫做二叉。

　　　　满二叉树：如下图所示

　　      

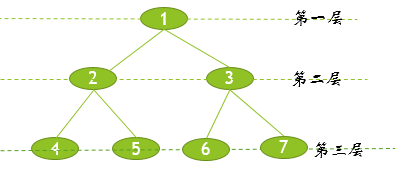
　　　　完全二叉树：

　　　　

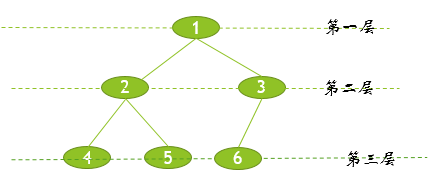
　　　　这两个有啥用呢，他们有规律，要记住他们的规律即可，啥规律后面用到再说。

　　二叉树的遍历

　　　　前序遍历：　

• 先出当前节点（root)，
• 如果左子节点不为空，则递归前序遍历。
• 如果右子节点不为空，则递归前序遍历。

　　　　中序遍历：

• 如果当前节点的左子节点不为空，则递归中序遍历
• 输出当前节点
• 如果当前节点的右子节点不为空的，则递归中序遍历

　　　　后序遍历：

• 如果当前节点的左子节点不为空，则递归后序遍历
• 如果当前节点的右子节点不为空的，则递归后序遍历
• 输出当前节点。

　　　　他们几种遍历方式的区别在于，啥时候输出跟节点。

　　接下来我们就思考如何用代码实现这遍历呢？

　　首先我们先要构建一颗树。

　　　　树的结构如下：

　　　　

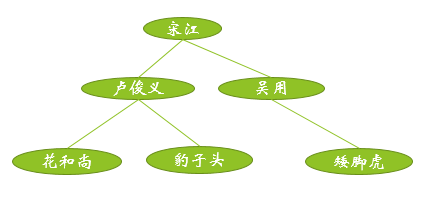
　　　　树的节点类，如下： 

　　　　有名字，编号（按顺序给他们安排上1-6），还有左节点，右节点。

public class HeroNode {

    private  int no;
    private String nickName;
    private String heroName;
    private HeroNode left;
    private HeroNode right;

    public HeroNode(int no,String nickName,String heroName){
        this.no=no;
        this.nickName=nickName;
        this.heroName=heroName;
    }

    @Override
    public String toString() {
        final StringBuilder sb = new StringBuilder("HeroNode{");
        sb.append("no=").append(no);
        sb.append(", nickName='").append(nickName).append('\'');
        sb.append(", heroName='").append(heroName).append('\'');
        sb.append('}');
        return sb.toString();
    }

    public HeroNode getLeft() {
        return left;
    }

    public HeroNode setLeft(HeroNode left) {
        this.left = left;
        return this;
    }

    public HeroNode getRight() {
        return right;
    }

    public HeroNode setRight(HeroNode right) {
        this.right = right;
        return this;
    }

    //前序
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }

    //中序
    public void infixOrder(){
        if(this.left!=null){
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right!=null){
             this.right.infixOrder();
        }
    }

　　 //后序
    public void postOrder(){
        if(this.left!=null){
            this.left.postOrder();
        }
        if(this.right!=null){
            this.right.postOrder();
        }
        System.out.println(this);
    }

}

　　接下来有了节点之后，定义一颗二叉树

public class BinayTree {

    private HeroNode root;

    public void setRoot(HeroNode root) {
        this.root = root;
    }

    public void preOrder(){
        if(this.root!=null) {
            this.root.preOrder();
        }else{
            System.out.println("没有数据，不用遍历");
        }
    }


    public  void infixOrder(){
        if(this.root!=null){
            this.root.infixOrder();
        }else{
            System.out.println("没有数据，不用遍历");
        }
    }

    public void postOrder(){
        if(this.root!=null){
            this.root.postOrder();
        }else{
            System.out.println("没有数据，不用遍历");
        }
    }


}

　　这个定义的过程中，我们把前序遍历，中序遍历，后序遍历的代码都给安排上了。

　　现在采用的是最简单的方法，递归实现的。

　　测试代码：

    public static void main(String[] args) {
       HeroNode node1=new HeroNode(1,"及时雨","宋江");
       HeroNode node2=new HeroNode(2,"玉麒麟","卢俊义");
       HeroNode node3=new HeroNode(3,"智多星","吴用");
       HeroNode node4=new HeroNode(4,"花和尚","鲁智深");
       HeroNode node5=new HeroNode(5,"豹子头","林冲");
       HeroNode node6=new HeroNode(6,"矮脚虎","王英");

       BinayTree binayTree=new BinayTree();

       node1.setLeft(node2);
       node1.setRight(node3);

       node2.setLeft(node5);
       node2.setRight(node4);

       node3.setRight(node6);

       binayTree.setRoot(node1);
       System.out.println("前序遍历");
       binayTree.preOrder();
       System.out.println("中序遍历");
       binayTree.infixOrder();
       System.out.println("后序遍历");
       binayTree.postOrder();
       
    }