20189221 2018-2019-2 《密码与安全新技术专题》第二周作业

20189221 2018-2019-2 《密码与安全新技术专题》第二周作业

课程：《密码与安全新技术专题》

班级： 201892
学号：20189221
上课教师：谢四江
上课日期：2019年3月12日
必修/选修： 选修

1.本次讲座的学习总结

​ 量子密码技术是量子物理学和密码学相结合的一门新兴学科，它是利用量子物理学方法实现密码思想的一种新型密码体制。 量子密码技术是一种实现保密通信的新方法，它比较于经典密码的最大优势是具有可证明安全性和可检测性。单词量子本身的意思是指物质和能量的最小微粒的最基本的行为。量子密码术与传统的密码系统不同，它依赖于物理学作为安全模式的关键方面而不是数学。

量子相关知识——薛定谔的猫

​ 如图所示，小盒子装有放射性源，设其半衰期为一个小时，即一小时后有一半概率放射出一个粒子，根据量子力学叠加原理，一小时后空间将处于有一个粒子（记为|1⟩），和没粒子（记为|0⟩）的叠加态|ψ⟩=12√(|0⟩+|1⟩))。

​ 如果有粒子，盒子的机关会被打开，于是铁锤就会掉落下去，打破装有毒气的瓶子，此时毒气会将密封于笼子里的猫毒死，当然如果小盒子未放出粒子，那么这只猫仍然活着。那么，一个小时后，这只猫究竟是活的还是死的？按照量子态叠加原理推演下来，猫也应当处在一半概率是活，一半概率是死的叠加态上。

薛定谔认为这种现象不符合人的基本常识，故量子力学是谬论。

研究背景及意义

经典密码体制

对称密码体制的优缺点：

  • 优点：加密速度快，适合批量。
  • 缺点：
  1. 密钥是保密通信的关键，如何才能把密钥安全送到收信方是对称加密体制的突出问题。
  2. 没有签名，不适合网络邮件加密需要。
  3. N个合作者，就需要N个不同的密钥，使得密钥的分发复杂。
  4. 通信双方必须统一密钥。

非对称密码体制的优缺点：

  • 优点：
    1. 公钥加密技术与对称加密技术相比，其优势在于不需要共享通用的密钥。
    2. 公钥在传递和发布过程中即使被截获，由于没有与公钥相匹配的私钥，截获的公钥对入侵者没有太大意义。
    3. 密钥少便于管理，N个用户通信只需要N对密钥。
    4. 密钥分配简单，加密密钥分发给用户，而解密密钥由用户自己保留。
  • 缺点：加密算法太复杂，加密与解密的速度比较慢。

实际使用——混合密码体制
使用公钥密码体制进行会话密钥分发，使用对称密码体制进行通信

量子密码体制

量子密码体制使用：
主要用于党政机关，实际使用中仅负责密钥分发。

量子密码算法：
- shor算法：提出大数分解，能在多项式时间内分解大数。受影响最大的密码体制为RSA等大数公钥密码
- Grover算法：提出搜索无序数据库量子算法，快速搜索算法。使密钥搜索的时间复杂度在二次加速的基础上得到了进一步的提速。

量子密码特点：

  • 并行性

  • 不可克隆定理

  • 测不准原理

  • 对未知量子态的测量可能会改变量子态

BB84量子密钥分配协议

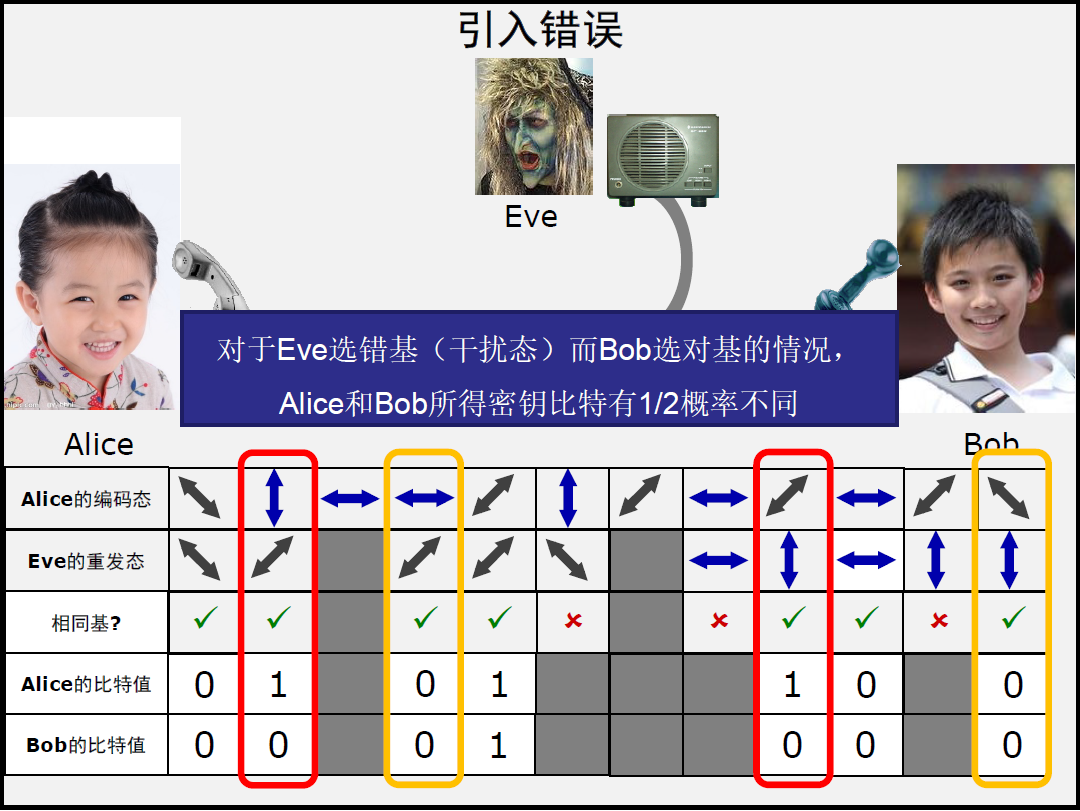
我们假设有一个监听者，Eve，尝试着窃听信息，他有一个与Bob相同的偏光器，需要选择对光子进行直线或对角线的过滤。然而，他面临着与Bob同样的问题，有一半的可能性他会选择错误的偏光器。Bob的优势在于他可以向Alice确认所用偏光器的类型。而Eve没有办法，有一半的可能性她选择了错误的检测器，错误地解释了光子信息来形成最后的键，致使其无用。而且，在量子密码术中还有另一个固有的安全级别，就是入侵检测。Alice和Bob将知道Eve是否在监听他们。Eve在光子线路上的事实将非常容易被发现，原因如下：让我们假设Alice采用右上/左下的方式传输编号为349的光子给Bob，但这时,Eve用了直线偏光器，仅能准确测定上下或左右型的光子。如果Bob用了线型偏光器，那么无所谓，因为他会从最后的键值中抛弃这个光子。但如果Bob用了对角型偏光器，问题就产生了，他可能进行正确的测量，根据Heisenberg不确定性理论，也可能错误的测量。Eve用错误的偏光器改变了光子的状态，即使Bob用正确的偏光器也可能出错。一旦发现了Eve的恶劣行为，他们一定采取上面的措施，获得一个由0和1组成的唯一的键序列，除非已经被窃取了，才会产生矛盾。这时他们会进一步采取行动来检查键值的有效性。

2.学习中遇到的问题及解决

  • 问题1：什么是量子隐形传态？

量子隐形传态主要是借助于量子纠缠态的概念来实现态的传递量子纠缠态是指 两体以上的量子态，对其中一体的改变必然会牵涉到另一体的相应改变，即不能分解为各自子系统内的张量积的形式,纠缠态的概念最早可上溯到1935 年提出的薛定谔猫的问题。例如，一个双光子纠缠态,对其中一个光子态进行某种方式的测量会导致其坍缩,另一个光子态尽管没受到直接的测量,也会发生相应的关联坍缩。

3.量子密码最新研究现状

  • 海森堡不确定性原则：这个原则说如果你衡量一件事，就不能准确地测量另一件事。例如，如果您将此原则应用于人类，则可以测量一个人的身高，但您无法衡量他的体重。关于这个原则唯一奇怪的是它只有在你尝试测量某些东西时才变为现实。该原理适用于光子。光子具有波状结构，并且在某个方向上偏振或倾斜。在测量光子偏振时，所有后续测量都会受到我们为极化做出的测量选择的影响。该原则在防止攻击者在量子密码学中的努力方面起着至关重要的作用[1]。
  • 光子偏振原理：这个原理指的是，由于无克隆原理，窃听者无法复制独特的“量子比特”（量子比特）即未知量子态。如果尝试测量任何属性，它将干扰其他信息。
  • 量子密钥分配（QKD）：经典密码学中存在一些流，同时分配密钥，这些流量在量子密码学中被量子密钥分发方法所克服。QKD用于生成使用两个信道在双方之间共享的秘密密钥。QKD使用两个频道。首先，量子信道用于传输单光子透明路径，它可以由光纤或空间制成。第二个是用于传输编码数据的经典频道，它可以是电话或互联网线路。[2] - [3]。
  • QKD基于以下协议。BB84协议：1984年，Charles H. Bennett和Gilles Brassard开发了第一个称为“BB84”的密钥分发协议。它基于海森堡不确定性原理[4]。

通信和消息传递协议的后量子安全：成就，挑战和新视角

广泛使用的通信和消息传递协议（例如，TLS 1.3和信号）对于具有量子计算机的对手是不安全的。Julia Bobrysheva和Sergey Zapechnikov预计，在近10 - 15年内，后量子安全将成为新一代加密协议的强制性要求。基于代码，格子，带有错误的环学习和椭圆曲线同构等中的难题，对用于密钥交换，加密和消息认证的现有后量子安全加密工具的分析揭示了它们的优点和缺点。特别是，我们得出结论，通信和消息传递协议的主要威胁只是当前使用的Diffie-Hellman密钥交换协议的预量子安全性。

有很多加密算法被认为可以通过量子计算机抵抗攻击：

  • 基于代数编码理论（基于代码）的密码学，其中一个例子是McElice加密代码方案（McEliece）;
  • 基于格的密码术（基于格的），其示例是NTRUEncrypt（N度TRUncated多项式环）;
  • 基于Merkle哈希树的密码学;
  • 基于有限域上多维多项式方程解的多元密码学。

面向部署光网络中CV量子密钥分配的集成

Fotini Karinou和Hans H. Brunner研究了在现有光学基础设施和波分复用（WDM）网络中集成Fotini Karinou和Hans H. Brunner开发的连续变量（CV）量子密钥分配（QKD）系统的进展。首先，Fotini Karinou和Hans H. Brunner研究了CV-QKD系统对自发拉曼散射（SRS）噪声的容忍度，后者是QKD的WDM共存环境中最主要的损伤。特别地，Fotini Karinou和Hans H. Brunner通过实验研究了WDM 10×10 Gb / s ON-OFF键控信号对QKD信道中的感应SRS噪声的影响。针对不同的传输场景，即针对WDM信号的各种光学发射功率，以及针对20,40,60和80km的不同传输链路，评估自发SRS噪声影响。根据实验数据和测量系统的参数，Fotini Karinou和Hans H. Brunner估计了拟议的CV-QKD系统的关键速率和覆盖能力。该方案支持20千米以上90 kbit / s的密钥速率，适用于复用2 mW光功率的理想QKD系统。更进一步，Fotini Karinou和Hans H. Brunner首次证明了使用上述CV-QKD系统来加密超过20公里的可部署光传输网络传统设备上的10GE客户端服务。Fotini Karinou和Hans H. Brunner的结果证明了Fotini Karinou和Hans H. Brunner提出的方案与现有WDM光网络中的传统电信设备的集成的可行性。Fotini
Karinou和Hans H. Brunner首次演示了上述CV-QKD系统的使用，以通过可部署的超过20公里的光传输网络传统设备加密10GE客户端服务。Fotini Karinou和Hans H. Brunner的结果证明了Fotini Karinou和Hans H. Brunner提出的方案与现有WDM光网络中的传统电信设备的集成的可行性。Fotini
Karinou和Hans H. Brunner首次演示了上述CV-QKD系统的使用，以通过可部署的超过20公里的光传输网络传统设备加密10GE客户端服务。Fotini Karinou和Hans H. Brunner的结果证明了Fotini Karinou和Hans H. Brunner提出的方案与现有WDM光网络中的传统电信设备的集成的可行性。

利用误差抑制编码实现单光子量子点的传输

Wei-Chao Gao和Si-Chen Mi通过实验证明了使用错误拒绝编码的忠实单光子量子比特传输，既不依赖辅助光子也不利用纠缠光子资源。使用非平衡偏振干涉仪，极化量子位被转换到时间段自由度上的状态。另外，可以以高保真度实现单光子量子态的确定性传输。时间仓编码量子比特对集体噪声的免疫性为量子信息科学中的实际量子误差校正和误差抑制铺平了道路。

用于超奇异同形Diffie-Hellman的优化模乘

Weiqiang Liu 和 Jian Ni ， Zhe Liu认为后量子加密（PQC）是指基于硬问题的加密方案，这些硬问题被认为能抵抗来自量子计算机的攻击。超奇异同构Diffie-Hellman（SIDH）密钥交换协议在已经提出的各种后量子密码系统之间显示出有希望的安全性。在本文中，我们提出了两种有效的模块化乘法算法，它们具有特殊素数，可用于SIDH密钥交换协议。还提出了两种提出的算法的硬件架构。提供硬件实现并与原始模块化乘法算法进行比较。结果表明，拟议的有限域乘数超过6。比硬件中的原始乘法器快79倍。此外，使用建议的FFM2硬件的SIDH硬件/软件协同设计实现比最佳SIDH软件实现快31％以上

从基于均衡的商业智能到信息保守的量子模糊密码学 - 双极模糊集到量子智能机械的细胞转换

张文然基于均衡商业智能（EBBI）和信息保守量子模糊密码学（ICQFC）的公理化公式，提出了双极模糊集到量子智能（QI）机制的细胞转换。事实证明，任何有源双极认知图都可以归一化为双极量子模糊认知图 - 信息保守双极量子模糊逻辑门的逻辑等价物，用于基于平衡的量子细胞再平衡。这种再平衡导致EBBI和ICQFC - 意外的协同作用的意外组合。示出了一种EBBI算法和两种ICQFC算法的适用性。ICQFC的信息理论安全性和可扩展性被证明是后量子密码学的计算智能测试平台。有人认为，虽然量子力学的不合逻辑方面阻止量子计算作为一种分析范式，但EBBI和ICQFC构成了双极模糊集到高精度QI机制的细胞转换 - 一种基于均衡的分析范式，用于普遍存在的量子建模和量子数字兼容计算。起草了QI架构。用ICQFC对EBBI说明了QI传输协议。因此，QI以其普遍存在的，分析性的，可转移的和量子数字兼容的特性而着称。据称，QI作为最通用的智力类型，通过数学，哲学和科学的区别来支持人工和生物智能。

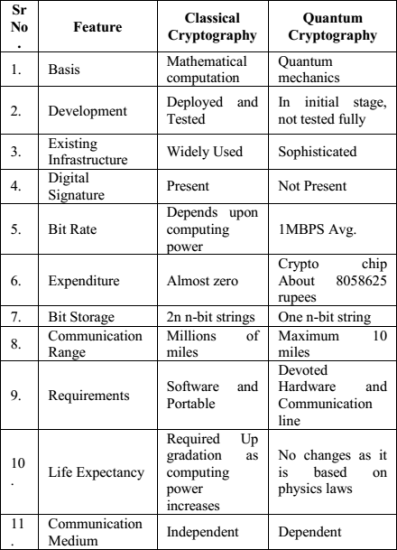
用于图像加密和解密的经典和量子密码学

在经典密码学中对“比特”起作用，即信息用“0”和“1”表示。而Quantum Cryptography适用于Quantum Bits，也称为“Qubits”。Qubit是双态机械系统，例如光子的极化。我们可以说量子比特可以是“0”和“1”的叠加，但这里有两种状态垂直偏振和水平偏振。在经典密码学中，Bits必须是“0”或“1”，但根据量子计算的基本属性，量子力学允许量子比特同时处于两个状态的叠加，这就是为什么它们不能被复制的原因

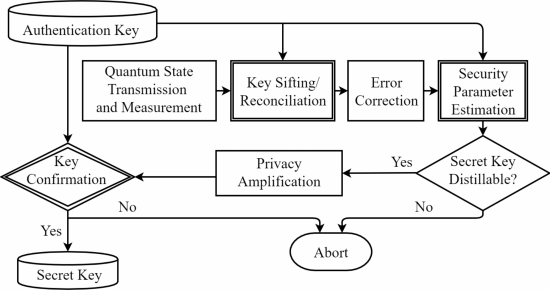
量子密钥分配（QKD）协议：一项调查

量子密钥分发（QKD）是一种新的安全技术，它依赖于量子力学的规律来共享密钥并提供无条件的安全性。通过使用量子力学定律，QKD具有不属于传统密码技术的新能力，即检测窃听者存在的能力。所有窃听者活动都可以被检测为错误。即使拥有无限的计算能力，QKD系统提供的安全性已被证明对攻击性攻击是强大的。QKD的第一个协议是由Bennett和Brassard在1984年提出的，也是1989年部署的QKD的首次成功实施。除此之外，还有一些很成功的QKD网络实施项目，如DARPA Quantum Network ，维也纳的SECOQC QKD网络在东京的QKD网络。

参考资料

posted @ 2019-03-21 19:29  古厉  阅读(645)  评论(1)  编辑  收藏  举报