35排序算法之合并排序

排序算法之合并排序

 

一、递归的合并排序

 

思想：合并排序（merge sort）又称归并排序，要点是反复将两个长度较短的有序段，合并成一个有序段，直到数组中只含一个有序段。

 

递归的合并排序算法：

   void  merge_sort(s)

   {

         if(s的长度不大于1) return;

         把s分成长度相等的两段s1和s2;    //长度至多差1

  merge_sort(s1);  //将两段分别排成有序段

  merge_sort(s2);

  merge(s1,s2);      //将两个有序段合并成一个有序段

   }

 

 

 

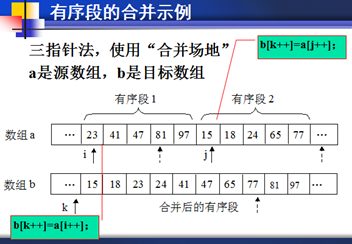
（1）有序段合并函数

void merge(int a[ ],int p,int q,int s,int t)

  { int i,j,k,b[n];   

1.   i=p,  j=s,  k=p-1;

2.   while((i<=q)&&(j<=t))

3.      if(a[i]<=a[j])  b[++k]=a[i++];

4.          else b[++k]=a[j++];

5.   while(i<=q) b[++k]=a[i++];

6.   while(j<=t) b[++k]=a[j++];

7.   for(i=p;i<=t;i++)a[i]=b[i];

  }

（2）主控函数

void  merge_sort(int a[ ],int i,int j)

    { int k;

8.    if(i<j)

9.      {  k=(i+j)/2; 

10.       merge_sort(a,i,k);  

11.       merge_sort(a,k+1,j); 

12.       merge(a,i,k,k+1,j); 

        }

}

主调语句： merge_sort(a,0,n-1);

 

        

 

二、非递归的合并排序

 

思想: 使用两个数组a和b，多遍合并完成排序.

第一遍，将数组a的长度为1的有序段，两两配对合并到数组b；

第二遍，将数组b的长度为2的有序段，两两配对合并到数组a；

第三遍，将数组a的长度为4的有序段，两两配对合并到数组b；

每合并一遍，有序段长度便增长一倍，经logn遍合并，排序完毕。

 

 

 

有序段的配对：

1）n=2k，每遍合并，恰好能将有序段两两配对，各有序段长度都等于“标准长度”。

2）n≠2k，某遍合并会余下“孤立段”，孤立段不参加本遍的合并，参加下一遍的合并。

3）孤立段会引起合并长度不等的一对有序段。

4）将上述三点归纳成， 一遍合并最后一对有序段情况，如下：

将一遍合并的标准长度t和最后两段长度t1和t2的四种可能：

① t1=t2=t          两段长 =标准长度t

② t1=t，t2<t    前段长=t，后段长<t

③ t1=t，t2=0    前段长=t，后段空

④ t1<t，t2=0    前段长<t，后段空

5）合并遍数必须是偶数，使最终结果在数组a中。

 

非递归的合并排序算法：

（1）主控函数merge_sort_2控制合并方向，确定本遍的有序段标准长度t的值

（2）函数scan将一遍合并的有序段两两配对

（3）函数merge_2 将配好对的有序段合并

 

（1）主控函数

void merge_sort_2(int a[ ],int n)

   { int b[n], t ; 

1.   t=1;      //有序段标准长度t初值为1

2.   while(t<n)

3.   {  scan(t,a,b,n);      //从 a 合并到 b

4.     scan(2t,b,a,n);    //从 b 合并到 a

5.     t=4t;          // t 扩大4倍

      }

   }

 

(2)合并函数

void mergex_2(int a[ ],int p,int q,int s,int t)

  { int i,j,k,b[n];   

1.   i=p,  j=s,  k=p-1;

2.   while((i<=q)&&(j<=t))

3.      if(a[i]<=a[j])  b[++k]=a[i++];

4.          else b[++k]=a[j++];

5.   while(i<=q) b[++k]=a[i++];

6.   while(j<=t) b[++k]=a[j++];

7.   for(i=p;i<=t;i++)a[i]=b[i];

  }

 

 

（3）控制一遍合并的扫描函数

void scan(int t,int a[ ],int b[ ],int n)

   { int  p,q,r;

6.   p=0;    

7.   while(p<n)

      {

8.      q=p+t-1;   r=q+t;

9.     if(q>n-1)  q=n-1;  //限制语句

10.     if(r>n-1)   r=n-1;

11.     merge_2(a,b,p,q,r);  // 合并两段

12.     p=r+1; 

      }

   }

 

非递归合并排序源代码：

#define N 15
void MergeArray(int *arr,int left,int mid,int right)
{//合并    
    int i=left,j=mid+1;  //可看成最后两组合并
    int    m=mid,n=right;
    int temp[N];//临时数组
    int k=0;
    while(i<=m&&j<=n)//把小的数放入临时数组
    {
        if(arr[i]<=arr[j])
        {
            temp[k]=arr[i];
            i++;
            k++;
        }
        else
        {
            temp[k]=arr[j];
            j++;
            k++;
        };
    };
    //可能某一组数值全是小的，没有存放在临时数组，补存
    while(i<=m)   
        temp[k++]=arr[i++];
    while(j<=n)
        temp[k++]=arr[j++];
    //把临时数组全部存放于原数组
    for(i=0;i<k;++i)
        arr[i+left]=temp[i];
};
//5归并排序（整体变部分，再合并）
void MergeSort(int *arr,int left,int right)
{//分离
    int mid=(left+right)/2;
    if(left<right)
    {
    MergeSort(arr,left,mid);
    MergeSort(arr,mid+1,right);
    MergeArray(arr,left,mid,right);
    };
};
int main()
{
    int arr[10]={3,5,8,2,4,13,9,1,16,7};
    MergeSort(arr,0,9);
    for(int i=0;i<10;++i)
        printf("%d ",arr[i]);
    getchar();
    return 0;
}