29排序算法之插入排序

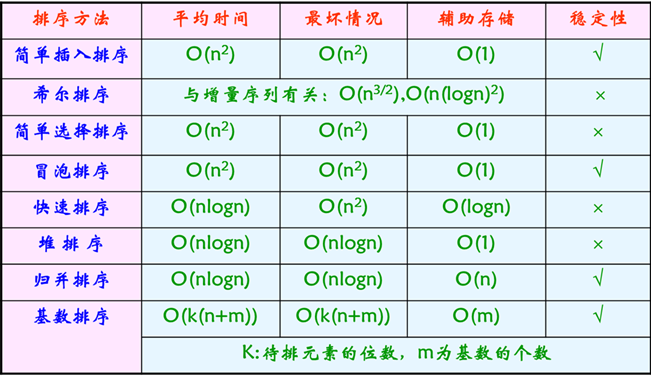
排序算法

 

排序的含义：排序（sorting），又称分类。是将无序序列变换成有序序列的一种运算。如果参加排序的数据结点含多个域，那么，排序往往是针对其中某个域而言的。

 

排序方法的分类:

按数据存储介质：内部排序和外部排序

按比较器个数：串行排序和并行排序

按主要操作：比较排序和基数排序

按辅助空间多少：原地排序和非原地排序

按稳定性：稳定排序和非稳定排序

按自然性：自然排序和非自然排序

 

排序算法之插入排序

原理：

基本操作：有序插入

在有序序列中插入一个元素，保持序列有序 ，起初，a[0]是长度为1的子序列，然后，逐一将a[1]至a[n-1]插到有序子序列中。

 

有序插入方法：

插入a[i]时，数组的前半段（a[0]至a[i-1]）已经有序，寻找有序位置j（j≤i），将a[i]插在a[j]的位置上。

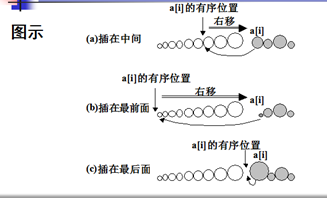
有三种可能：

（1）0<j<i，a[j-1]≤a[i]<a[j]

将元素a[j]至a[i-1]右移一位，再插入a[i]

（2）j=0，a[i]<a[0]，将a[i]插在最前面

       a[0]至a[i-1]全部右移一位

（3）j=i-1，a[i]≥a[i-1]，相当于插在尾部（不动）

 

 

寻找有序位置的方法:

用顺序查找

   直接插入排序（straight insertion sort）

 

用二分查找

二分插入排序（binary insertion sort）

 

直接插入排序算法之一:

void Sinsert_sort(int a[ ],int n)

   { int i,j,x;

1.  for(i=1;i<n; i++)

     {

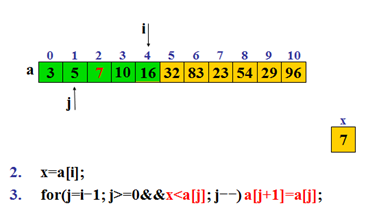
2.     x=a[i];     //空出a[i]的位置

3.     for(j=i-1; j>=0&&x<a[j]; j- -) a[j+1]=a[j];

4.     a[j+1]=x;  //将x 插在位置j

     }

 

 

直接插入排序算法之二（使用监督元）

void Sinsert_sort2(int a[ ],int n)

   { int i,j,x;

1.  a[0]=MIN;   //MIN是无穷小常数

2.  for(i=2;i<=n; i++)

3.   {  x=a[i]; 

4.     j=i-1;

5.     while(x<a[j]) a[j+1]=a[j- -];

6.     a[j+1]=x;

      }

   }

 

 

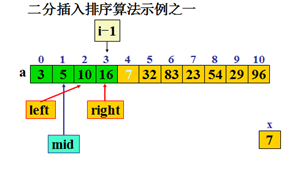
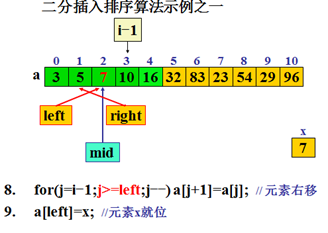
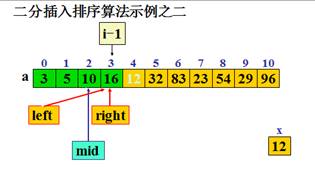
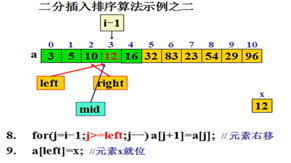
二分插入排序算法

void  Binsert_sort(int a[ ],int n)

   { int i,j,left,right,mid,x;

1.  for(i=1;i<n;i++)  //准备插入a[i]

2.   {   x=a[i];

3.       left=0;  right=i-1;

4.      while(left<=right)       

5.         { mid=(left+right)/2;

6.            if(x<a[mid])  right=mid-1;

7.               else   left=mid+1;       }

8.      for(j=i-1;j>=left;j- - ) a[j+1]=a[j]; 

9.      a[left]=x;  //元素a[i]就位      }

   }

 

 

 

算法的时间复杂性：

原始数据越接近有序，排序速度越快

最坏情况下（输入数据是逆有序的）

      TW(n)=O(n2)

平均情况下，耗时差不多是最坏情况的一半

    TE(n)=(n2)

为提高排序速度，要

     减少元素的比较次数

     减少元素的移动次数

 

插入排序源代码：
//3插入排序（选位置插数）
void InsertionSort(int *arr,int num)
{
    int i,j;
    int temp;   //存放要插入的数
    for(i=0;i<num;++i)
    {
        temp=arr[i];
        for(j=i;j>0&&arr[j-1]>temp;j--)
        {
            arr[j]=arr[j-1];
        };
        arr[j]=temp;
    };
};

int main()
{
    int arr[10]={3,5,8,2,4,13,9,1,16,7};
    InsertionSort(arr,10);for(int i=0;i<10;++i)
        printf("%d ",arr[i]);
    getchar();
    return 0;
}