27图的拓扑排序

拓扑排序

 

概念：将有向图G的顶点排成一个序列，使得，如果v到w有路，则v排在w之前（注意，并非v排在w之前，v到w就一定有路），拓扑排序所得的顶点序列是图的拓扑序列。

 

算法描述

步骤1）当图中存在入度为0顶点时，循环：

     ①任选一个入度为0的顶点v，输出v

     ②删去v，以及v射出的边

步骤2）循环终止时，如果已输出全部顶点，就得到一个拓扑序列，否则，表明图中有回路，不存在拓扑序列。

 

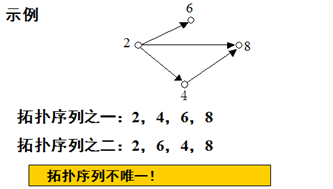
示例

 

 

 

 

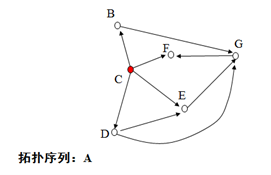
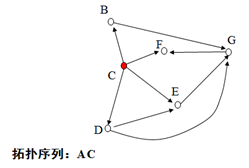
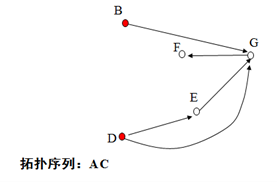
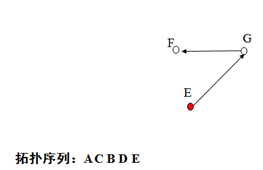
下面说说人话。。。。。。。。

拓扑排序步骤：

1.寻找出最开始的结点（因为是有向图，可以按箭头方向。无向图可任意）。

2.记住，记录一个点后，与这个点有关的所有边全部删除。如：记录点A后，那么A->B、A->C、A->D之间的边全部删除。

3.再一次寻找新的开始结点。。。重复以上步骤。。。。。。。。。。。。

 

 

 

实现方法

1.图用邻接表存储，表头结点含入度域indegree。

2.使用一个栈（零度表）存储入度为0的顶点。

3.当栈不空时循环，从零度表中删除（输出）顶点v，沿v的邻接表L[v]，将其邻接点w入度减1（若减到0，w加入零度表）。

4.使用一个计数器，统计输出的顶点总数。

 

拓扑排序算法（伪程序）

int topological_sort(***)          //“***”表示必要的参数

 {int v,w, count=0;  

   将栈stack置空;

   for(v=0;v<n;v++)    //n是顶点数

     if(L[v].indegree==0)将v推入栈stack中;

   while(栈stack不空)

    {  从栈stack中弹出一个顶点v;

      输出v;  count++;  

      p=L[v].firstarc;

      while(p!=NULL)

        { w=p->adjvex; //<v,w>是一条边

        L[w].indegree--;

        if(L[w].indegree==0)将w推入栈stack中;

        p=p->next;

          }

        }

  if(count<n) return 1;    //有回路

    else  return  0;     //没有回路

   }