26最短路径之Floyd算法

Floyd算法

思想：将n个顶点的图G“分成”很多子图

每对顶点vi和vj对应子图Gij（i=0，1，…，n-1和j=0，1，…，n-1）

每对顶点vi和vj都保留一条顶点限于子图Gij中的最短路径Pij（称为待定路径），其长度为Dij，不断地往子图Gij中增加“中间过渡点”（子图不断扩大），不断地将Pij优化（始终保持在Gij中是最短的），当图中所有n个顶点都作为中间过渡点加到子图Gij中时，子图Gij就变成了原图G，待定路径Pij也就变成最终所求的（在原图中的）vi到vj的最短路径。（注：i、j全部为字母下标）

 

步骤：

步骤1）开始时，每个子图Gij只含顶点vi和vj，vi到vj的当前最短路径就是边<vi，vj>本身

，若此边不存在，则认为其长度为无穷大。

步骤2）k从0到n-1，执行循环体：

           ①向子图Gij中加一个“中间点”vk

           ②如果Dik+Dkj＜Dij

            说明从vi到中间点vk，再由中间点vk到vj的路径

                  比vi到vj不经过中间点vk的路径短

            则修改待定路径Pij和其长度Dij，使

                Pij＝Pik接Pkj

                Dij＝Dik＋Dkj

 

示例

 

 

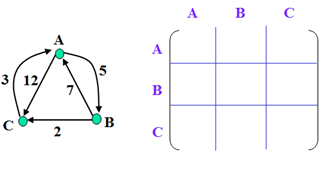
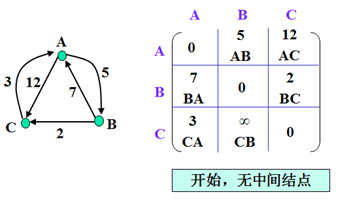
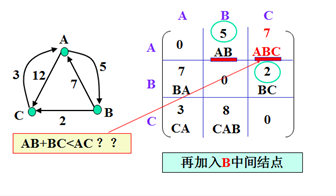
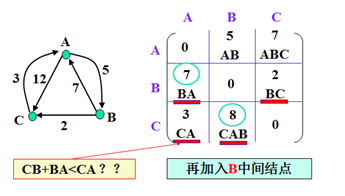
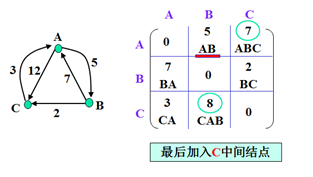
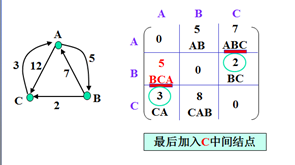
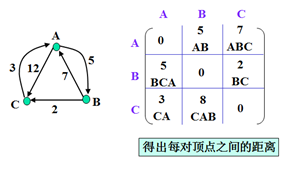
以上为官方示例。世俗观点还没出来。(本人还没完全弄懂，后续)。

 

Floyd算法（伪程序）

void Floyd(***)         //“***”表示必要的参数

  { int i,j,k;

     //初始化阶段

  for(i=0;i<n;i++)

    for(j=0; j<n;j++)

       { Dij=边<vi，vj>的长度;

        if(Dij不是无穷大) Pij=vi接vj; else  Pij=空；

           }

    //待定路径逐步优化阶段

    for(k=0; k<n;k++)      //加中间点vk

      for(i=0;i<n;i++)

        for(j=0;j<n;j++)

          if(Dij>Dik+Dkj)

            {  Dij=Dik+Dkj;

              Pij=Pik接Pkj；

              }

  }