21图结构的基本概念
图结构的基本概念
图的定义:用于描述多对多的网状关系。
由用于表示事物的顶点(vertex)集合V,以及表示事物之间关系的边(edge)集合E构成
记作G=(V,E)
顶点数目n>0,边数目m≥0
V:非空有穷顶点(vertex)集
E :V上的顶点对所构成的边(edge)集
边的概念:
1.边---有向边--------带有方向的边。
顶点v和w之间的有向边表示成<v,w>
v:边的尾(tail); w:边的头(head)
边是由v射入w的;
w是与v相邻(adjacent)的顶点(w是v的邻接点),有向边也称弧(arc)。
注意:<v,w>与 <w,v>是不同的边。
有向边用带箭头的线条表示,箭头指向边的头

2.边----无向边-------不带方向的边
顶点v和w之间的无向边表示成(v,w)。
边是关联于v和w。而v与w互为邻接点。
注意:(v,w)与(w,v)表示同一条边。
无向边用不带箭头的线条表示。

另外:
边表示顶点间的某种关系:
无向边:对称关系(如同志关系)
有向边:非对称关系(如领导和被领导关系)
单行道:有向边;双行道:无向边
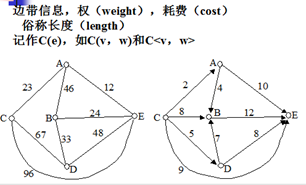
3.边----加权边--------边附带一个实数作为权
边的权可以表示边的长度、沿着边旅行所需的费用或时间、工程(输电线路、通信线路、高速公路等)造价等(这里只研究非负权)。
权又统称为耗费(cost),俗称长度(length),但不一定满足三角不等式(两边之和大于第三边)。
注意:画图形时,权标在边的旁边。

示例:
图的图形表示法(必须遵循以下五点)
1.圆圈表示顶点,线段表示边
2.无向边(v,w)不带箭头
3.有向边<v,w>的线段带箭头,箭头指向顶点w
4.加权边的权标注在边的旁边
5.顶点名称写在圆圈内,或标注在圆圈旁边
比如:顶点名称用大写字母A,B,C,D…,
或“北京”、“南京”、“上海”等
顶点变量名用小写字母 v,w,s,…
或v0,v1,…
图的种类
1.有向图:边都有向。
2.无向图:边都无向。
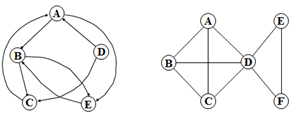
4.混和图:有些边有向,有些边无向(可化为有向图)。
5.简单图:无重复边,无到自身的边(形如<v,v>的边)。
注意点:
无向简单图:两个点之间最多只有一条边 ,而且没有自环(自回路)。
有向简单图:无自环,无重复边(允许<v,w>和<w,v>同时存在)。
6. 多重图:无上述限制。
注意点:
无向多重图:图中有重复边;有到自身的边(环)。
有向多重图: 图中允许有两条<v,w>、<v,w>同时存在;也允许环存在。
7. 加权图:边均带权。
边权图称网(network),非加权图也称0/1图。
边的权通常不满足三角不等式 ;“拓扑”结构图。
重点
图的相关术语:
1.有向图的顶点度:
v的出度(out-degree):v射出的边数(以v为尾)
v的入度(in-degree):射入v的边数(以v为头)
v的度(degree):v的出度与入度之和

2.无向图的顶点度:
v的度(degree):与v关联的边数。
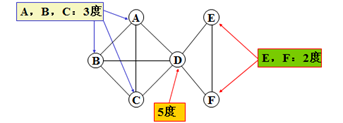
注意:
所有顶点的入度之和=出度之和=边数(有向图)
所有顶点的度数之和=边数的两倍(无向图)
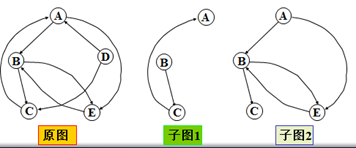
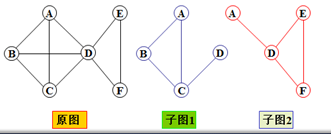
3.子图
子图就是原图的一部分,由原图中部分顶点,以及这些顶点之间的一部分边组成的图。但必须与原图的那一部分一模一样。
4. 路径和回路
路径(path) :首尾相接的边序列。
回路径(cycle):起点与终点重合的路径
简单路径:边不重复;
基本路径:中间无重复顶点。
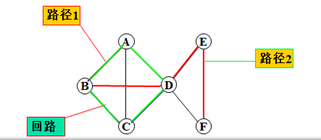
路径 (path)(通路):首尾相接的边序列。
起点和终点:路径上的两个端点。
路径长度(length):路径上的边数。
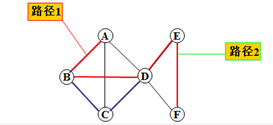
简单路径:顶点不重复
回路(cycle)(圈):起点和终点相重合的简单路径
加权图中的加权路径耗费=路径上边耗费之和
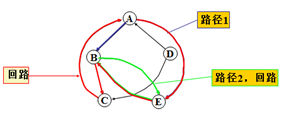
5.无向图的连通性
v与w连通(connected):顶点v到w有路径,也称v可到达w。
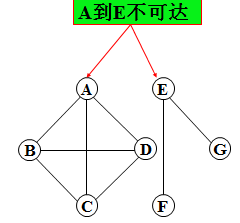
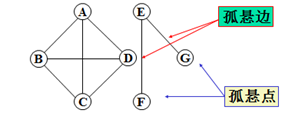
孤立点:与任何点都不连通
孤悬边:删除边(v,w)后,v或w就变成孤立点。
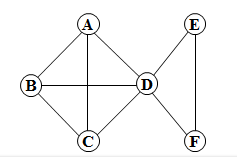
连通图(connected graph):任何两顶点都连通。
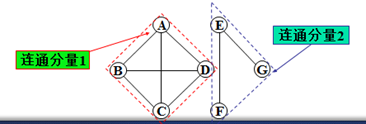
连通分量(connected component):极大连通子图,连通图只含一个连通分量。(极大指的是在满足连通的条件下,尽可能多的含有图中的顶点以及这些顶点之间的边。)
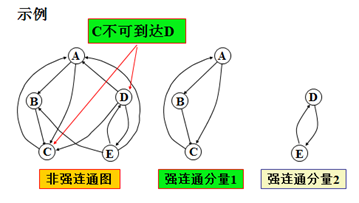
6.有向图的连通性
v与w连通(connected):v到顶点w路径,也称v可到达w。
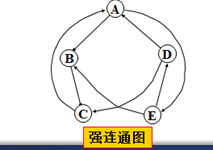
强连通图(strongly connected graph):任何两点v和w均相互连通。
强连通分量(strongly connected components,或strong components):
极大强连通子图,强连通图只含一个强连通分量。
注意:
v和w单向连通:v到w有路径(v可达w)。
v和w互连通的(双向连通):v到w,和w到v都有路径。
强连通的(strong connected):G中任何两个顶点都互连通。
强连通分量(connected component):G'=(V',E')是G=(V,E)的由V'导出的强连通子图,而且V-V'中的任何顶点都不与V'中任何顶点双向连通。
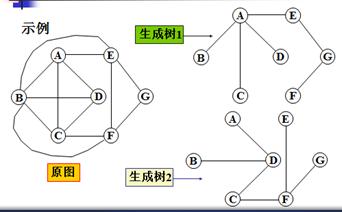
无向连通图的生成树(spanning tree):
是图的一种连通子图,它含有图的全部n个顶点,但只含有足以使图保持连通的n-1条边。
生成树也称支撑树,生成树不唯一。
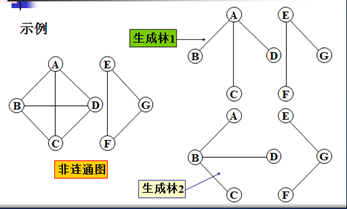
生成森林(spanning forest):无向非连通图每个连通分量有一棵生成树,构成图的生成森林。
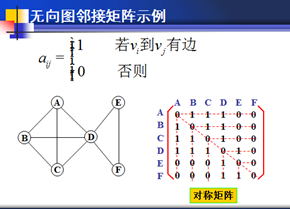
图如何以矩阵形式存储?--------邻接矩阵
顶点表示事物,边表示事物间的关系,对应的关系矩阵。
顶点对应矩阵的行列号,边对应矩阵元素值。
0/1图对应的邻接矩阵是0/1矩阵:顶点v和w之间有边,矩阵第v行第w列元素值为1;否则为0。
加权图对应的邻接矩阵(也称耗费矩阵)是实数矩阵:对角线元素值均为0;顶点v和w之间有边,矩阵第v行第w列的元素值为该边的长度 ;否则为∞。
注意点:无向图的邻接矩阵是对称矩阵。
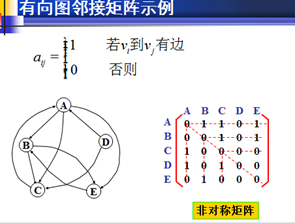
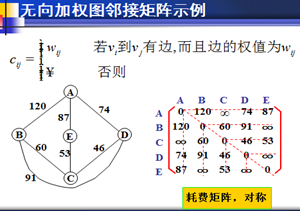
邻接矩阵的顺序存储:
因为邻接矩阵是一个n×n的方阵,所以可采用一般矩阵的存储方式。
(1)二维数组存储
最直观的存储方式用二维数组(比如a[n][n])存储称为图的邻接数组(adjacency array)。
优点:可直接从v行w列读出边<v,w>信息
缺点:存储量较大
适用情况:边数相对较多的有向图
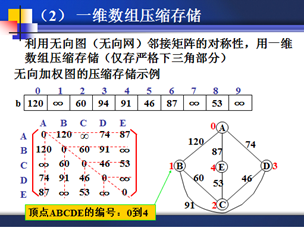

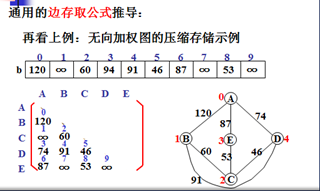
存储效率分析:
邻接数组存储法(无论是否压缩)是边集的一种顺序存储方式。
优点:简单,极易在图中查找、插入、删除一条边
缺点:存储n个顶点的图,要占用O(n2)个存储单元
(无论图中实际含多少条边)
图的读入、存储空间的初始化等需要花费O(n2)个单位时间。
对于边数m<<n2时的稀疏图是不经济的。
存储稀疏图最好采用邻接表法。
邻接表
概念:顶点v的所有邻接点组成的表,称为v的邻接表L[v],各顶点邻接表总称为图的邻接表 (adjacency lists),邻接表采用链式存储(即邻接链表),L[v]中每个结点对应图中一条边,称为边结点。
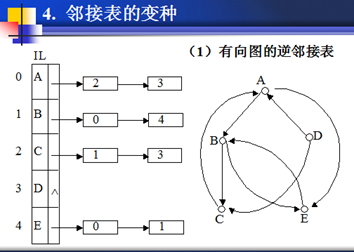
对有向图,若存在边<v,w>,则w处于L[v]中。
对无向图,若存在边(v,w),则w处于L[v]中,同时v也 处于L[w]中。
n个顶点的邻接链表构成一个链表组,使用一个表头指针数组将n个链表结合在一起。
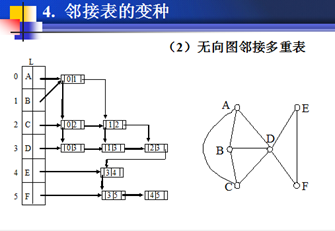
邻接表通常设计成单向链表形式,根据需要,也可设计成双向的、或其他形式的链表。
(2)边结点结构
不同的图采用不同的边结点结构
下面分别介绍加权图和0/1图的边结点结构定义形式
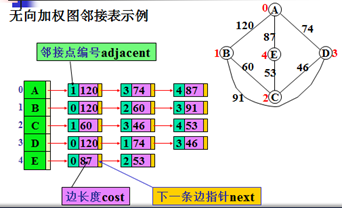
(1)加权图的边结点类型定义:
含有邻接点名称(编号)域、边的长度(耗费)域和指向下一个边结点的指针域。

边结点的类型定义:
typedef struct edge_node
{ int adjacent; // 邻接点名称域
cost_type cost; // 边的耗费域
struct edge_node *next; //指各下一个边结点
} edge_node, *Eptr;
(2)0/1图的边结点类型定义:
含有邻接点名称(编号)域和指向下一个边结点的指针域。

边结点的类型定义:
typedef struct edge_node
{ int adjacent; // 邻接点名称域
struct edge_node *next; //指各下一个边结点
} edge_node, *Eptr;
(3)邻接链表的表头结点(顶点结点)结构定义:
含有顶点名称域和指向邻接表首结点的指针域。必要时,可增加其他域。

顶点结点的类型定义:
typedef struct edge_node
{ Vname_type name ; //顶点名,用于由号查名
Eptr firstedge ; //邻接表的首指针
} hnode ;
表头结点组定义为:
hnode L[n]; //n为具体顶点数