19哈夫曼树

哈夫曼树

 

定义：给定n个正实数w1至wn，使权WPL(T)达最小值的树，称为哈夫曼树（最优二叉树）。（其中n表示该树中叶结点的数目，wk和lk(k=1,2,···,n)分别表示叶结点ik的权值和从树根到叶结点ik之间的路径长度。）

注意：哈夫曼树必是正则二叉树！

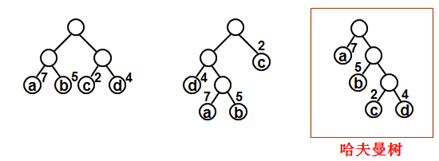
下面还要明白几个重要的概念：

1. 叶的路径长度：指从根结点到叶结点的路径上的边数。

 

2. 叶的加权路径长度：设二叉树T具有n片叶子，n个正实数w1至wn作为各叶的权，根到第i（1≤i≤n）片叶子的路径长度为l_i，那么，W_i*l_i称为该叶的加权路径长度。

 

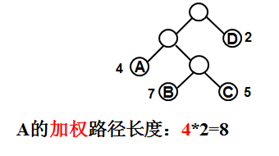
3. 二叉树T的权：n片叶子加权路径长度之和称为二叉树T的权WPL(T)。

 计算公式：

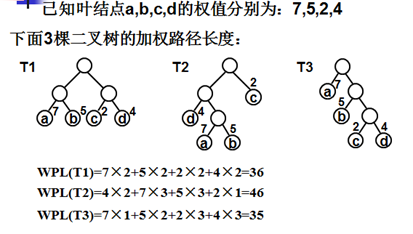
此时，要注意, 加权路径长度为最小的二叉树不是唯一。在构建哈夫曼树时，相同的数值，可能会出现不同的哈弗曼树，但是都是最小路径。

 

 

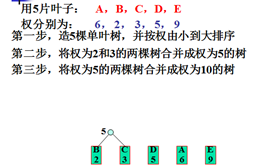
哈夫曼算法的描述：自底向上，逐步合并。

 

具体步骤:

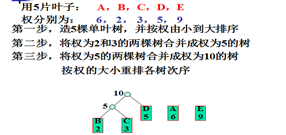
步骤1）构造n棵单叶结点的二叉树，构成初始森林。将权w1~wn依次赋给各叶。

步骤2）按下述步骤，反复将森林中的两棵树合并成一棵树，直到森林中只有一棵树，这棵树就是哈夫曼树。

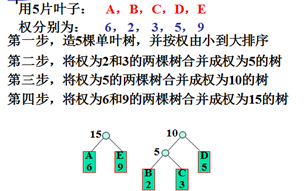
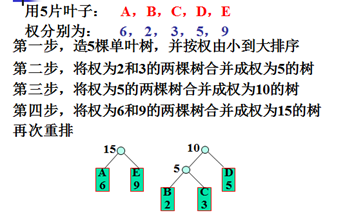
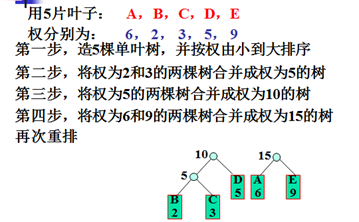
①在森林中找出根的权最小的两棵树：T1和T2。

②将T1，T2合并成一棵树T，使T1，T2分别作为T的左右子树，且使T之根的权等于T1，T2之根的权之和。

③把合并树T加入森林。

 

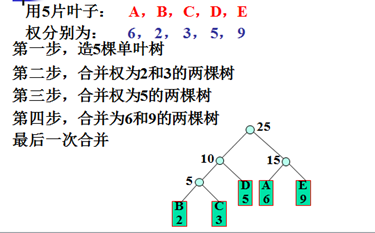
示例：

 

 

 

构造哈夫曼树的源代码：
（1）有关定义
#include  <stdio.h>
#define  n  XX    //XX为具体叶子数目
#define  MAX  YYY    //YYY代表无穷大值，用作监督元
#define  NULL  0        //空链域值
typedef  struct  Hfnode    //结点类型
{  int  data;            //权值域，假定为int类型
   struct  Hfnode  *Lson, *Rson, *next;  //儿子链域和森林链域
}  Hfnode,*Hfptr;

结点类型定义：
typedef  struct  Hfnode   //  结点类型
 {  
　　int  data;  //权值域，假定为int类型
   struct  Hfnode  *Lson, *Rson, *next; 
 } Hfnode,*Hfptr;
主控函数：
void  Hfmain( )  
 { 
　　 Hfptr Hroot,head; 
    head=inition( );  //调用初始化函数
    Hroot=creatHftree( );//调用造树函数
   ……  //其它处理
  }
初始化函数：
Hfptr  inition( )
  { 
int i; 
Hfptr h,p;
   h=p=new Hfnode;
   h->data=MAX;   //构造监督元结点 
   for(i=1;i<=n;i++)
     {  
　　　　p->next=new Hfnode; 
        p=p->next;  //p始终指向当前尾结点 
        p->Lson=p->Rson=NULL; //做叶结点
        scanf("%d",&p->data); //读入叶之权wi
      }
.   p->next=h;  //构成循环链
    return  h;
  }
构造哈夫曼树的函数：
Hfptr  creatHftree(Hfptr  head) 
  {
　　int i;
　　Hfptr  p,q,r,t1,t2;  
    for(i=1;i<n;i++) //进行n-1遍合并
　　{
　　　　r=new Hfnode; // 申请新根
      t1=head->next; // t1，t2指向两棵权最小的树根
      t2=t1->next;   
      r->data=t1->data+ t2->data; //权值相加
      r->Lson=t1; // t1，t2作新根r的左右儿子
      r->Rson=t2;
      head->next=t2->next;  //森林中删去t1，t2
      q=head; //准备进行有序插入
      p=head->next; //p是搜索指针，q是p的前趋
      while(1) //循环的为r寻找有序位置 
          {
　　　　　　　　if(p->data<r->data)
       　　　 { 
　　　　　　　　　　q=p;  
　　　　　　　　　　p=p->next; 
　　　　　　　　} //尚未找到时，继续循环
    　　　　    else
     　　　　   { 
　　　　　　　　　　 r->next=p; //找到后，插入r
     　　　　      q->next=r;
      　　　　     break;
      　　　　   }   
　　　　　　}
    } //终止语句1 的for循环
 　　  p=head->next; 
 　　 delete  head;  //删去监督元
 　　  return  (p);  //返回Huffmam树之根
   }  //构造完毕