16平衡树
平衡树,又称AVL树。(以前苏联学者Adelson-Velskii和Landis的名字命名)
定义:所有结点的平衡因子绝对值≤1的二叉树(高度h控制在结点数n的对数范围之内 h≤O(logn)的树都属于平衡树(balanced tree))。
平衡因子:右子树的高hR与v的左子树高hL之差hR-hL 。
AVL树各点的平衡因子:只能是0、1、-1。
性质:高度h≤1.45log2n (n是结点数)
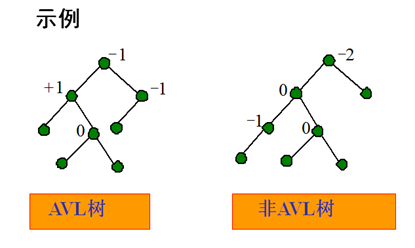
换句话说,以某一点为根结点,再以其右子树的高度减去其左子树的高度。其值只能是0,-1,1。
比如: 最顶端是根结点,其右边高度减左边高度,所以其根结点的平衡因子为0。
最顶端是根结点,其右边高度减左边高度,所以其根结点的平衡因子为0。
一、插入引起的旋转
(1)插入操作的大体步骤
步骤1) 像一般的检索树那样插入x(新叶)
步骤2)沿插入x的路线返回,修改x祖先的平衡因子
步骤3) 回溯中,一旦发现x的祖先p失衡
由p->bal=1 变成 p->bal=2
由p->bal=-1 变成 p->bal=-2
旋转以p为根的子树,使之平衡
(2)平衡因子变化情况分析
x插在p的左子树上,且使p的左子树高度增1
当返回路线沿左路到达p时 ,插入前 :
p->bal=0(hR=hL=h)
p->bal=1(hR=h,hL=h-1 )
p->bal=-1(hR=h,hL=h+1 )
(3)旋转方法
前提(左子树) :p->bal=-1 变为 p->bal=-2
1. LL单旋:p的左儿子作根
2. LR双旋:p的孙子作根
前提(右子树) :p->bal=+1 变为 p->bal=+2
1.RR单旋:p的右儿子作根
2.RL双旋:p的孙子作根
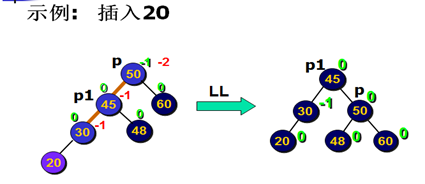
LL单旋
具体情况及方法:
情况:x插在p的左儿子p1的左子树上,使p1的左子树升高,继而引起p1点升高
插入x前,p1->bal=0;
插入x 使p1的左子树升高,p1->bal变为-1
现沿左路到达p1,又沿左路到达p。
旋转方法:
(1)使p1作为子树之根
(2) p作p1的右儿子;p1的右儿子作p的左儿子
旋转后:p子树高度没有增加,停止回溯

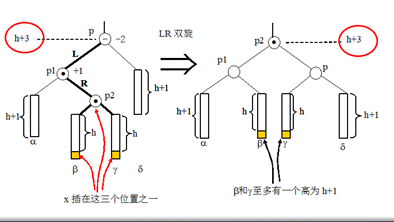
LR双旋
情况:x插在p的左儿子p1的右子树上,使p1的右子树升高,继而引起p1点升高
插入x前,p1->bal=0;
插入x 使p1的右子树升高,p1->bal变为1
现沿右路到达p1,又沿左路到达p
旋转方法:
(1)p2作为子树之根
(2)p1和p分别作p2的左右儿子
(3)p2的原左右儿子分别作p1的右儿子和p的左儿子
旋转后:p子树高度没有增加,停止回溯

结论:
1.插入一个结点,至多旋转一次
2.从右路返回到p的处理完全对称(旋转:RR单旋、RL双旋)
3.“左”都换成“右”,“右”都换成“左”
4.正号都换成负号,负号都换成正号
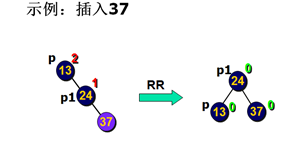
RR单旋
旋转方法:
(1)使p1作为子树之根
(2) p作p1的左儿子;p1的右儿子作p的左儿子
旋转后:p子树高度没有增加,停止回溯
RL双旋
旋转方法:
(1)p2作为子树之根
(2)p和p1分别作p2的左右儿子
(3)p2的原左右儿子分别作p1的右儿子和p的左儿子
旋转后:p子树高度没有增加,停止回溯
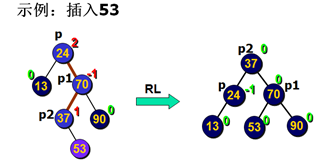
构造AVL树实例

步骤:
1.按照构造有序二叉树的方法(左小右大),构造有序二叉树。
2.按照上述方法,使用哪种旋转方法。可能要使用多种的结合,不局限于一种。
二、删除引起旋转
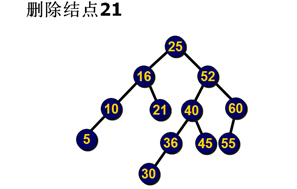
(1)删除结点x的大体步骤:
步骤1)用一般检索树的删除算法找到并删除结点x,x有两个儿子时,被删除的是x的中序前趋。
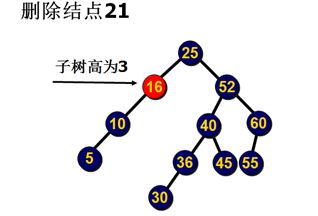
步骤2)沿根到被删除结点的路线之逆逐层向上回溯,检查该路线上各结点的平衡因子是否变化,如果变化,则及时修改。
步骤3)若发现某结点p的平衡因子,由p->bal=1变成p->bal=2,或由p->bal=-1变成p->bal=-2(失衡),则旋转以p为根的子树结构,恢复平衡。
如果旋转后子树高度还降低,要继续回溯。
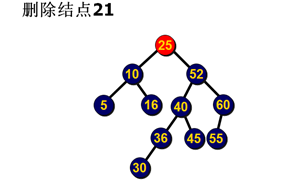
(2)平衡因子变化情况分析
在p的左子树上删除,使p的左子树高度降1。
删除前p的平衡因子(分三种情况)
p->bal=-1
p->bal=0
p->bal=+1
总结:
删除前p的平衡因子(分三种情况)
1.p->bal=-1
p->bal变为0,树高降低,回溯
2.p->bal=0
p->bal变为-1,树高不变,平衡
3.p->bal=+1
p->bal变为+2,旋转
(3)旋转方法
情况:在p的左子树上删除,使p的左子树高度降1
删除前,p->bal=+1;
删除后,p->bal变为+2
考虑:p的右儿子p1的平衡因子。
p1->bal=0
p1->bal=+1
p1->bal=-1
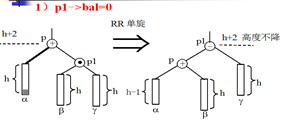
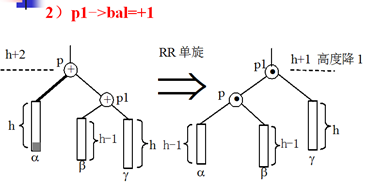
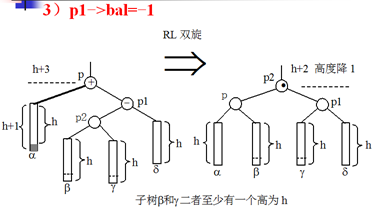
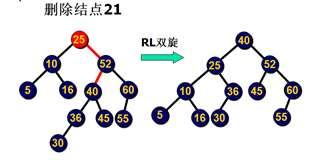
旋转方法(结论):
情况:在p的左子树上删除使p的左子树高度降1
删除前,p->bal=+1
删除后,p->bal变为+2
考虑:p的右儿子p1的平衡因子
p1->bal=0 RR单旋 平衡
p1->bal=+1 RR单旋 树高降低
p1->bal=-1 RL双旋 树高降低
旋转后:子树高度如果降低,继续回溯
删除示例:
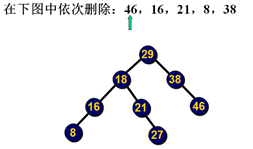
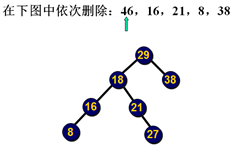

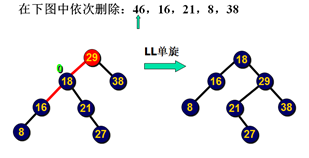
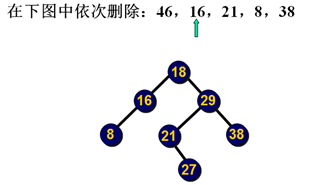
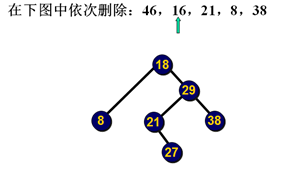

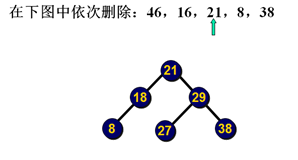
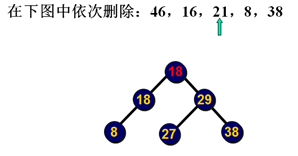

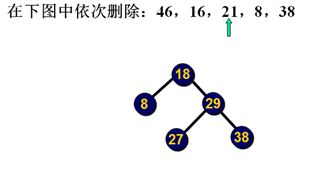

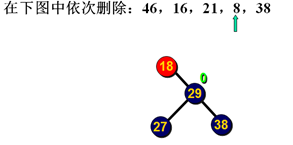

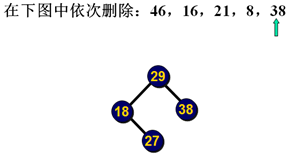
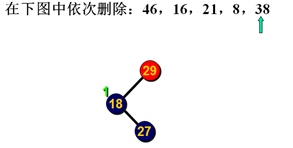
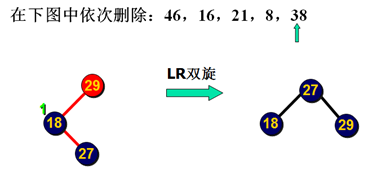
删除示例2