12二叉树的基本概念和性质
二叉树的基本概念和性质
二叉树的定义:二叉树(binary tree)也称二分树,是二元位置树。每一个结点的度至多为2。
每个结点最多有两个儿子(左儿子、右儿子)
结点的两棵子树叫做左子树和右子树
二叉树的基本性质:
1) 非空二叉树中,第i层(i≥1)上结点的个数
ni≤2i-1
2)高为k(k≥0)的二叉树中,结点总数mk满足:
mk≤2k-1
3) n个结点的二叉树的高h至少1+[log2n]
(即h≥1+[log2n]),其中,方括号表示“下取整”
满二叉树和完全二叉树:
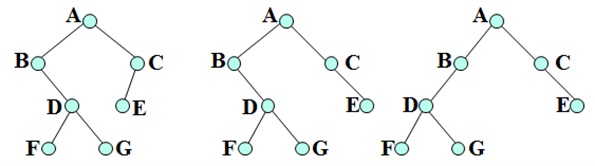
(1)满二叉树(full binary tree)也称丰满二叉树,高为k的二叉树,结点数达到最大值2k-1的二叉树。

(2)完全二叉树(complete binary tree),也称左满二叉树,或顺序二叉树,是由满二叉树的编号从1到n的前n个结点(这里n≤2k-1)构成的二叉树。
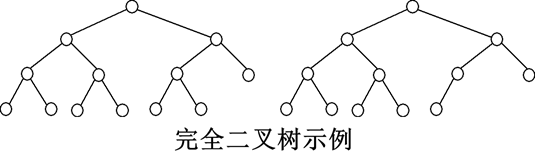
注意:
完全二叉树是满二叉树的一部分
满二叉树是完全二叉树的特例
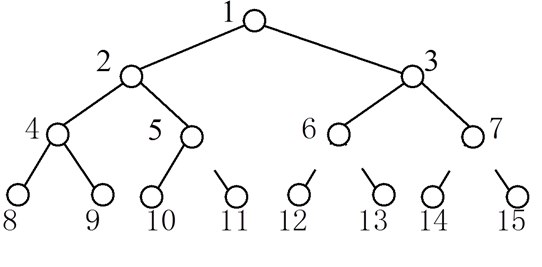
完全二叉树的性质:
1) n个结点的完全二叉树的高度k=1+[log2n]。
2) 编号为i(1≤i≤n)的结点父亲儿子的编号满足:
父结点的编号为:father(i)=[i/2]
(但i=1时,是根,无父亲)
左儿子编号为:Lson(i)=2i
(但2i>n时,是叶,无左儿子)
右儿子编号为: Rson(i)=2i+1
(但2i+1>n时,无右儿子)
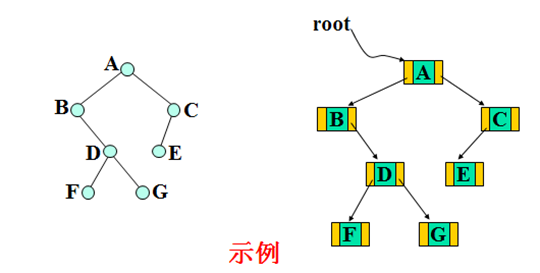
普通树与二叉树的转换
将普通树T转换成二叉树B的步骤如下:
步骤1)使T之根作为B之根
步骤2)对于所有已经转换过的结点f和尚未转换过的结点s,反复做下面两步:
步骤3)如果结点s在T中是结点f的第一个儿子,那么在B中让s作为f的左儿子
步骤4)如果结点s在T中是紧靠结点f的“下一个”兄弟,那么在B中让s作为f的右儿子.
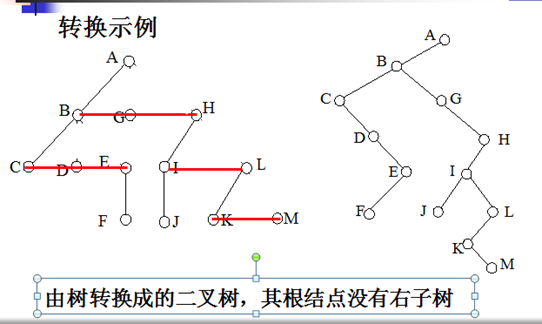
换句话说,在原普通树的前提下,就是将兄弟结点用一根线代替,变成第一个兄弟结点的子孙结点。
森林与二叉树的转换
转换步骤:
1)给森林增设一个虚拟根结点,使森林中各树的根都作为该虚拟根的儿子,把森林变成一棵普通树
2)按普通树转换成二叉树的方法将这棵树转换成二叉树
3)删去虚拟根结点,而以虚拟根的左儿子为根,就得到由森林转换的二叉树
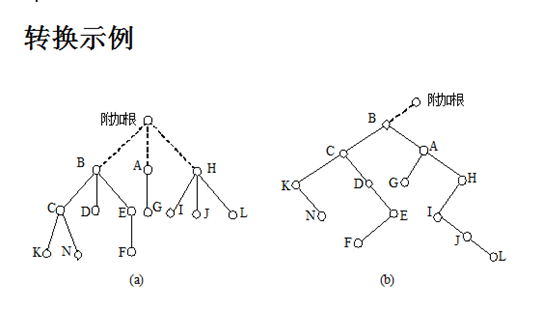
换句话说,森林无非就是多个根结点,那么将这几个根结点变成孩子结点,在其前驱加一个共同父亲结点,此时就是一颗普通树。就按普通树进行转换。
二叉树转换成森林(或普通树)
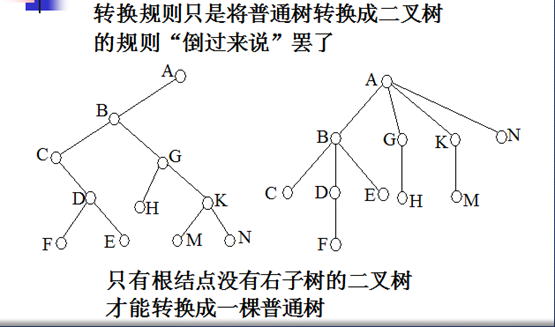
将二叉树B转换成普通树T的步骤如下:
步骤1)给二叉树B增设一个附加根R,原根作附加R的左儿子。
步骤2)使R作为转换后树T的根。
步骤3)对于所有已经转换过的结点f和尚未转换过的结点s,反复做下面两步。
步骤4)如果结点s在B中是结点f的左儿子,在T中s作为f的第一个儿子。
步骤5)如果结点s在B中是结点f的右儿子,在T中s作为f的兄弟,即作为f之父的另一个儿子,这个儿子紧靠在f的右侧。
步骤6)删去附加根R,得到最终的转换结果。
1.普通树的存储方法
(1)多重链接法
存储m元树用m重链表,结点结构的定义
typedef struct tnode
{ element_type data; //假定结点值域类型
struct tnode *son[m]; //指向各个儿子的链域
} tnode,*tptr; //定义结点类型和指针类型别名
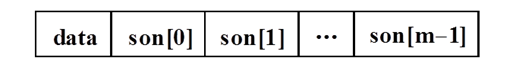
(2)左儿子右兄弟链接法
结点结构定义
typedef struct tnode
{ element_type data;
struct tnode *son,*sibling;
} tnode,*tptr;
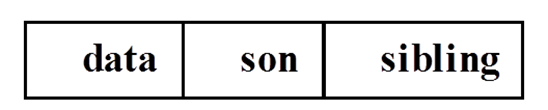
特点:
定位根,适合于“从上而下”的搜索,从儿子找父亲很困难,除非加指向父亲的链域(father)
(3)父亲链接法
条件:结点值(或编号)是0到n-1的整数
用数组tree[n]存储,tree[i].father存储结点i的父亲。
若结点j是根,则root=j,且tree[j].father= -1
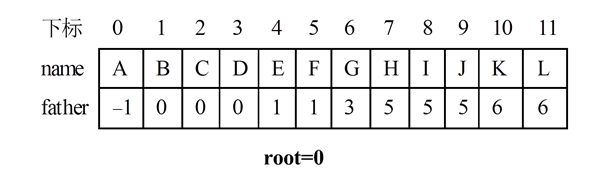
特点:
1.数组的下标是结点的编号(像静态链表)
2.容易由儿子找到父亲
3.无法从父亲找到儿子
4.必须能够将结点名(值)快速变换成编号
二叉树的存储方法
(1)完全二叉树的顺序存储
用数组a[n+1]存储完全二叉树的n个结点(a[0]不用),使编号为i的结点存放在a[i]中,
a[1]是根结点,a[2],a[3]是根的两个儿子……结点a[i]的父结点是a[i/2],其左右儿子是a[2*i]和a[2*i+1]。(如果它的父亲、左右儿子存在的话)
特点:节省链域,查找父亲、儿子特别快。
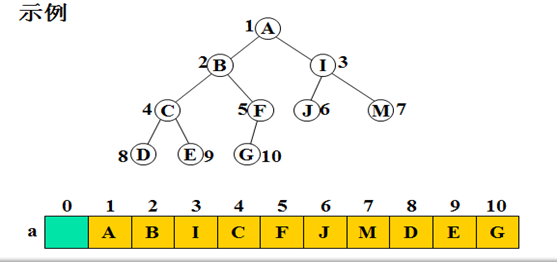
(2)普通二叉树的双链存储
结点含有值域和指向左儿子和右儿子的链域
typedef int element_type; //假定结点类型是int
typedef struct Bnode //定义二叉树结点类型Bnode
{
element_type data; //data域
struct Bnode *Lson, *Rson; //指向左右儿子的链域
} Bnode, *Bptr; // 定义结点类型名,和指针类型名
Bptr root,p; // 定义指针变量

特点:根定位(使用根指针),便于从上向下搜索。