11树结构的基本概念

书结构的基本概念

 

树的定义：用于描述层次关系、分枝关系、嵌套关系的基本数据结构。（首结点没有前驱，其他结点有且只有一个前驱，或有多个后继。）

 

树（tree）是n（n≥0）个结点的集合

若n=0，是一棵空树（null tree）

   n=1，是一棵单结点树

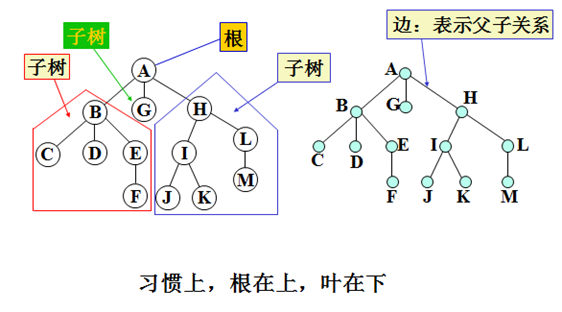
   n>1，其中一个结点是树的根结点，简称根（root），其余结点被划分成若干个子集，每个子集都单独构成一棵树，它们都是根的子树（subtree）  

 

树的相关术语：

1）结点的度（degree）——其子树个数（某结点后面有多少条边）

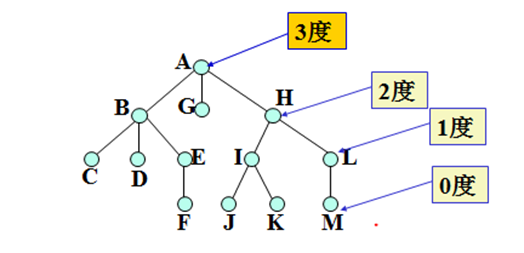
2）树的元数（way）——结点度数的最大允许值m

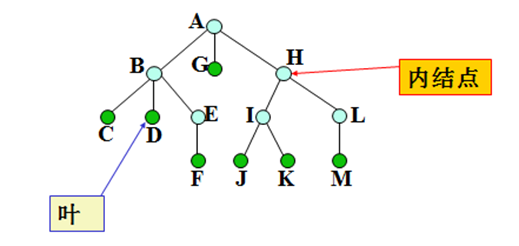
3）叶子（leaf）——度数为0的结点（也称终端结点），非叶结点又称为分枝点（或内结点）

 

4 、5 ）儿子（son）和父亲（father）

一个结点的子树之根称为该结点的儿子（儿子也称为孩子child，或子女）；若结点s是结点f的儿子，那么，f则是s的父亲（父亲也称双亲parent）

父结点也称前趋结点，子结点是后继结点

结点有一个前驱、多个后继——非线性结构

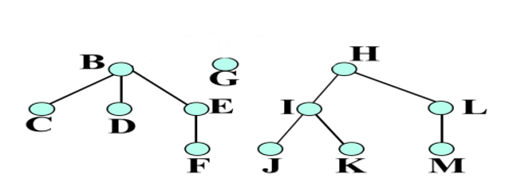
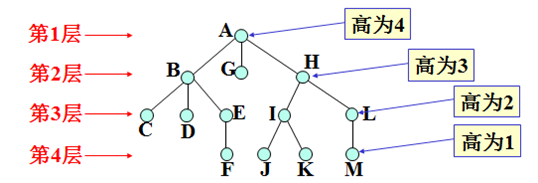
比如上图：A是B、G、H的双亲结点，而B、G、H是孩子结点。同理，E是F的双亲结点，而F是E的孩子结点。

6）兄弟（subling）——同父的结点互为兄弟

比如：因为A是B、G、H的双亲结点，所以B、G、H互称为兄弟结点。而E、I不是兄弟结点，因为两个结点前驱不是同一个（没有同父结点）。

7）子孙（descent）和真子孙（proper descent）

根为R的树（或子树）中所有结点都是R的子孙，除R本身之外，它们又都是R的真子孙 。

比如：B、G、H、C、D、E、F、I、L、J、K、M都是A的子孙结点，都有共同的祖先。子树为例，I、L、J、K、M也是H的子孙结点。

注意：子孙结点一般都要有3层以上的关系。

8）祖先（ancester）和真祖先（proper ancester）

根到结点V的路径上所有的结点都是V之祖先，除V本身之外，它们又都是V的真祖先。

9）路径（path） ——路径是结点序列，其中，任何两个相邻结点，前者是后者的父亲或儿子（简单路径）。

10）结点的层数（level） ——根的层数定为1，并递推地，第i层结点的儿子层数为i+1。

11）结点的高度（height）——所有叶子的高都定为1；递推地，非叶结点的高等于它各个儿子高度的最大值加1；树（包括子树）的高度等于其根的高度。

 

12）有序树和无序树

有序树：结点的儿子都必须按某种指定的次序排列

无序树：无上述要求（儿子可任意排列）

13）位置树——结点的各个儿子有固定位置

无序树条件下，三者相同

有序树条件下，树2和树3相同

3元位置树条件下，三者互不相同

14）森林（forest） ——树的集合称为森林，一个森林可包含0至多棵树