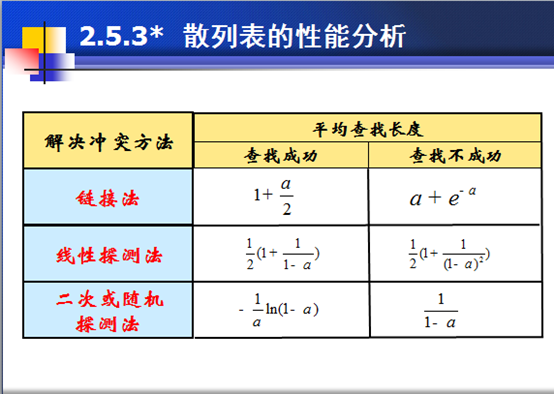
9散列表
散列表
或称Hash表或哈希表,通过科学的取地址方式,存放数据并便于查找。由此降低地址冲突的一个数据模式。
算法的实质:
完成 元素值x—>存储地址d的变换f,即 d=f(x)
(1)直接地址存储法
条件:元素取值范围与集合大小n差不多。
比如:定义数组arr[10],来存放10个自然数。
(2)散列存储法
条件:元素取值范围远远大于集合元素个数n。
比如:定义数组arr[10],来存放5个自然数。那么又怎么存放时最合理的,最利于查询的?这也是散列表的作用。
基本做法:
用数组a[m] 存储n个元素(m≥n)
存储元素x时,通过计算x的散列函数值:
h=hash(x) //0≤h≤m-1,将元素x存储在a[h]中
若任何xy,都有hash(x)hash(y),所设计的散列函数很均匀。查找x时,就能在a[hash(x)]中找到元素x。如果xy,而hash(x)=hash(y),则称x与y发生了碰撞 (Collision),或冲突。需要解决冲突。
下面介绍五种常用方法:
1. 取余法
2.提取数位法
3.平方取中法
4.折叠法
5.变换基数法
1.取余法
散列公式形如:hash(x)=x mod p
注意:
1. 模数p选取不大于m的常数 (m为数组的长度)。
2. 0≤hash(x)≤p-1≤m-1,保证地址不越界!
3. 通常情况下,模数p是一个接近m的最大素数时,散列结果比较均匀。
例如:元素个数n≤1000,散列表长度m=1024
取模数p=1019
hash(19450219)=566
hash(19761203)=755
2.提取数位法
一个很大数值按一定规律提取几个位数上的数字,组成一个新的数字,来代表这个数组。或者数值可能很小,也是利用二进制、八进制、十六进制等方式来提取。如图:
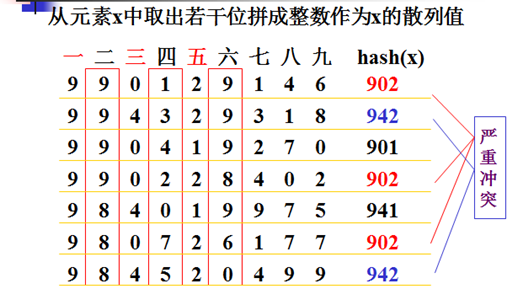
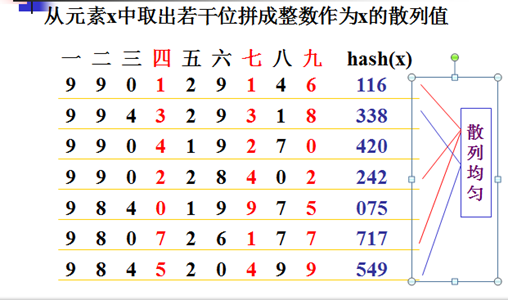
3.平方取中法
该方法就是第一、二种方法相结合,让原来的数值平方后,在按第二种方式随机取几位数再组成一个新的地址。这方法的平法的可能会很大。不常用,在此就不再加以介绍。
4.折叠法
把元素x分成若干段,折叠后相加作为x的散列地址
折叠方向:顺向,反向,或者正反向交替
相加:算术相加(带进位加法)
按位相加(无进位加法)
例如,x=64912387(八位十进制),取三位地址
几种不同的折叠方向和相加方法结果如下:
基本方法:分三段,每段三位,不足三位空缺
第一种移位叠加法----每部分最低位对齐
将x=64912387分成649、123和87,两种相加方法

第二种折界叠加法----沿分割界来回对折,对齐相加
将x=64912387分成649、321和87,两种相加方法

注意:x=6491238分成649、321和87,此时将中间一段反向,即123变成321。
第三种折叠方法:
将x=64912387分成64、219和783,两种相加方法
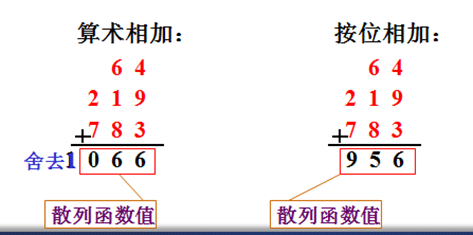
注意:将x=64912387分成64、219和783,此时将后面的两段反向,即912变成219,387变成783.
三种方法的比较:
这三种方法的本质是一样 ,把一个数拆分成几段,正向或反向部分,如:第一种:正向,不需要折叠,只把原数拆分;第二种:反向,将中间的部分反向;第三种:反向,将后面的两段反向。要注意:这方法的拆分是自拟的,第一、二种从左边开始,而第三种则从右边开始,根据个人习惯爱好。
5.变换基数法
将十进制数x看作其他进制(比如十三进制),再按十三进制数转换成十进制数,提取其中若干位作为x的散列值。
例如,
hash(80127429)10-----十进制
=( 80127429)13=8×137+0×136+1×135+2×134+7×133+4×132+2×13+9
=(502432641)10
再从(502432641)10这十进制数中任选几位作为散列函数。如:中间三位432.
6.混合法
将几种方法混合使用,比如,先变基,再折叠,再平方取中。。。
散列表的处理算法
1.构造和插入
构造:从空表开始,逐一插入
插入:通过计算元素x的散列函数值和解决冲突方法,为x找到一个空单元,存储x。
2.查找
查找:通过计算元素x的散列函数值和解决冲突方法,沿着x的插入路径就能找到x,插入路径就是查找路径,插入算法和查找算法步骤大体相同,
散列表的查找算法
步骤1)计算散列函数值h=hash(x);
步骤2)if(a[h]==x)return h; //查找成功
步骤3)if(a[h]==0)return 返回查找失败信息;
步骤4)按插入时采用的冲突处理方法进行查找
处理冲突
在上面提过,设计散列函数时不可能完全不冲突,因此就要处理这些冲突,有以下方法:
1. 链接法:将互相冲突的元素构成一个链表(处理方法同一般链表)
2. 开放地址法(二次散列法)
基本方法:
当发生冲突时,反复用探测的方法在散列表中寻找下一个结点
插入时,遇到空白结点即可进行插入。
查找时,直至找到要查找的元素(查找成功)。若遇到空白结点,表示查找失败。
第一种:线性探测具体步骤如图:






线性探测的特点
优点:简单,可环视一周寻找空单元
缺点:易产生聚集现象,增加“冲突链”长度
二次散列效果不佳
原因:增量的“步长”为1
改进措施:加大步长
第二种:平方探测的具体步骤:



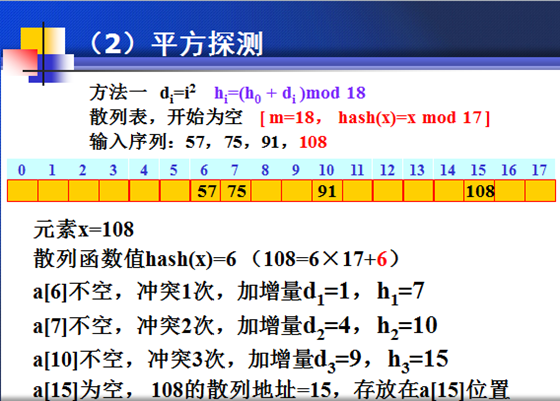

第二种:法二:平方探测的改进步骤:


第三种:随机探测的具体步骤:





散列表的删除方法(与解决冲突的方法有关)
1.使用链接法解决冲突时,与一般链表删除方法相似
2.用开放地址法解决冲突时,较难删除
(1)不能简单地置删除结点为空,这样会切断探测“链”
(2)可以对删除结点作“已删除标记”
查找时跳过这些结点;插入时可以重新使用这些结点
(3)定期对整个表重新散列