7矩阵
稀疏矩阵的顺序存储
在工程数学上学过矩阵,有多行多列,类似于多维数组。那么又如何将矩阵中的数值转换成数组的元素?
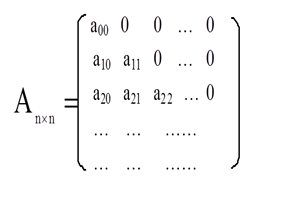
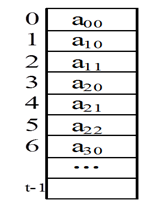
如图,左一是一个下三角矩阵,要将不为0的数值存放到一维数值中(右一)。
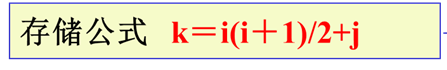
其中i是原矩阵的行标,j是原矩阵的列标,k是转换后数组的下标。
一般的非0元素极少可以用压缩法存储。。。
每个非0元素对应一个三元组(行号,列号,值)
(row,col,val)
若稀疏矩阵Am×n共有t个非0元素
t个三元组构成长度为t的线性表
矩阵运算可通过线性表运算实现
存储结构的定义:
#define m 100 //非0元素个数
typedef struct element
{ float val; //值域
int row, col;
} elem;
elem b[m]; // 定义存储数组
按行次序压缩顺序存储(按行顺序压缩存储)

稀疏矩阵的链式存储
链式存储有以下的几种方式:
(1)简单链式存储

(2)行链表组
结点只含列号域、元素域值和链域
适用于按行读取元素
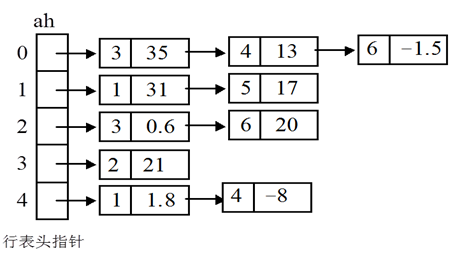
(3)正交链表
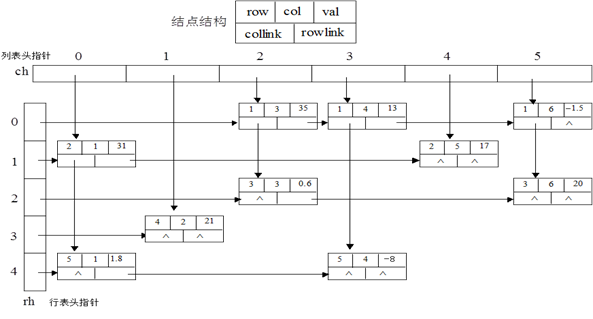
正交链表,其实就是二维数组+链表。
可以把rh,ch当成二维数组,再在二维数组中存储对应的结点。(结点中定义矩阵的数值属性,如结点结构所示)
不解之处:
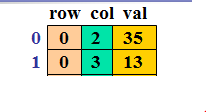
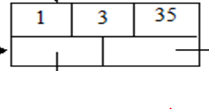
图一 图二
Val=35的行标row=0,列标col=2,但是在图二中的行标和列标却变成了1,3。为什么存储在结点的行、列标都+1,而不用原来的矩阵的行、列标。这是为什么?
矩阵的转置
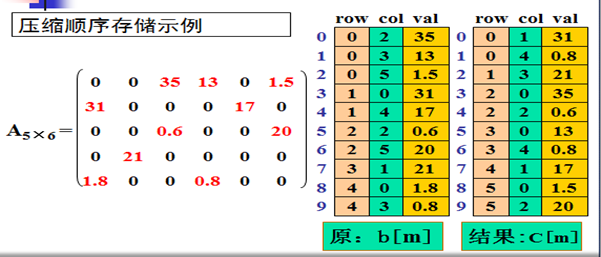
矩阵的转置有以下三种方式:
1.简单复制:
算法:
for(i=0;i<t;i++)
{
c[i].row=b[i].col;
c[i].col=b[i].row;
c[i].val=b[i].val;
}
从第一个元素开始,无论是否0都进行转置,效率有点低。
(2)逐行复制法
先转A的第一列非0元素
再转A的第二列非0元素
……
效率性:每转置一列,需要循环t次
A共n列,总共需要循环n*t次
转置共需O(nt)时间,效率也有点低
算法:
按行号j从0变到n-1,依次复制AT的各行非0元素
for(j=0;j<n;j++) //n是A的列数
for(i=0;i<t;i++)
if(b[i].col==j) //若列号是j
{ c[k].row=b[i].col; //原行号变为列号
c[k].col=b[i].row; //原列号变为行号
c[k++].val=b[i].val;
}
(3) 分段定位法(高效率)
该方法分为2个阶段:
1.预处理阶段
[1]统计A的各列非0元素个数,记录在数组num[n]中
[2]将数组c分成n段,使第j段含有num[j]个单元 ,用行定位指针数组pot[n]指示各段地址。
行定位指针的计算公式 :
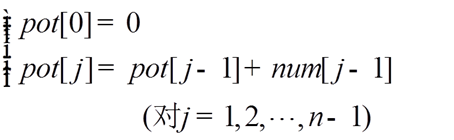
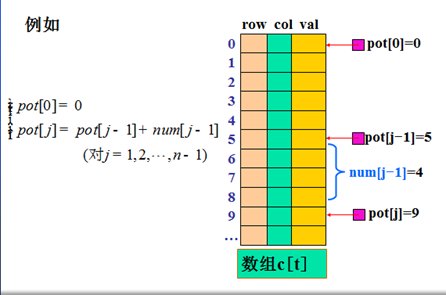
2.转置阶段
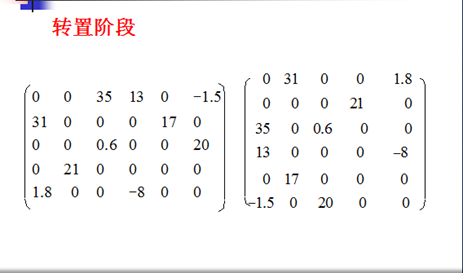
算法跟踪示例

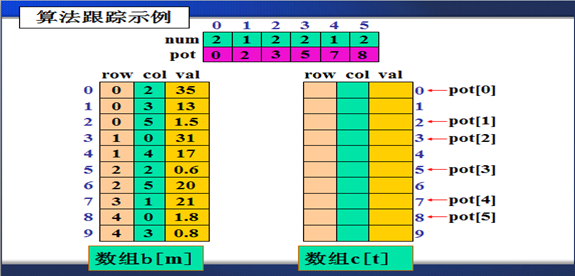
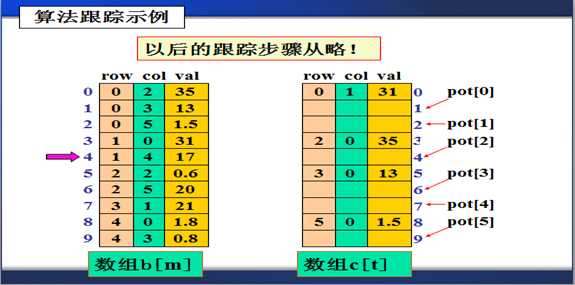
稀疏矩阵转置算法:
void transpose(elem b[ ],elem c[ ])
{
int i,j,k,num[n],pot[n];
for(j=0; j<n; j++)
num[j]=0; // 预处理阶段
for(i=0; i<t; i++)
num[b[i].col]++;
for(pot[0]=0,j=1;j<n;j++)
pot[j]=pot[j-1]+num[j-1];
for(i=0; i<t; i++) //转置阶段
{
j=b[i].col; //取列号
k=pot[j]; //取行定位指针值
c[k].row=j, c[k].col=b[i].row, c[k].val=b[i].val;
pot[j]++; //修改定位指针
}
}
该算法效率分析:

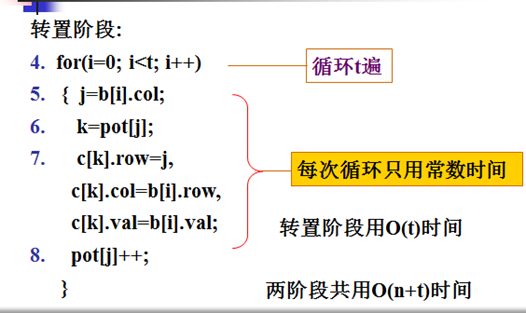
空间复杂性
使用两个辅助数组(数组num和数组pot)
各占O(n)个单元,故S(n)=O(n)
时间复杂性
预处理阶段,用O(n+t)时间
转置阶段,用O(t)时间
共用O(n+t)时间
稀疏矩阵相乘
本例采用逐步累加法
[1]先将Z的各元素存储单元c[i,j]清0
[2]顺序地扫描数a,每找到一个非元素xrk
在数组b中找出行号等于k的非0元素:
yks1,yks2,…
让xrk依次与它们相乘
乘积分别累加到c[r-1][s1-1],c[r-1][s2-1],······
用行定位指针pot[k]指向Y第k+1行非0元素在数组b中的存储位置(如下图)。
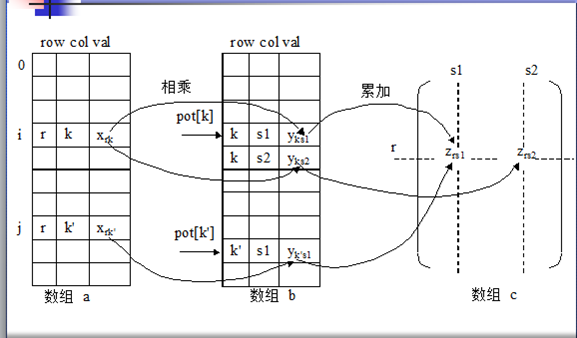
稀疏矩阵相乘算法:
void multiply(elem a[ ],elem b[ ],float c[ ][l])
{
int i,j,k,r,s,pot[n]; float x,y;
for(i=0; i<m; i++)
{
for(j=0; j<l; j++)
c[i][j]=0;
}
for(i=0; i<n; i++)
pot[i]=-1;
for(i=t2-1; i>=0; i--)
pot[b[i].row-1]=i;
for(i=0; i<t1; i++)
{
k=a[i].col;
j=pot[k-1];
if(j<0)continue;
r=a[i].row;
x=a[i].val;
while (b[j].row==k)
{
s=b[j].col;
y=b[j].val;
c[r-1][s-1]+=x*y;
j++;
}
}
}
该算法的效率分析:
空间复杂性
不计原始数据及结果数据所占空间
行定位指针数组pot占用O(n)个单元
“纯”空间复杂性S(n)=O(n)
时间复杂性
句1用O(ml)时间
句2用O(n)时间,句3用O(t2)时间
故,预处理阶段共用O(ml+n+t2)时间
相乘阶段
外循环(句4)执行t1次
内循环(句10)最多执行min(t2,l)次
句4到句14所用时间总量不超过
O(t1)O(min(t2,l))
两阶段所用时间相加
T(n)≤O(ml+n+t2+t1*min(t2,l))



