逆向知识第六讲,取摸优化的几种方式
除法讲完之后,直接开始讲 % 运算符在汇编中表现形式
首先C的高级代码贴上来.
高级代码:
// Tedy.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
int main(int argc, char* argv[])
{
unsigned Number;
scanf("%d",&Number); //防止常量传播
printf("%ud \r\n",Number % 8);//无符号/2的幂
__asm
{
nop;
nop; ;内联汇编,观看的时候知道怎么看
nop;
}
printf("%d",Number % 3);//无符号/非二的幂
__asm
{
nop;
nop;
nop;
}
printf("%d" , 8 % Number);//常量/变量
__asm
{
nop;
nop;
nop;
}
printf("%d",argc % 8);//有符号/2的幂
__asm
{
nop;
nop;
nop;
}
printf("%d",argc %-8);//有符号/2的幂,除数为负数
__asm
{
nop;
nop;
nop;
}
printf("%d",argc %3);//有符号/非2的幂
return 0;
}
一丶无符号% 2的幂在汇编中的表现形式
汇编代码:
高级对应语句:
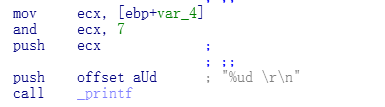
printf("%ud \r\n",Number % 8);
可以看出,当无符号%2的幂的时候,直接用and计算. 其值是 2^n - 1的值
比如我们的number %8,那么and的值则是 8-1,而8是2^3次方.
现在说下7这个数, 0111 它正好是3个指数位,所以还原的时候,直接看占的二进制位数,占了几位就是指数是多少.
需要注意:
我们一般看%某某个数的时候,我们要知道其结果保存在edx寄存器当中,而eax寄存器保存的是商
比如:
8 % 6 = 1 ..... 2 那么其值 1在eax中,其余数2在edx中
二丶无符号/非二的幂
高级代码:
printf("%d",Number % 3);//无符号/非二的幂
汇编代码:
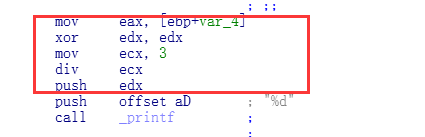
可以看出,无符号 / 非2的幂的时候,直接使用 DIV 了,同理有符号 / 非2的幂的时候,就会使用IDIV了.
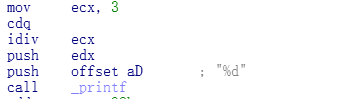
这个时候还原 除数则看 给的除数是多少了.
比如这里 DIV ecx,而ecx给的是3,则除数是3了.
还可以看到,这个地方 push的edx,那么说明使用的edx,而上面也说了,edx中的值存放的是余数的值.
三丶常量 % 变量
高级代码:
printf("%d" , 8 % Number);
汇编代码:
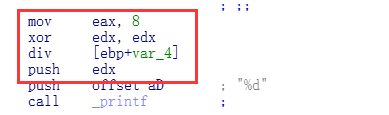
可以看出这段汇编代码, eax给的是常量,直接使用DIV了,用的是EDX,由此判定, 除数是一个变量,而这个变量是无符号类型了,因为上面的 XOR EDX,EDX清空了.
看到这一段代码的时候,还原手法:
eax % [ebp + var_4] = xxx ... edx
代入公式得:
8 % 变量 = 商...余数.
如果你知道变量是具体的值,比如现在是3
那么8 % 3 = 商...余数 即可.
四丶重点: 有符号 % 2的幂
高级代码:
printf("%d",argc % 8);//有符号/2的幂
汇编代码:
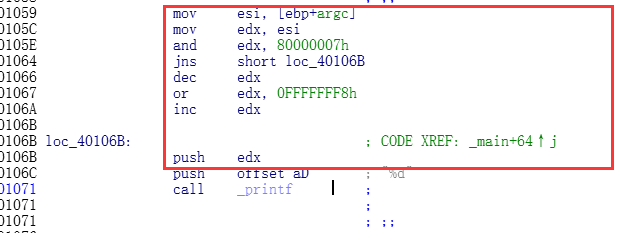
有符号的处理,比无符号复杂一些.主要判断一下符号位.
比如上面的高级代码对应的这些汇编代码.看不懂没关系.依次讲解.
我们知道有符号%一个数的时候,需要判断符号位对吧
那么此时分为三部分去看.
第一部分 : 正数的情况下
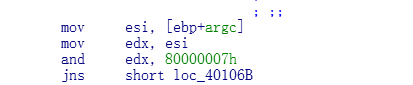
上面汇编代码表示, 我用有符号变量 % 一个80000007h,得出的结果如果不是负数(jns)那么余数就是正数,直接跳走了
首先我说下为什么是 800...7h
上面也说过了,要保留符号位
那么8则是符号位,也就是1, 而为什么最后是7那?,这个则是保留指数位.
800...7h换算成二进制表达形式为:
10000000000000000000000000000111
高位为符号位,低3位为指数位(当然不是固定的,它的指数位是 2^n-1,比如我们的除数为8,那么指数位则是 2^3 - 1 = 7,而7正好是占3个指数位,比如是16,那么2^4 - 1 = 15,而15的指数位则是占了4个二进制位)
这一段汇编代码,是计算正数的
假设我们的argc有符号变量为9
那么9对应的二进制则为
00000000000000000000000000001001
and (那么与刚才的二进制去 &(与)一下结果还是正数)
10000000000000000000000000000111
=
00000000000000000000000000000001 那么其值结果为1,也就是余数为1,而不是负数,此时就可以跳走直接运算了.
第二部分: 负数的情况下
上面说了正数的情况下,你直接and 2^n-1 的值即可.那么得出的结果还是正数.
那么现在是负数额情况下.

我们看到一个16进制的数字 0FFFFFFF8h,那么是什么意思那?
当然对应的二进制表达方式也写出来.
11111111111111111111111111111000
此时看汇编代码 ,注意 dec inc这些是特殊情况下需要用到的,暂时不管,现在只看 中间的or指令.
我们试想一下,如果我们余数是负数的情况下,
举例子:
-9 % 8 = 1 ... -1
也就是上面判断为正数的先走一遍.得到的余数二进制为 -1
那么对应二进制也就是
100000000000000000000000000000001 (现在的EDX的值).
然后现在有or了一下0FFFFFFF8h 这个值,那么说下这个怎么得到的.
我们上面说过了,保留了符号位,符号位置为1,还有保留指数位 (2^n - 1)
那么这个时候, 这个值就是 把中间的值变为1,保留(2^n-1的位数)
11111111111111111111111111111000
高位一个符号位,中间的0变为1,最后三个则是指数位,此时or之后
10000000000000000000000000001
or(或 |)
11111111111111111111111111111000
=
1000000000000000000000000001
那么则得出结果是 -1
第三部分: 特殊情况下
特殊情况下,则是 一个 dec,然后最后一个inc回来的时候.
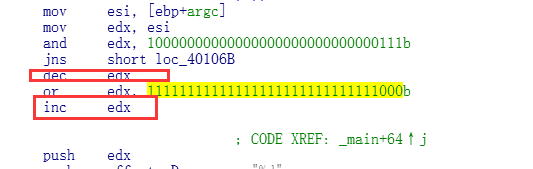
这个则是当余数为0的情况下才会触发.
比如 8 % 8 = 0;
走第一部分汇编代码的时候,edx里面的值都是0了.
然后-1,继续or, or出来的结果加1还是0.这个主要是余数为0的情况下.
重点: 还原手法
上面只是说的原理.(其实也不算高深点的原理,这里是站在汇编代码的角度下说的,其实真正的都有数学定理和公式)
以后凡是看到这块汇编代码:
我们直接看指数位是多少位即可. 比如上面我们%8,那么指数位是3个,那么还原的时候就是 r = 2^n次方即可.
n = 指数位
n = 3
如果计算上面的余数则
r = 2^ 3
r = 8即可.
当然我们要看一下最后用的寄存器是不是edx,如果是edx,那么就是 %,如果是用的eax,那么结果就是 /
很显然上面是用的edx,
还原回来的汇编代码为:
[ebp + argc] % 2^n
有符号局部变量 % 8 即可.
五丶有符号 % -2的幂
高级代码:
printf("%d",argc %-8);//有符号/2的幂,除数为负数
对应汇编代码:

首先在讲解之前,我们要明白一下.
我们举例子:
8 % 6 = 1 ... 2
8 %-6 = -1.....2
但是我们看一下,我们的余数并没有改变其结果, 余数都是2
比如我们列一个公式
a(被除数) b(除数) q(商) r (余数)
a % b = q ... r 这个是基本的.
那么
a % |b| = |q| ... r 摸不摸 b的绝对值,其 r值不变的.影响的只是 q对不起.
但是
|a| % b = |q| ...|r| 那么这个时候,如果把a变为绝对值,那么绝对会影响r的值.
上面的汇编代码.则是写了一个无分支求绝对值而已.如果数学公式搞懂了,那么看上面的汇编代码则会懂了
第一部分,无分支求绝对值

这个则是无分支求绝对值的代码.
首先esi的值是上面 argc局部变量的值,只不过上下文中没有修改esi,所以在这里直接使用.这里就想象成一个变量
然后CDQ, edx的值,跟随者eax的符号位填充,如果 eax(也就是现在变量的值是正数,那么eax的高位则是0,那么edx的值全部都是0)
如果是正数的情况下:
正数的情况下,eax是正数,edx因为符号扩展,所以结果是0, xor之后,其结果还是原值.
此时 原值 eax - edx (相当于, - 0 )那么其结果还是原值.
然后
此时把除数变为正数了,那么 直接使用and 7即可.(7是 2^n-1的值)
and之后,其eax的值则是余数(这里不是EDX了,有时候我们要看,这里是eax去弄得,所以放到里面了)
and之后,下方继续几行汇编代码,这些汇编代码都一样得出的结果还是原来的值.
如果是负数的情况下:
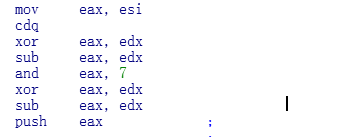
汇编代码就是这么一大堆.
然后负数的情况下,执行完求绝对值的代码之后,其结果就变成了正数. 在and eax,7上面弄得.
那么此时如果原来是负数的情况下,那么下方继续再来一遍,变为负数.
那么此时得出的除数是负数. 也就是 b为负数.(除数)
还原手法:
不管怎么做,上面先把绝对值求出来,然后和 (2^n-1)去and,此时得出了除数是 (2^n) ,那么怎么判断正数还是负数.
判断下方是否在取反了即可.
转载于:
作者:IBinary
出处:http://www.cnblogs.com/iBinary/



