逆向课程第四讲逆向中的优化方式,除法原理,以及除法优化上
一丶为什么要熟悉除法的优化,以及除法原理
是这样的,在计算机中,除法运算对应的汇编指令分为 DIV(无符号除法指令) 以及 IDIV(有符号除法指令).
但是,除法指令的执行周期较长效率很低.所以编译器想进办法的用其它指令去代替除法指令.
比如:
DIV 指令是100个周期
计算 2 / 2
那么可能在汇编中的表现形式是这样的
CDQ 符号扩展
DIV EDX,2
好,现在100个周期没有了
减法和加法指令,指令周期是4个那么上面的公式可以演化为
mov eax,2
sub eax,2
就算mov 指令是10个指令,那么总共计算起来才14个指令,而正好完成了一个除法
如果我们把指令周期看做时间的话,那么100个指令周期是100秒,14个指令周期是14秒
那么是不是时间变快了,那么相应的软件运行速度以及启动速度也变快了.
二丶丶熟悉数学证明
在讲解除法之前,我们要熟悉一下数学公式,以及数学证明,因为在除法的优化中,和这些数学公式息息相关.
当然你不看证明也可以,但是公式一定要明白
这里我讲解的是 <<C++反汇编与逆向分析技术揭秘>> 作者: 钱林松 赵海旭
伟大的钱老师的著作. 第47页
首先我们要明白计算机中的除法
1.有符号树和无符号数混除,那么结果是无符号的
2.两个无符号整数相除,结果还是无符号的.
3.计算机中面临如何处理小数,比如 9 / 4 = 2.25
理解数学中的向下取整,以及向上取整
向下取整:
讲道理: 比如对x向下取整, x>=0 那么就是 取得不大于x的最大整数, 相反也就是说, 小于x的遇到的第一个整数
比如 x = 5
那么向下取整则是4
不大于5,那么就是小于5, 然后遇到的最大整数,也就是4
向上取整:
同理,向上取整则是 不小于x的最大整数.
除法的扩展知识:
在整数的处罚中,只有能整除和不能整除的两种情况(废话)不能整除,则会产生余数.
设 a = 被除数 b = 除数 c = 商 r = 余数
那么可以得到下面的公式:
除法原型:
a / b = c .... r
6 / 4 = 1 ...2
1. |r| < |b| : 余数的绝对值,绝对会小于除数的. 比如 6 / 4 = 1 .... 2 那么 余数2 不关是正数还是父数,绝对都是绝对会小于除数的,也就是4
2. a = c * b + r : 求被除数,被除数是商*除数+余数
3.b = (a - r)/c : 求除数,除数等于 被除数-余数 / 商
4.c = (a - r)/b : 求商: 被除数 - 余数 / 除数
5. r = a - (c * b) : 求余数 被除数 - (商 * 除数)
3.计算机中的除法
1.当除数为变量,的时候
计算机中.的汇编指令为 DIV 或者 IDIV,因为除数是不确定的
比如:
int n ;
7 / n ===> 汇编指令就用DIV 或者IDIV
没有优化的余地,看汇编代码.
除数为有符号相除

除数为无符号

当除数为变量,且分为有符号和无符号相除
有符号相除: 那么使用的汇编指令是IDIV
无符号相除: 那么使用的汇编指令是DIV
2.当除数为2的幂的时候被除数分为有符号和无符号位的时候
比如代码为:
被除数无符号的情况下,除数是2的幂次方: (也就是n是无符号)
n / 8 那么8是2^3次方
那么直接优化为 shr
左移三位

被除数有符号的情况下且大于0,除数是2的幂次方

看到汇编代码懵逼,那么上公式,证明,然后则明白
首先公式等于

当B (除数)大于0则使用上面的公式,当b < 0则使用下面的公式
比如计算机中,被除数为正数的时候,可以使用第一个公式的第一个,也可以使用第二个,不过计算机默认向0取整
比如我们计算 17 / 8
正常计算 17 / 8 = 2 .xxxx
有小数
不过计算机计算出来的结果则是2,省略小数了,那么计算机使用的则是第一个公式.
a / b 向下取整, 然后也可以 a - b + 1 / b 向上取整
我们实验一下,
代入得到
17 - 8 + 1 / 8 =
10 / 8 = 1.25 转化为后面的公式,向上取整则是2了.
那么上面的汇编代码应该能看明白了.

首先 Cdq 是符号扩展的意思,也就是EDX和EAX一起使用,变成了一个64位寄存器.
然后利用and和edx比较7, 这个7怎么的出来了,这个7就是上面我们用第一个公式计算出来的
也就是 a - b + 1 这个, 这个7则是b + 1的值.
然后 add eax,edx 被除数 + 上 and过后的值.
最后右边移动三位.
这里编译器巧妙的利用 cdq符号扩展,然后利用了公式,进行了无分支判断.
如果我们的被除数是正数,那么 符号扩展之后,edx的值则全部是0,然后and过后,结果还是0
那么我们的被除数 + 0 右移3位 然后向下取整.
比如我们计算的 n / 8
n取值为17
那么计算的出 b + 1 的值为 8 + 1
那么是正数,则edx为0,and 9之后还是0
那么下面直接 add eax,edx
eax = 原来的被除数 也就是17
edx 结果and后为0
那么结果还是17
最后 17 右移动三位则是 2.xxx 向下取整就是2了.
如果是负数,那么b+1的值还是9
那么此时 add eax,edx = -17 + b - 1 = -10
而后 -10 右移动3位 (-10 / 8) = 1.25 此时向上取整,结果还是-2
公式的话,主要看计算机,一般计算机整数相除,选择向下取整
负数相除,选择向上取整.
3.无符号是被除数的情况下, 除数为非2的幂的时候
比如高级语言
unsigned int a;
a / 3 那么汇编指令有不一样了
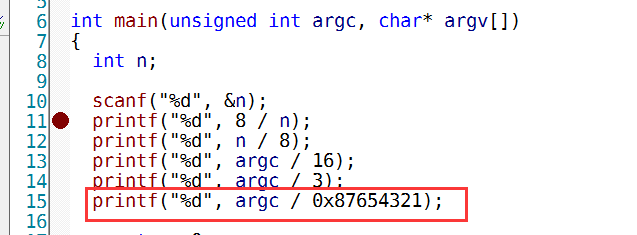
我们看下最后两个, /3 的,还有/ 0x87654321的

优化成了这样,还是没有看到除法
a /c C为常量的时候 a(被除数)
那么可以得出公式 am >> n位 (具体的推导公式就不写了,反正都是记公式)
其中m = 2n / c (n的取值范围看系统,如果是16位,那么n的起步就是16 ,32位则是32位起步)
那么现在
mov eax ,xxxxx xxxx是m
mul reg32
shr edx,1fh 1fh是n
那么根据上面的公式 am >> n
现在已经知道n和m了
而 m = 2n / c
那么现在可以求C了
按照最后一个求得出 n = 1f ,也就是2^1f + 2^32
为什么要加上2^32,因为 EDX和eax现在是一个64位寄存器,(看作是)符号扩展了,EDX移动一位,那么相当于eax 移动33位.
m = 0f2044d73
现在求C的值
反推即可
C = 2^n / m
转为十进制计算
9223372036854775808 / 4060368243 = 2271560480.4455111112443010011986
结果向上取整得出2271560481
转为16进制得出

顺利还原代码.
转载于:
作者:IBinary
出处:http://www.cnblogs.com/iBinary/




