19图的搜索算法总结与比较

图的搜索算法小结

1．深度优先搜索与广度优先搜索算法有何区别

       通常深度优先搜索法不全部保留结点，扩展完的结点从数据存储结构栈中弹出删去，这样，一般在数据栈中存储的结点数就是解空间树的深度，因此它占用空间较少。所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。
　　广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些。

2．回溯与分支限界法

       回溯法以深度优先的方式搜索解空间树T，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树T。由于它们在问题的解空间树T上搜索的方法不同，适合解决的问题也就不同。一般情况下，回溯法的求解目标是找出T中满足约束条件的所有解的方案，而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出使用某一目标函数值达到极大或极小的解，即在某种意义下的最优解。相对而言，分支限界算法的解空间比回溯法大得多， 因此当内存容量有限时，回溯法成功的可能性更大。

  下表列出了回溯法和分支限界法的一些区别：

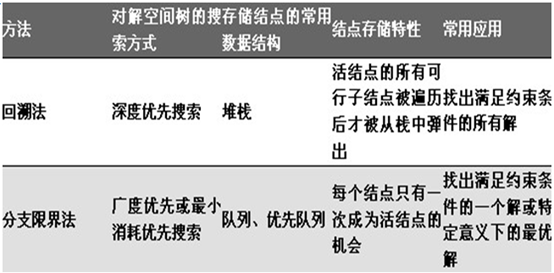
　　在处理最优问题时，采用穷举法、回溯法或分支限界法都可以通过利用当前最优解和上界函数加速。仅就对限界剪支的效率而言，优先队列的分支限界法显然要更充分一些。在穷举法中通过上界函数与当前情况下函数值的比较可以直接略过不合要求的情况而省去了更进一步的枚举和判断；回溯法则因为层次的划分，可以在上界函数值小于当前最优解时，剪去以该结点为根的子树，也就是节省了搜索范围；分支限界法在这方面除了可以做到回溯法能做到的之外，同时若采用优先队列的分支限界法，用上界函数作为活结点的优先级，一旦有叶结点成为当前扩展结点，就意味着该叶结点所对应的解即为最优解，可以立即终止其余的过程。在前面的例题中曾说明，优先队列的分支限界法更象是有选择、有目的地进行深度优先搜索，时间效率、空间效率都是比较高的。

 

3．动态规划与搜索算法

      撇开时空效率的因素不谈，在解决最优化问题的算法中，搜索可以说是“万能”的。所以动态规划可以解决的问题，搜索也一定可以解决。动态规划要求阶段决策具有无后向性，而搜索算法没有此限止。

       动态规划是自底向上的递推求解，而无论深度优先搜索或广度优先搜索都是自顶向下求解。利用动态规划法进行算法设计时，设计者在进行算法设计前已经用大脑自己构造好了问题的解空间，因此可以自底向上的递推求解；而搜索算法是在搜索过程中根据一定规则自动构造，并搜索解空间树的。由于在很多情况下，问题的解空间太复杂用大脑构造有一定困难，仍然需要采用搜索算法。

      另外动态规划在递推求解过程中，需要用数组存储有关信息，而数组的下标只能是整数，所以要求问题中相关的数据必须为整数（如4.5.3节【例2】“资源分配问题”中的资金就必须为整数），对于这类信息非整数或不便于转换为整数的问题，同样需要采用搜索算法。

      一般说来，动态规划算法在时间效率上的优势是搜索无法比拟的，但动态规划总要遍历所有的状态，而搜索可以排除一些无效状态。更重要的是搜索还可以剪枝，可能剪去大量不必要的状态，因此在空间开销上往往比动态规划要低很多。如何协调好动态规划的高效率与高消费之间的矛盾呢？有一种折衷的办法就是记忆化搜索算法

        记忆化限界搜索算法在求解时，还是按着自顶向下的顺序，但是每求解一个状态，就将它的解保存下来，以后再次遇到这个状态的时候，就不必重新求解了。这种方法综合了搜索和动态规划两方面的优点，因而还是很有实用价值的。记忆化限界搜索。它以搜索算法为核心，只不过使用“记录求过的状态”的办法，来避免重复搜索，这样，记忆化搜索的每一步，也可以对应到动态规划算法中去。记忆化搜索有优化方便、调试容易、思维直观的优点，但是效率上比循环的动态规划差一个常数，但是时间和空间复杂度是同一数量级的（尽管空间上也差一个常数，那就是堆栈空间）。当n比较小的时候，我们可以忽略这个常数，从而记忆化搜索可以和动态规划达到完全相同的效果。