18图的搜索算法之分支限界法
分支限界法
基本思想
分支搜索法也是一种在问题解空间上进行尝试搜索算法。所谓“分支”是采用广度优先的策略,依次生成E-结点所有分支,也就是所有的儿子结点。和回溯法一样,在生成的节点中,抛弃那些不满足约束条件(或者说不可能导出最优可行解)的结点,其余节点加入活节点表。然后从表中选择一个节点作为下一个E-节点。选择下一个E-节点的方式不同导致几种不同的分支搜索方式:
1)FIFO搜索
2)LIFO搜索
3)优先队列式搜索
1. FIFO搜索
一开始,根结点是唯一的活结点,根结点入队。从活结点队中取出根结点后,作为当前扩展结点。对当前扩展结点,先从左到右地产生它的所有儿子,用约束条件检查,把所有满足约束函数的儿子加入活结点队列中。再从活结点表中取出队首结点(队中最先进来的结点)为当前扩展结点,……,直到找到一个解或活结点队列为空为止。
2.LIFO搜索
一开始,根结点入栈。从栈中弹出一个结点为当前扩展结点。对当前扩展结点,先从左到右地产生它的所有儿子,用约束条件检查,把所有满足约束函数的儿子入栈,再从栈中弹出一个结点(栈中最后进来的结点)为当前扩展结点,……,直到找到一个解或栈为空为止。
3.优先队列式搜索
为了加速搜索的进程,应采用有效地方式选择E-结点进行扩展。优先队列式搜索,对每一活结点计算一个优先级(某些信息的函数值),并根据这些优先级,从当前活结点表中优先选择一个优先级最高(最有利)的结点作为扩展结点,使搜索朝着解空间树上有最优解的分支推进,以便尽快地找出一个最优解。这种扩展方式要到下一节才用的到。
分枝-限界搜索算法
【例2】有两艘船,n 个货箱。第一艘船的载重量是c1,第二艘船的载重量是c2,wi 是货箱i 的重量,且w 1+w2+……+wn≤c1+c2。
我们希望确定是否有一种可将所有n 个货箱全部装船的方法。若有的话,找出该方法

算法1的缺点有:
1)在可解的情况下,没有给出每艘装载物品的方案。而要想记录第一艘船最大装载的方案,象回溯法中用n个元素的数组是不能实现的,可以象5.2.2小节中的例子用数组队列下标记录解方案。
这里采用构造二叉树的方法,和5.2.2小节中的例题一样只需要记录最优解的叶结点,这样二叉树就必需有指向父结点的指针,以便从叶结点回溯找解的方案。又为了方便知道当前结点对物品的取舍情况,还必须记录当前结点是父结点的哪一个儿子。
数据结构:由此,树中结点的信息包括:weight;parent; LChild;。同时这些结点的地址就是抽象队列的元素,队列操作与算法1相同 .
2)算法1是在对子集树进行盲目搜索,我们虽然不能将搜索算法改进为多项式复杂度,但在算法中加入了“限界”技巧,还是能降低算法的复杂度。
一个简单的现象,若当前分支的“装载上界”,比现有的最大装载小,则该分支就无需继续搜索。而一个分支的“装载上界”,也是容易求解的,就是假设装载当前物品以后的所有物品。
举一个简单的例子,W={50,10,10},C1=60,所构成的子集树就无需搜索结点2的分支,因为扩展结点1后,就知道最大装载量不会小于50;而扩展结点2时,发现此分支的“装载上界”为w2+w3=20<50,无需搜索此分支,结点2不必入队。
数据结构:相应地,当前最大装载bestw不仅仅对叶结点计算,每次搜索装载情况(搜索左儿子)时,都重新确定bestw的值。为了方便计算一个分支的“装载上界”,用变量r记录当前层以下的最大重量。
公共变量的定义:
float bestw,w[100],bestx[100];
int n;
Queue Q;
struct QNode
{ float weight;
QNode *parent;
QNode LChild;}
算法如下:
main( )
{int c1,c2,n, s=0,i;
input(c1,c2,n);
for(i=1;i<=n;i++)
{input(w[i]); s=s+w[i];}
if (s<=c1 or s<=c2)
{print(“need only one ship”); return;}
if (s>c1+c2) {print(“no solution”); return;}
MaxLoading(c1);
if (s- bestw <=c2);
{print(“The first ship loading”, bestw,“chose:”);
for(i=1;i<=n;i++)
if(bestx[i]=1)
print(i,“,”);
print(“换行符 The second ship loading”, s-bestw,“chose”);
for(i=1;i<=n;i++)
if(bestx[i]=1)
print(i,”,”);
}
else
print(“no solution”);
}
AddLiveNode(folat wt,int i, QNode *E, int ch)
{ Qnode *b;
if (i = n) / 叶子
{ if (wt>bestw) / 目前的最优解/
{ bestE = E;
bestx[n] = ch;} //bestx[n]取值为ch
return; }
b = new QNode; // 不是叶子, 添加到队列中
b->weight = wt;
b->parent = E;
b->LChild = ch; //新节点是左孩子时
add (Q,b) ;
}
MaxLoading(int n, int bestx[])
{Qnode *E; int i = 1;
E= new QNode;add (Q,0) ; // 0 代表本层的尾部
E->weight=0; E->parent =null; E->Lchild=0; add (Q,E) ;
bestw = 0; r = 0; // E-节点中余下的重量
Ew=E->weight;
for (int j =2; j <= n; j++) r=r+ w[i];
while (true) // 搜索子集空间树
{ wt = E->weight + w[i]; // 检查E-节点的左孩子
if (wt <= c) // 可行的左孩子
{ if (wt > bestw)
bestw = wt;
AddLiveNode(wt,i, E ,1);}
if (Ew+r > bestw) // 检查右孩子
AddLiveNode(Ew,i,E,0);
Delete (Q,E ) ; // 下一个E-节点
if (!E) // 层的尾部
{if (Empty(Q ))
break;
add (Q 0 ) ; // 层尾指针
Delete(Q,E ) ; // 下一个E-节点
i + + ; // E-节点的层次
r = r - w[i];} // E-节点中余下的重量
Ew = E-> w e i g h t ; // 新的E-节点的重量
}
// 沿着从b e s t E到根的路径构造x[ ],x [n]由AddLiveNode来设置
for (j = n - 1; j > 0; j--)
{bestx[j] = bestE->LChild; // 从b o o l转换为i n t
bestE = bestE->parent;}
return bestw;
}
算法设计3:用优先队列式分支限界法解决【例2】的问题
介绍的优先队列式扩展方式,若不加入限界策略其实是无意义的。因为要说明解的最优性,不搜索完所有问题空间是不能下结论的,而要对问题空间进行完全搜索,考虑优先级也就没有意义了。
优先队列式搜索通过结点的优先级,可以使搜索尽快朝着解空间树上有最优解的分支推进,这样当前最优解一定较接近真正的最优解。其后我们将当前最优解作为一个“界”,对上界(或下界)不可能达到(大于)这个界的分支则不去进行搜索,这样就缩小搜索范围,提高了搜索效率。这种搜索策略称为优先队列式分支限界法——LC-检索。
1)结点扩展方式:无论那种分支限界法,都需要有一张活结点表。优先队列的分支限界法将活结点组织成一个优先队列,并按优先队列中规定的结点优先级选取优先级最高的下一个结点成为当前扩展结点。
2)结点优先级确定:优先队列中结点优先级常规定为一个与该结点相关的数值p,它一般表示其接近最优解的程度,本例题就以当前结点的所在分支的装载上界为优先值。
3)优先队列组织:结点优先级确定后,简单地按结点优先级进行排序,就生成了优先队列。排序算法的时间复杂度较高,考虑到搜索算法每次只扩展一个结点,回忆数据结构中堆排序,适合这一特点且比较交换的次数最少。此题应该采用最大堆来实现优先队列。
数据结构设计:
1)要输出解的方案,在搜索过程中仍需要生成解结构树,其结点信息包括指向父结点的指针和标识物品取舍(或是父结点的左、右孩子)。
2)堆结点首先应该包括结点优先级信息:结点的所在分支的装载上界uweight;堆中无法体现结点的层次信息(level),只能存储在结点中;
AddLiveNode用于把bbnode类型的活节点加到子树中,并把HeapNode类型的活节点插入最大堆。
3)不同与算法2,由于扩展结点不是按层进行的计算结点的所在分支的装载上界时,要用数组变量r记录当前层以下的最大重量,这样可以随时方便使用各层结点的装载上界。
同样为了突出算法本身的思想,对堆操作也只进行抽象的描述:用HeapNode代表队列类型,则HeapNode H;定义了一个堆H,相关操作有:Insert (Q,……)表示入堆; DeleteMax (Q,……);表示出堆。
算法3如下:
HeapNode H[1000];
struct bbnode
{bbnode *parent; // 父节点指针
int LChild; }; // 当且仅当是父节点的左孩子时,取值为1
struct HeapNode
{bbnode *ptr; // 活节点指针
float uweight; // 活节点的重量上限
int level; } ; // 活节点所在层
AddLiveNode(float wt, int lev,bbnode *E, int ch)
{bbnode *b = new bbnode;
b ->parent = E;
b->LChild = ch;
HeapNode N;
N.uweight = wt;
N.level=lev;
N.ptr=b;
Insert(H,N) ;
}
MaxLoading(float c, int n, int bestx[])
{froat r[100],Ew,bestw=0; r[n] = 0;
for (int j = n-1; j > 0; j--) r[j]=r[j+1] + w[j+1];
int i = 1; bbnode *E = 0; Ew = 0; // 搜索子集空间树
while (i != n+1) // 不在叶子上
{ if (Ew + w[i] <= c) // 可行的左孩子
{AddLiveNode(E, Ew+w[i]+r[i], 1, i+1);}
if (bestw<Ew+w[i]) bestw=Ew+w[i];
if(bestw<Ew+r[i]) AddLiveNode(E, Ew+r[i], 0, i+1);
DeleteMax(H,E);i=N.level;E=N.ptr; Ew=N.uweight-r[i-1];
}
for (int j = n; j > 0; j--)
{bestx[j] = E->LChild; E = E->parent;}
return Ew;
}
算法说明:
算法的复杂度仍为O(2n),但通过限界策略,并没有搜索子集树中的所有结点,且,由于每次都是选取的最接近最优解的结点扩展,所以一当搜索到叶结点作E结点时算法就可以结束了。算法结束时堆并不一定为空。
小结讨论:
FIFO搜索或LIFO搜索也可以通过加入“限界”策略加速搜索吗?那与优先队列式分支限界法——LC—检索的区别在哪儿呢?
答案:由于FIFO搜索或LIFO搜索是盲目扩展地结点,当前最优解距真正的最优解距离较大,作为“界”所起到的剪枝作用很有限,不能有效提高搜索速度。其实看了下面的例子大家会发现,优先队列式扩展结点的过程,一开始实际是在进行类似“深度优先”的搜索。
例如:W={10,30,50},C1=60, 所构成的子集树如下图所表示:
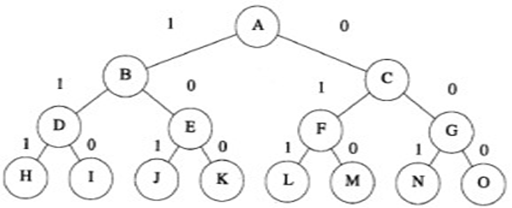
FIFO限界搜索过程为:
1) 初始队列中只有结点A;
2) 结点A变为E-结点扩充B入队,bestw=10;
结点C的装载上界为30+50=80> bestw,也入队;
3) 结点B变为E-结点扩充D入队,bestw=40;
结点E的装载上界为60> bestw,也入队;
4) 结点C变为E-结点扩充F入队,bestw仍为40;
结点G的装载上界为50> bestw,也入队;
5) 结点D变为E-结点,叶结点H超过容量,
叶结点I的装载为40,bestw仍为40;
6) 结点E变为E-结点,叶结点J装载量为60,bestw为60;
叶结点K被剪掉;
7) 结点F变为E-结点,叶结点L超过容量,bestw为60;
叶结点M被剪掉;
8) 结点G变为E-结点,叶结点N、O都被剪掉;
此时队列空算法结束。
LC-搜索的过程如下:
1) 初始队列中只有结点A;
2) 结点A变为E-结点扩充B入堆,bestw=10;
结点C的装载上界为30+50=80> bestw,也入堆;堆中B上界为90在优先队列首。
3) 结点B变为E-结点扩充D入堆,bestw=40;
结点E的装载上界为60> bestw,也入堆;此时堆中D上界为90为优先队列首。
4) 结点D变为E-结点,叶结点H超过容量,叶结点I的装载为40入堆,
bestw仍为40;此时堆中C上界为80为优先队列首。
5) 结点C变为E-结点扩充F入堆,bestw仍为40;
结点G的装载上界为50> bestw,也入堆;此时堆中E上界为60为优先队列首。
6) 结点E变为E-结点,叶结点J装载量为60入堆,bestw变为60;
叶结点K上界为10<bestw被剪掉;此时堆中J上界为60为优先队列首。
7) 结点J变为E-结点,扩展的层次为4算法结束。
虽然此时堆并不空,但可以确定已找到了最优解。
FIFO限界算法搜索解空间的过程是按图5-26子集树中字母序进行的,而优先队列限界搜索解空间的过程是:A-B-D-C-E-J
看了上面的例子大家会发现,优先队列法扩展结点的过程,一开始实际是在进行类似“深度优先”的搜索。
之前的例子是求最大值的最优化问题,下面我们以求找最小成本的最优化问题,给出FIFO分支搜索算法框架。
假定问题解空间树为T,T至少包含一个解结点(即答案结点)。u为当前的最优解,初值为一个较大的数;E表示当前扩展的活结点,x为E的儿子,s(x)为结点x下界函数,当其值比u大时,不可能为最优解,不继续搜索此分支,该结点不入队;当其值比u小时,可能达到最优解,继续搜索此分支,该结点入队;cost(X)为当前叶结点所在分支的解。
算法框架如下:
search(T) //为找出最小成本答案结点检索T。
{leaf=0;
初始化队;
ADDQ(T); //根结点入队
parent(E)=0; //记录扩展路径,当前结点的父结点
while
(队不空)
{DELETEQ(E) //队首结点出队为新的E结点;
for (E的每个儿子 X)
if (s(X)<u) //当是可能的最优解时入队
{ADD Q(X);
parent(X)=E;
if (X是解结点 ) //x为叶结点
{U=min(cost(X),u);
leaf=x;} //方案的叶结点存储在leaf中
}
}
print(”least cost=’,u);
while (leaf<>0) //输出最优解方案
{print(leaf);
leaf=parent(leaf);}
}
找最小成本的LC分支-限界算法框架与 FIFO分支-限界算法框架结构大致相同,只是扩展结点的顺序不同,因而存储活结点的数据结构不同。 FIFO分支-限界算法用队存储活结点,LC分支-限界算法用堆存储活结点,以保证比较优良的结点先被扩展。且对于LC分支-限界算法,一当扩展到叶结点就已经找到最优解,可以停止搜索。



