17图的搜索算法之回溯法
回 溯 法
回溯算法实际是一个类似枚举的搜索尝试方法,它的主题思想是在搜索尝试中找问题的解,当不满足求解条件就”回溯”返回,尝试别的路径。回溯算法是尝试搜索算法中最为基本的一种算法,其采用了一种“走不通就掉头”的思想,作为其控制结构。
【例1】八皇后问题模型建立
要在8*8的国际象棋棋盘中放八个皇后,使任意两个皇后都不能互相吃掉。规则:皇后能吃掉同一行、同一列、同一对角线的任意棋子。如图5-12为一种方案,求所有的解。

模型建立
不妨设八个皇后为xi,她们分别在第i行(i=1,2,3,4……,8),这样问题的解空间,就是一个八个皇后所在列的序号,为n元一维向量(x1,x2,x3,x4,x5,x6,x7,x8),搜索空间是1≤xi≤8(i=1,2,3,4……,8),共88个状态。约束条件是八个(1,x1),(2,x2) ,(3,x3),(4,x4) ,(5,x5), (6,x6) , (7,x7), (8,x8)不在同一行、同一列和同一对角线上。
虽然问题共有88个状态,但算法不会真正地搜索这么多的状态,因为前面已经说明,回溯法采用的是“走不通就掉头”的策略,而形如(1,1,x3,x4, x5,x6,x7,x8)的状态共有86个,由于1,2号皇后
在同一列不满足约束条件,回溯后这86个状态是不会搜索的。
算法设计1:加约束条件的枚举算法
最简单的算法就是通过八重循环模拟搜索空间中的88个状态,按深度优先思想,从第一个皇后从第一列开始搜索,每前进一步检查是否满足约束条件,不满足时,用continue语句回溯,满足满足约束条件,开始下一层循环,直到找出问题的解。
约束条件不在同一列的表达式为xi xj;而在同一主对角线上时xi-i=xj-j, 在同一负对角线上时xi+i=xj+j,因此,不在同一对角线上的约束条件表示为abs(xi-xj) abs(i-j)(abs()取绝对值)。
算法1:
queen1( )
{int a[9];
for (a[1]=1;a[1]<=8;a[1]++)
for (a[2]=1;a[2]<=8;a[2]++)
{if ( check(a,2)=0 ) continue;
for (a[3]=1;a[3]<=8;a[3]++)
{if(check(a,3)=0) continue;
for (a[4]=1;a[4]<=8;a[4]++)
{if (check(a,4)=0) continue;
for (a[5]=1;a[5]<=8;a[5]++)
{if (check(a,5)=0) continue;
for (a[6]=1;a[6]<=8;a[6]++)
{if (check(a,6)=0) continue;
for(a[7]=1;a[7]<=8;a[7]++)
{if (check(a,7)=0) continue;
for(a[8]=1;a[8]<=8;a[8]++)
{if (check(a,8)=0)
continue;
else
for(i=1;i<=8;i++)
print(a[i]);
}
} } } } } } }
check(int a[ ],int n)
{int i;
for(i=1;i<=n-1;i++)
if (abs(a[i]-a[n])=abs(i-n)) or (a[i]=a[n])
return(0);
return(1);
}
算法分析1:
若将算法中循环嵌套间的检查是否满足约束条件的:
“if (check(a[],i)=0)continue;
i=2,3,4,5,6,7“
语句都去掉,只保留最后一个检查语句:
“if (check(a[],8)=0)continue;”
相应地check()函数修改成:
check*(a[],n)
{int i,j;
for(i=2;i<=n;i++)
for(j=1;j<=i-1;j++)
if(abs(a[i]-a[j])=abs(i-j))or(a[i]=a[j])
return(0);
return(1);
}
则算法退化成完全的盲目搜索,复杂性就是88了
算法设计2:非递归回溯算法
以上的枚举算法可读性很好,但它只能解决八皇后问题,而不能解决任意的n皇后问题。下面的非递归算法可以说是典型的回溯算法模型。
算法2:
int a[20],n;
queen2( )
{
input(n);
backdate(n);
}
backdate (int n)
{ int k;
a[1]=0; k=1;
while( k>0 )
{a[k]=a[k]+1;
while ((a[k]<=n) and (check(k)=0)) /搜索第k个皇后位置/
a[k]=a[k]+1;
if( a[k]<=n)
if(k=n ) output(n); / 找到一组解/
else {k=k+1; 继续为第k+1个皇后找到位置/
a[k]=0;}/注意下一个皇后一定要从头开始搜索/
else k=k-1; /回溯/
}
}
check(int k)
{ int i;
for(i=1;i<=k-1;i++)
if (abs(a[i]-a[k])=abs(i-k)) or (a[i]=a[k])
return(0);
return(1);
}
output( )
{ int i;
for(i=1;i<=n;i++)
print(a[i]);
}
算法设计3:递归算法
这种方式也可以解决任意的n皇后问题。
这里我们用第三章3.2.3 “利用数组记录状态信息”的技巧,用三个数组c,b,d分别记录棋盘上的n个列、n个主对角线和n个负对角线的占用情况。
以四阶棋盘为例,如图5-13,共有2n-1=7个主对角线,对应地也有7个负对角线。
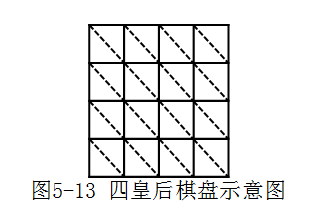
用i,j分别表示皇后所在的行列,同一主对角线上的行列下标的差一样,若用表达式i-j编号,则范围为-n+1——n-1,所以我们用表达式i-j+n对主对角线编号,范围就是1——2n-1。同样地,负对角线上行列下标的和一样,用表达式i+j编号,则范围为2——2n。
算法3:
int a[20],b[20],c[40],d[40];
int n,t,i,j,k; /t记录解的个数/
queen3( )
{ int i,
input(n);
for(i=1;i<=n;i++)
{ b[i]=0;
c[i]=0; c[n+i]=0;
d[i]=0; d[n+i]=0;
}
try(1);
}
try(int i)
{int j;
for(j=1;j<=n;j++) /第i个皇后有n种可能位置/
if (b[j]=0) and (c[i+j]=0) and (d[i-j+n]=0)
{a[i]=j; /摆放皇后/
b[j]=1; /占领第j列/
c[i+j]=1; d[i-j+n]=1; /占领两个对角线/
if (i<n)
try(i+1); /n个皇后没有摆完,递归摆放下一皇后/
else
output( ); /完成任务,打印结果/
b[j]=0; c[i+j]=0; d[i-j+n]=0; /回溯/
}
}
output( )
{ t=t+1;
print(t,' ');
for( k=1;k<=n;k++)
print(a[k],' ');
print(“ 换行符”);
}
递归算法的回溯是由函数调用结束自动完成的,也不需要指出回溯点,但也需要“清理现场”——将当前点占用的位置释放,也就是算法try()中的后三个赋值语句。
1. 回溯法基本思想
回溯法是在包含问题的所有解的解空间树中。按照深度优先的策略,从根结点出发搜索解空间树,算法搜索至解空间树的任一结点时,总是先判断该结点是否满足问题的约束条件。如果满足进入该子树,继续按深度优先的策略进行搜索。否则,不去搜索以该结点为根的子树,而是逐层向其祖先结点回溯。
回溯法就是对隐式图的深度优先搜索算法。
如图5-14是四皇后问题的搜索过程
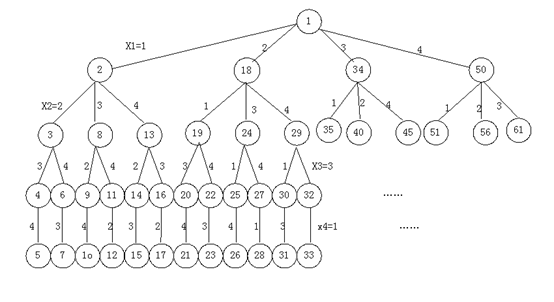
图5-14四皇后问题的解空间树
2.算法设计过程
1)确定问题的解空间
问题的解空间应只至少包含问题的一个解。
2)确定结点的扩展规则
如每个皇后在一行中的不同位置移动,而象棋中的马只能走“日”字等。
3) 搜索解空间
回溯算法从开始结点出发,以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点,同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点,并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时,应往回移动至最近的一个活结点处,并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索,直至找到所要求的解或解空间中已没有活结点时为止。
3.算法框架
1)问题框架
设问题的解是一个n维向量(a1,a2,……,an),约束条件是ai(i=1,2,3……n)之间满足某种条件,记为f(ai)
2)非递归回溯框架
int a[n],i;
初始化数组a[ ];
i=1;
While (i>0(有路可走)) and ([未达到目标]) /还未回溯到头/
{if (i>n) /正在处理第i个元素/
搜索到一个解,输出;
else
{a[i]第一个可能的值;
while (a[i]在不满足约束条件 且 在在搜索空间内)
a[i]下一个可能的值;
if (a[i]在搜索空间内)
{标识占用的资源; i=i+1;} /扩展下一个结点/
else {清理所占的状态空间; i=i-1;}/回溯/
}}
3)递归算法框架
一般情况下用递归函数来实现回溯法比较简单,其中i为搜索深度。
int a[n];
try(int i)
{if (i>n) 输出结果;
else
for( j=下界 ; j<=上界; j++) /枚举i所有可能的路径/
{ if ( f(j) ) /满足限界函数和约束条件/
{ a[i]=j;
…… /其它操作/
try(i+ 1);}
}
回溯前的清理工作(如a[i]置空值等);
}
}
应用1 ——基本的回溯搜索
【例2】马的遍历问题
在n*m的棋盘中,马只能走日字。马从位置(x,y)处出发,把棋盘的每一格都走一次,且只走一次。找出所有路径。
1、问题分析
马是在棋盘的点上行走的,所以这里的棋盘是指行有N条边、列有M条边。而一个马在不出边界的情况下有八个方向可以行走,如当前坐标为(x,y)则行走后的坐标可以为:
(x+1,y+2) ,( x+1, y-2),( x+2, y+1),
( x+2, y-1),(x-1, y -2),(x -1, y+2),
( x -2, y -1),( x -2, y+1)
2、算法设计
搜索空间是整个n*m个棋盘上的点。约束条件是不出边界且每个点只经过一次。结点的扩展规则如问题分析中所述。
搜索过程是从任一点(x,y)出发,按深度优先的原则,从八个方向中尝试一个可以走的点,直到走过棋盘上所有n*m个点。用递归算法易实现此过程。
注意问题要求找出全部可能的解,就要注意回溯过程的清理现场工作,也就是置当前位置为未经过。
3、数据结构设计
1)用一个变量dep记录递归深度,也就是走过的点数,当dep=n*m时,找到一组解。
2)用n*m的二维数组记录马行走的过程,初始值为0表示未经过。搜索完毕后,起点存储的是“1”,终点存储的是 “n*m”。
4、算法
int n=5 , m=4, dep , i, x , y , count;
int fx[8]={1,2,2,1,-1,-2,-2,-1} ,
fy[8]={2,1,-1,-2,-2,-1,1,2} , a[n][m];
main( )
{count=0; dep=1;
print('input x,y'); input(x,y);
if (y>n or x>m or x<1 or y<1)
{ print('x,y error!'); return;}
for(i=1;i<=;i++) for(j=1;j<=;j++) a[i][j]=0;
a[x][y]=1;
find(x,y,2);
if (count=0 ) print(“No answer!”);
else print(“count=!”,count);
}
find(int y,int x,int dep)
{int i , xx , yy ;
for i=1 to 8 do /加上方向增量,形成新的坐标/
{xx=x+fx[i]; yy=y+fy[i];
if (check(xx,yy)=1) /判断新坐标是否出界,是否已走过?/
{a[xx,yy]=dep; /走向新的坐标/
if (dep=n*m)
output( );
else
find(xx,yy,dep+1); /从新坐标出发,递归下一层/
a[xx,yy]=0; /回溯,恢复未走标志/
}
}
}
output( )
{ count=count+1;
print(“换行符”);
print('count=',count);
for y=1 to n do
{print(“换行符”);
for x=1 to m do
print(a[y,x]:3);
}
}
【例3】素数环问题
把从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。
1、算法设计
尝试搜索从1开始,每个空位有2——20共19种可能,约束条件就是填进去的数满足:与前面的数不相同;与前面相邻数据的和是一个素数。第20个数还要判断和第1个数的和是否素数。
2、算法
main()
{ int a[20],k;
for (k=1;k<=20;k++)
a[k]=0;
a[1]=1;
try(2);
}
try(int i)
{ int k
for (k=2;k<=20;k++)
if (check1(k,i)=1 and check3(k,i)=1 )
{ a[i]=k;
if (i=20)
output( );
else
{try(i+1);
a[i]=0;}
}
}
check1(int j,int i)
{ int k;
for (k=1;k<=i-1;k++)
if (a[k]=j ) return(0);
return(1);
}
check2(int x)
{ int k,n;
n= sqrt(x);
for (k=2;k<=n;k++)
if (x mod k=0 ) return(0);
return(1);
}
check3(int j,int i)
{ if (i<20) return(check2(j+a[i-1]));
else
return(check2(j+a[i-1]) and check2(j+a[1]));
}
output( )
{ int k;
for (k=1;k<=20;k++)
print(a[k]);
print(“换行符”);
}
3、算法说明
这个算法中也要注意在回溯前要“清理现场”,也就是置a[i]为0。
【例4】找n个数中r个数的组合。
1、算法设计 先分析数据的特点,以n=5,r=3为例
在数组a中: a[1] a[2] a[3]
5 4 3
5 4 2
5 4 1
5 3 2
5 3 1
5 2 1
4 3 2
4 3 1
4 2 1
3 2 1
分析数据的特点,搜索时依次对数组(一维向量)元素a[1]、a[2]、a[3]进行尝试,
a[ri] i1——i2
a[1]尝试范围5——3
a[2]尝试范围4——2
a[3]尝试范围3——1
且有这样的规律:“后一个元素至少比前一个数小1”,ri+i2均为4。
归纳为一般情况:
a[1]尝试范围n——r,a[2]尝试范围n-1——r-1,……,a[r]尝试范围r——1.
由此,搜索过程中的约束条件为ri+a[ri]>=r+1,若ri+a[ri]<r就要回溯到元素a[ri-1]搜索,特别地a[r]=1时,回溯到元素a[r-1]搜索。
2、算法
main( );
{ int n,r,a[20] ;
print(“n,r=”);
input(n,r);
if (r>n)
print(“Input n,r error!”);
else
{a[0]=r;
comb(n,r);} /调用递归过程/
}
comb2(int n,int r,int a[])
{int i,ri; ri=1; a[1]=n;
while(a[1]<>r-1)
if (ri<>r) /没有搜索到底/
if (ri+a[ri]>=r+1){a[ri+1]=a[ri]-1; ri=ri+1;}
else {ri=ri-1; a[ri]=a[ri]-1;} /回溯/
else
{for (j=1;j<=r;j++) print(a[j]);
print(“换行符”); /输出组合数/
if (a[r]=1) {ri=ri-1;a[ri]=a[ri]-1;} /回溯/
else a[ri]=a[ri]-1; /搜索到下一个数/
}
}
应用2——排列及排列树的回溯搜索
【例5】输出自然数1到n所有不重复的排列,即n的全排列
1、算法设计
n的全排列是一组n元一维向量:(x1,x2,x3,……,xn),搜索空间是:1≤xi≤n i=1,2,3,……n,约束条件很简单,xi互不相同。
这里我们采用第三章“3.2.3 利用数组记录状态信息”的技巧,设置n个元素的数组d,其中的n个元素用来记录数据1——n的使用情况,已使用置1,未使用置0。
2、算法
main( )
{ int j,n,
print(‘Input n=’ ‘);
input(n);
for(j=1;j<=n;j++)
d[j]=0;
try(1);
}
try(int k)
{ int j;
for(j=1;j<=n;j++)
{if (d[j]=0) {a[k]=j; d[j]=1;}
else continue;
if (k<n)
try(k+1);
else
{p=p+1; output(k);}
d[a[k]]=0;
}
}
output( )
{ int j;
print(p,”:”)
for(j=1;j<=n;j++)
print(a[j]);
print(“换行符”);
}
3、算法说明:变量p记录排列的组数,k为当前处理的第k个元素
4、算法分析
全排列问题的复杂度为O(nn),不是一个好的算法。因此不可能用它的结果去搜索排列树。
【例6】全排列算法另一解法——搜索排列树的算法框架
1、算法设计
根据全排列的概念,定义数组初始值为(1,2,3,4,……,n),这是全排列中的一种,然后通过数据间的交换,则可产生所有的不同排列。
2、算法
int a[100],n,s=0;
main( )
{ int i,;
input(n);
for(i=1;i<=n;i++)
a[i]=i;
try(1);
print(“换行符”,“s=”,s);
}
try(int t)
{ int j;
if (t>n)
{output( );}
else
for(j=t;j<=n;j++)
{swap(t,j);
try(t+1);
swap(t,j); /回溯时,恢复原来的排列/
}
}
output( )
{ int j;
printf("\n");
for( j=1;j<=n;j++) printf(" mod d",a[j]);
s=s+1;
}
swap(int t1,int t2)
{ int t;
t=a[t1];
a[t1]= a[t2];
a[t2]=t;
}
3、算法说明
1)有的读者可能会想try( )函数中,不应该出现自身之间的交换,for循环是否应该改为for(j=t+1;j<=n;j++)?回答是否定的。当n=3时,算法的输出是:123,132,213,231,321,312。123的输出说明第一次到达叶结点是不经过数据交换的,而132的排列也是1不进行交换的结果。
2)for循环体中的第二个swap( )调用,是用来恢复原顺序的。为什么要有如此操作呢?还是通过实例进行说明,排列“213”是由“123”进行1,2交换等到的所以在回溯时要将“132” 恢复为“123”。
4、算法分析
全排列算法的复杂度为O(n!), 其结果可以为搜索排列树所用。
【例7】按排列树回溯搜索解决八皇后问题
1、算法设计
利用例6“枚举”所有1-n的排列,从中选出满足约束条件的解来。这时的约束条件只有不在同一对角线,而不需要不同列的约束了。和例1的算法3一样,我们用数组c,d记录每个对角线的占用情况。
2、算法
int a[100],n,s=0,c[20],d[20];
main( )
{ int i;
input(n);
for(i=1;i<=n;i++)
a[i]=i;
for (i=1;i<=n;i++)
{ c[i]=0;
c[n+i]=0;
d[i]=0;
d[n+i]=0;}
try(1);
print("s=",s);
}
try(int t)
{ int j;
if (t>n)
{output( );}
else
for(j=t;j<=n;j++)
{ swap(t,j);
if (c[t+a[t]]=0 and d[t-a[t]+n]=0)
{ c[t+a[t]]=1; d[t-a[t]+n]=1;
try(t+1);
c[t+a[t]]=0; d[t-a[t]+n]=0;}
swap(t,j);
}
}
output( )
{ int j;
print("换行符");
for( j=1;j<=n;j++) print(a[j]);
s=s+1;
}
swap(int t1,int t2)
{ int t;
t=a[t1];
a[t1]= a[t2];
a[t2]=t;
}
应用3——最优化问题的回溯搜索
【例8】一个有趣的高精度数据
构造一个尽可能大的数,使其从高到低前一位能被1整除,前2位能被2整除,……,前n位能被n整除。
1、数学模型
记高精度数据为a1 a2……an,题目很明确有两个要求:
1)a1整除1且
(a1*10+a2)整除2且……
(a1*10n-1+a210n-2+……+an) 整除n;
2)求最大的这样的数。
2、算法设计
此数只能用从高位到低位逐位尝试失败回溯的算法策略求解,生成的高精度数据用数组的从高位到低位存储,1号元素开始存储最高位。此数的大小无法估计不妨为数组开辟100个空间。
算法中数组A为当前求解的高精度数据的暂存处,数组B为当前最大的满足条件的数。
算法的首位A[1]从1开始枚举。以后各位从0开始枚举。所以求解出的满足条件的数据之间只需要比较位数就能确定大小。n 为当前满足条件的最大数据的位数,当i>=n就认为找到了更大的解,i>n不必解释位数多数据一定大;i=n时,由于尝试是由小到大进行的,位数相等时后来满足条件的菀欢ū惹懊娴拇蟆
3、算法
main( )
{ int A[101],B[101]; int i,j,k,n,r;
A[1]=1;
for(i=2;i<=100;i++) /置初值:首位为1 其余为0/
A[i]=0;
n=1; i=1;
while(A[1]<=9)
{if (i>=n) /发现有更大的满足条件的高精度数据/
{n=i; /转存到数组B中/
for (k=1;k<=n;k++)
B[k]=A[k];
}
i=i+1;r=0;
for(j=1;j<=i;j++) /检查第i位是否满足条件/
{r=r*10+A[j]; r=r mod i;}
if(r<>0) /若不满足条件/
{A[i]=A[i]+i-r ; /第i位可能的解/
while (A[i]>9 and i>1) /搜索完第i位的解,回
溯到前一位/
{A[i]=0; i=i-1; A[i]=A[i]+i;}
}
}
}
4、算法说明
1)从A[1]=1开始,每增加一位A[i](初值为0)先计算r=(A[1]*10i-1+A[2]*10i-2+……+A[i]),再测试r=r mod i是否为0。
2)r=0表示增加第i位后,满足条件,与原有满足条件的数(存在数组B中)比较,若前者大,则更新后者(数组B),继续增加下一位。
3)r≠0表示增加i位后不满足整除条件,接下来算法中并不是继续尝试A[i]= A[i]+1,而是继续尝试A[i]= A[i]+i-r,因为若A[i]= A[i]+i-r<=9时,(A[1]*10i-1+A[2]*10i-2+……+A[i]杛+i) mod i肯定为0,这样可减少尝试次数。如:17除5余2,15-2+5肯定能被5整除。
4)同理,当A[i] -r +i>9时,要进位也不能算满足条件。这时,只能将此位恢复初值0且回退到前一位(i=i-1)尝试A[i]= A[i] +i……。这正是最后一个while循环所做的工作。
5)当回溯到i=1时,A[1]加1开始尝试首位为2的情况,最后直到将A[1]=9的情况尝试完毕,算法结束。
【例9】流水作业车间调度
n个作业要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工,然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。流水作业调度问题要求确定这n个作业的最优加工顺序,使得从第一个作业在机器M1上开始加工,到最后一个作业在机器M2上加工完成所需的时间最少。作业在机器M1、M2的加工顺序相同。
1、算法设计
1)问题的解空间是一棵排列树,简单的解决方法就是在搜索排列树的同时,不断更新最优解,最后找到问题的解。算法框架和例6完全相同,用数组x(初值为1,2,3,……,n)模拟不同的排列,在不同排列下计算各种排列下的加工耗时情况。
2)机器M1进行顺序加工,其加工f1时间是固定的,f1[i]= f1[i-1]+a[x[i]]。机器M2则有空闲(图5-19(1))或积压(图5-19(2))的情况,总加工时间f2,当机器M2空闲时,f2[i]=f1+ b[x[i]];当机器M2有积压情况出现时,f2[i]= f2[i-1]+ b[x[i]]。总加工时间就是f2[n]。
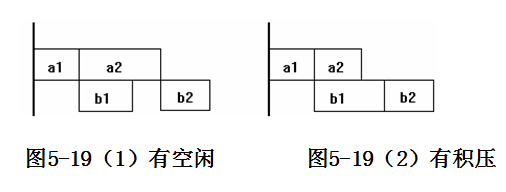
3)一个最优调度应使机器M1没有空闲时间,且机器M2的空闲时间最少。在一般情况下,当作业按在机器M1上由小到大排列后,机器M2的空闲时间较少,当然最少情况一定还与M2上的加工时间有关,所以还需要对解空间进行搜索。排序后可以尽快地找到接近最优的解,再加入下一步限界操作就能加速搜索速度。
4)经过以上排序后,在自然数列的排列下,就是一个接近最优的解。因此,在以后的搜索过程中,一当某一排列的前面几步的加工时间已经大于当前的最小值,就无需进行进一步的搜索计算,从而可以提高算法效率。
2、数据结构设计
1)用二维数组job[100][2]存储作业在M1、M2上的加工时间。
2)由于f1在计算中,只需要当前值,所以用变量存储即可;而f2在计算中,还依赖前一个作业的数据,所以有必要用数组存储。
3)考虑到回溯过程的需要,用变量f存储当前加工所需要的全部时间。
3、算法
int job[100][2],x[100],n,f1=0,f=0,f2[100]=0;
main( )
{ int j;
input(n);
for(i=1;i<=2;i++)
for(j=1;j<=n;j++)
input(job[j][i]);
try( );
}
try(int i)
{ int j;
if (i=n+1)
{for(j=1;j<=n;j++)
bestx[j]=x[j];
bestf=f;
}
else
for(j=1;j<=n;j++)
{ f1= f1+ job[x[j]][1];
if (f2[i-1]>f1) f2[i]= f2[i-1]+job[x[j]][2];
else f2[i]= f1+job[x[j]][2];
f=f+f2[i];
if (f<bestf)
{ swap(x[i],x[j]); try(i+1);
swap(x[i],x[j]);}
f1= f1-job[x[j]][1];
f=f-f2[i];
}
}
解空间为排列树的最优化类问题,都可以依此算法解决。而对于解空间为子集树的最优化类问题,类似本节例题1、2、3枚举元素的选取或不选取两种情况进行搜索就能找出最优解,同时也可以加入相应的限界策略。



