16图的搜索算法之先深
深度优先搜索
深度优先遍历首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点均已被访问为止。
若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。
深度搜索与广度搜索的相近，最终都要扩展一个结点的所有子结点.
区别在于对扩展结点过程，深度搜索扩展的是E-结点的邻接结点中的一个，并将其作为新的E-结点继续扩展，当前E-结点仍为活结点，待搜索完其子结点后，回溯到该结点扩展它的其它未搜索的邻接结点。而广度搜索，则是扩展E-结点的所有邻接结点，E-结点就成为一个死结点。
1．算法的基本思路
算法设计的基本步骤为：
1）确定图的存储方式；
2）遍历过程中的操作，其中包括为输出问题解而进行的存储操作；
3）输出问题的结论。
4）一般在回溯前的应该将结点状态恢复为原始状态，特别是在有多解需求的问题中。
2．算法框架
1）用邻接表存储图的搜索算法
graph head[100]；
dfs(int k) / head图的顶点数组/
{ edgenode *ptr / ptr图的边表指针/
visited[k]=1; /* 记录已遍历过 */
print(“访问 ”,k); /* 印出遍历顶点值 */
ptr=head[k].firstedge; /* 顶点的第一个邻接点 */
while ( ptr <> NULL ) /* 遍历至链表尾 */
{if ( visited[ptr->vertex]=0) /* 如过没遍历过 */
dfs(ptr->vertex); /* 递归遍历 */
ptr = ptr->nextnode; } /* 下一个顶点 */
}
算法分析：n图中有 n 个顶点，e 条边。扫描边的时间为O(e)。遍历图的时间复杂性为O(n+e)。
2）用邻接矩阵存储图的搜索算法
- graph g[100][100],int n；
- dfsm(int k)
{int j；
print(“访问 ”,k);
visited[k]=1；
for(j=1；j<=n；j++) //依次搜索vk的邻接点
if(g[k][j]=1 and visited[j]=0)
dfsm(g,j)
//(vk，vj)∈E，且vj未访问过，故vj为新出发点
}
算法分析：查找每一个顶点的所有的边，所需时间为O(n)，遍历图中所有的顶点所需的时间为O(n2)。
【例1】 走迷宫问题
1、算法设计：深度优先搜索，就是一直向着可通行的下一个方格行进，直到搜索到出口就找到一个解。若行不通时，则返回上一个方格，继续搜索其它方向。
2、数据结构设计：
还是用迷宫本身的存储空间除了记录走过的信息，还要标识是否可行：
maze[i][j]=3 标识走过的方格 ；
maze[i][j]=2 标识走入死胡同的方格，
这样，最后存储为“3”的方格为可行的方格。而当一个方格四个方向都搜索完还没有走到出口，说明该方格或无路可走或只能走入了“死胡同”。
3、算法
int maze[8][8]={{0,0,0,0,0,0,0,0},
{0,11,1,1,0,1,0},{0,0,0,0,1,0,1,0},
{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},
{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0},
{0,1,1,1,1,1,1,0}};fx[4]={1,-1,0,0},
fy[4]={0,0,-1,1}; int i,j,k,total;
main( )
{ int total=0;
maze[1][1]=3; /入口坐标设置已走标志/
search(1,1);
print(“Total is”,total); /统计总步数/
}
search(int i, int j)
{int k,newi,newj;
for(k=1;k<=4;k++) /搜索可达的方格/
if(check(i,j,k)=1)
{newi=i+fx[k]; newj=j+fy[k];
maze[newi][newj]=3; /来到新位置后,设置已走过标志/
if (newi=8 and newj=8) /到出口则输出,否则下一步递归/
Out( );
else search(newi,newj);
}
maze[i][j]=2; /某一方格只能走入死胡同/
}
Out( )
{ int i,j;
for( i=1;i<=8;i++)
{ print(“换行符”);
for(j=1;j<=8;j++)
if（maze[i][j]=3）
{print(“V”);
total++;} /统计总步数/
else
print(“*”);
}
}
check(int i,int j,int k)
{int flag=1;
i= i+fx[k]; j= j +fy[k];
if(i<1 or i>8 or j<1 or j>8) /是否在迷宫内/
flag=0;
else
if(maze[i][j]<>0) /是否可行/
flag=0;
return(flag);
}
4、算法说明：
1）和广度优先算法一样每个方格有四个方向可以进行搜索，这样一点结点（方格）就可多次成为“活结点”，而在广度优先算法一点结点（方格）就可一次成为“活结点”，一出队就成了死结点。
2）用广度优先算法，搜索出的是一条最短的路径，而用深度优先搜索则只能找出一条可行的路径，而不能保证是最短的路径。
3）在空间效率上二者相近。都需要辅助空间。
【例2】 有如图1所示的七巧板，试编写一源程序如下，使用至多四种不同颜色对七巧板进行涂色(每块涂一种颜色)，要求相邻区域的颜色互不相同，打印输出所有可能的涂色方案。
1.问题分析:
为了让算法能识别不同区域间的相邻关 系，我们把七巧板上每一个区域看成一个顶点若两个区域相邻，则相应的顶点间用一条边相连，这样该问题就转化为图一个图的搜索问题了。
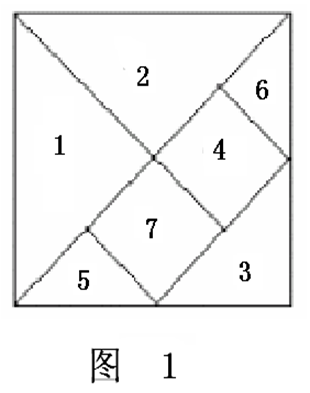
2、算法设计:
按顺序分别对１号、２号、......、７号区域进行试探性涂色，用１、２、３、４号代表４种颜色。
则涂色过程如下：
1)对某一区域涂上与其相邻区域不同的颜色。
2)若使用４种颜色进行涂色均不能满足要求，则回溯一步，更改前一区域的颜色。
3）转步骤１继续涂色，直到全部区域全部涂色为止，输出结果。
已经有研究证明，对任意的平面图至少存在一种四色涂色法。
3、数据采用的存储结构：邻接矩阵存储
0 1 0 0 1 0 1
1 0 0 1 0 1 0
0 0 0 0 0 1 1
0 1 0 0 0 1 1
1 0 0 0 0 0 1
0 1 1 1 0 0 0
1 0 1 1 1 0 0
4、算法如下:
int data[7][7],n,color[7],total;
main( )
{ int i,j;
for(i=1;i<=7;i++)
for(j=1;j<=7;j++)
input(data[i][j]);
for(j=1;j<=7;j++)
color[j]=0;
total=0;
try(1);
print(“换行符,Total=”,total);
}
try(int s)
{ int i,;
if (s>7)
output( );
else
for(i=1;i<=4;i++)
{ color[s]=i;
if （colorsame(s)=0）
try(s+1);
}
}
output( )
{ int i,;
print(“换行符，serial number：”,total);
for( i=1;i<= n;i=i=1)
print(color[i]);
total=total+1;
}
colorsame(int s) /判断相邻点是否同色/
{ int i,flag;
flag=0;
for(i=1;i<=s-1;i++)
if (data[i][s]=1 and color[i]=color[s])
flag=1;
return(flag)
}
【例3】关结点的判断及消除
1．网络安全相关的概念
在一个无向连通图G中，当且仅当删去G中的顶点v及所有依附于v的所有边后，可将图分割成两个以上的连通分量，则称v为图G的关结点，关结点亦称为割点。
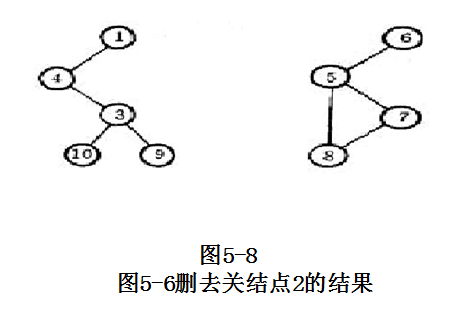
一个表示通信网络的图的连通度越高，其系统越可靠。
网络安全比较低级的要求就是重连通图。在重连通图上，任何一对顶点之间至少存在有两条路径，在删除某个顶点及与该顶点相关联的边时，也不破坏图的连通性。即“如果无向连通图G根本不包含关结点，则称G为重连通图”。
不是所有的无向连通图都是重连通图。
2．连通图G的关结点的判别
算法设计：连通图中关结点的判别方法如下：
1)从图的某一个顶点开始深度优先遍历图，得到深度优先生成树
2)用开始遍历的顶点作为生成树地根，
一、根 顶点是图的关结点的充要条件是，根至少有两个子 女。
二、其余顶点u是图的关结点的充要条件是，该顶点u至少有一个子女w，从该子女出发不可能通过该子女顶点w和该子女w的子孙顶点，以及一条回 边所组成的路径到达u的祖先，不具有可行性。
三、特别的，叶结点不是关结点。
例：图中，每个结点的外面都有一个数，它表示按深度优先检索算法访问这个结点的次序，这个数叫做该结点的深度优先数（DFN）。
例如：DFN(1)=1，DFN(4)=2，DFN(8)=10等等。
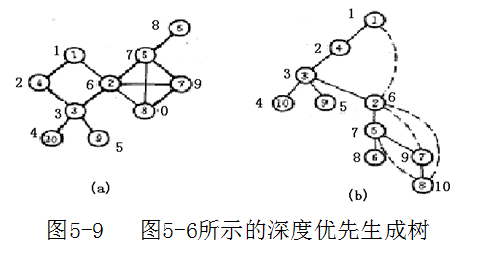
图5-9 (b)中的实线边构成这个深度优先生成树，这些边是递归遍历顶点的路径，叫做树边,虚线边为回边。
定义：
L(u)=Min DFN[u],low[w],DFN[k] w是u在DFS生成树上的孩子结点; k是u在DFS生成树上由回边联结的祖先节点；(u,w)∈实边;(u,k)∈虚边,显然，L(u)是u通过一条子孙路径且至多后随一条逆边所可能到达的最低深度优先数。如果u不是根，那么当且仅当u有一个使得L(w)=DFN(u)的儿子w时，u是一个关结点。
对于图5-8（b）所示的生成树，各结点的最低深度优先数是：L(1:10)=(1,1,1,1,6,8,6,6,5,4)。
由此，结点3是关结点，因为它的儿子结点10有L(10)=4>DFN(3)=3。同理，结点2、5也是关结点.
按后根次序访问深度优先生成树的结点，可以很容易地算出L（U）。于是，为了确定图G的关结点,必须既完成对G的深度优先检索，产生G的深度优先生成树T，又要按后根次序访问树T的结点。
算法ART——计算DFN和L的算法如下：
int DFN[n]，L[n]，num，n
ART（u，v） //u是深度优先检索的开始结点。在深度优先生成树中，
u若有父亲，那末v就是它的父亲。假设数组DFN是全程量，并将其初始化为0。num是全程变量，被初始化为 1。n是 G的结点数
算法如下：
int DFN[n]，L[n]，num=1，n；
TRY（u，v）
{DFN[u]=num；L[u]=num；num=num＋1；
while （每个邻接于u的结点 w ）
if （DFN（w）=0）
{TRY（w，u）；
if(L（u）>L（w）L（u）=L（w）；}
else if （w<>v）
if (L（u）>DFN（w）)
L（u）= DFN（w）；
}
算法说明：
算法ART实现了对图G的深度优先检索；在检索期间，对每个新访问的结点赋予深度优先数；同时对这棵树中每个结点的L（i）值也进行计算。
如果连通图G有n个结点e条边，且G由邻接表表示，那末ART的计算时间为O（n＋e）。识别关结点的总时间不超过O（n＋e）。
3．非重连通图的加边策略
G‘=( V’, E‘ )是G的最大重连通子图，指的是G中再没有这样的重连通子图G’‘=( V’‘, E’‘ )存在，使得V’V‘’且E‘E’‘。
最大重连通子图称为重连通分图
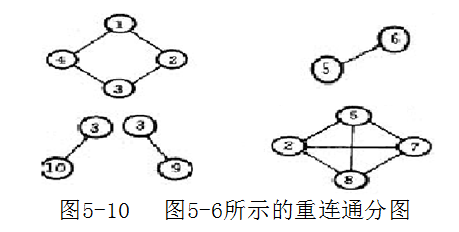
两个重连通分图至多有一个公共结点，且这个结点就是割点。因而可以推出任何一条边不可能同时出现在两个不同的重连通分图中（因为这需要两个公共结点）。选取两个重连通分图中不同的结点连结为边，则生成的新图为重连通的。多个重连通分图的情况依此类推。
使用这个方法将图5-6变成重连通图，需要对应于关结点3增加边（4，10）和（10，9）；对应关结点2增加边（1，5）；对应关结点5增加（6，7），结果如图5-11。
