14图的基本概念
图是一种限止最少的数据结构,因此更接近现实,实际问题中很多数据关系都可以抽象成图,相关问题则可利用图的基本算法进行求解,很早就有专门研究图的是一门数学学科“图论”;其中的计算问题包括图的搜索、路径问题、连通性问题、可平面性检验、着色问题、网络优化等。图论中的著名算法有:求最小生成树的Kruskal算法、求最短路径的Dijkstra算法和Floyd算法、求二部图最大匹配(指派问题)的匈牙利算法、求一般图最大匹配的Edmonds“花”算法、求网络最大流和最小割的算法等。
图及其术语
1.显式图与隐式图
在路径问题、连通性问题、可平面性检验、着色问题和网络优化等问题中,图的结构是显式给出的,包括图中的顶点、边及权重,这类图我们称为显式图,也就是一般意义上的图。
隐式图是由问题的初始结点,为了求解或求证问题,根据题目的规则(一般是由题目的意思隐含给出的),也就是生成子结点的约束条件,逐步扩展结点,直到得到目标结点为止的一个隐式的图。
2.显式图的常用术语
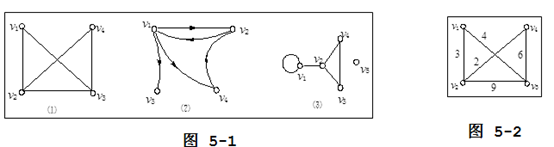
如图5-1所示的 ⑴, ⑵, ⑶均为显式图 (Graph)。图中的这些点(v1,v2,…,vn)被称为顶点 (vertex)或结点,连接顶点的曲线或直线称为边 (edge)。
通常将这种由若干个顶点以及连接某些顶点的边所组成的图形称为图,顶点通常被称作是图中的数据元素 .
带权图:j即图5 -2给图 5-1中各图的边上附加一个代表性数据 (比如表示长度、流量或其他 ),则称其为带权图 。
环 (cycle):图5-1中 ⑶图中的 v 1点本身也有边相连,这种边称为环。
有限图:顶点与边数均为有限的图,如图 5-1中的三个图均属于有限图。
简单图:没有环且每两个顶点间最多只有一条边相连的图,如图 5-1中的 ⑴图。
邻接与关联:当( v 1, v 2) ∈E,或 <v 1, v 2 >∈E,即 v 1, v 2间有边相连时,则称 v 1和 v 2是相邻的,它们互为邻接点( adjacent),同时称( v 1, v 2)或 <v 1, v 2 >是与顶点 v 1、 v 2相关联的边。
顶点的度数 (degree):从该顶点引出的边的条数,即与该顶点相关联的边的数目,简称度。
入度( indegree):有向图中把以顶点 v为终点的边的条数称为是顶点 v的入度。
出度( outdegree):有向图中把以顶点 v为起点的边的条数称为是顶点 v的出度。
终端顶点:有向图中把出度为 0的顶点称为终端顶点,如图 5-1中 ⑵图的 v 3。
路径与路长:在图 G=( V, E)中,如果存在由不同的边 (v i0, v i1 ), (v i1, v i2 ), …, (v in-1, v in )或是 <v i0, v i1 >, <vi 1, v i 2>, …, < v in-1, v in >)组成的序列,则称顶点 v i0, v in是连通的,顶点序列( v i0, v i1, v i2, …, v in)是从顶点 v i0到顶点 v in的一条道路。路长是道路上边的数目, v i0到 v in的这条道路上的路长为 n。
连通图:对于图中任意两个顶点 v i、 v j ∈V, v i、 v j之间有道路相连,则称该图为连通图。如 5-1中的 ⑴图。
网络:带权的连通图,如图 5-2所示。
3.隐式图术语
1)子集树
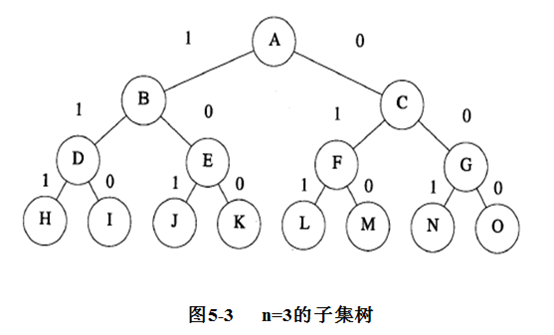
当要求解的问题需要是在n 个元素的子集中进行搜索,其搜索空间树被称作子集树(subset tree)。这n个元素都有在子集中或被选取记为1,不在子集中或被舍去记为0,这样搜索空间为:
(0,0,……,0,0),(0,0,……,0,1),
(0,0,……,1,0),(0,0,……,1,1),
……(1,1,……,1,1)。
共2n 个状态。若表示为树形结构就是一棵有2n个叶结点的二叉树,对树中所有分支进行遍历的算法都必须耗时O(2n)。
2)排列树
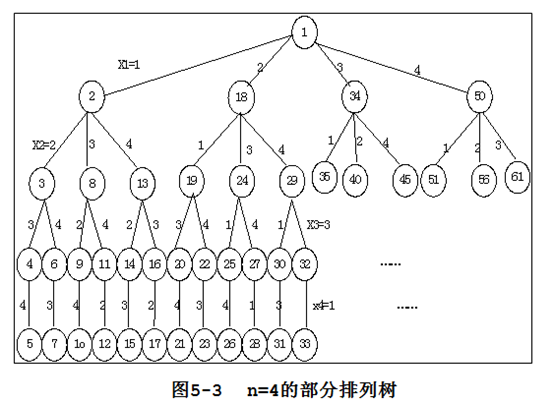
当要求解的问题需要在n 元素的排列中搜索问题的解时,解空间树被称作排列树(permutation tree)。
搜索空间为:
(1,2,3,……,n-1,n), (2,1,3,……,n-1,n), (2,3,1,……,n-1,n),(2,3,4,1,……,n-1,n),(n,n-1,……,3,2,1)
第一个元素有n 种选择,第二个元素有n-1种选择,第三个元素有n-2种选择,……,第n个元素有1种选择,共计n!个状态。若表示为树形就是一个n度树,这样的树有n! 个叶结点,所以每一个遍历树中所有节点的算法都必须耗时O(n! )
4.图的存储
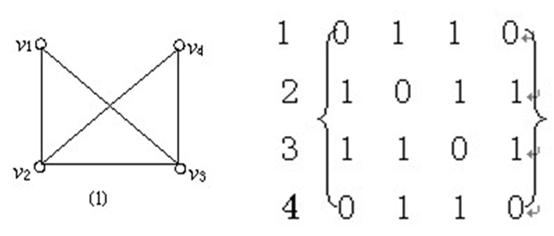
1)邻接矩阵法
邻接矩阵是表示顶点之间相邻关系的矩阵,
设G=(V,E)是具有n个顶点的图,则G的邻接矩阵可定义为:
A[i,j]=1, 若(Vi,Vj)或<Vi,Vj>是E(G)中的边。
A[i,j]=0, 若 (Vi,Vj)或<Vi,Vj>不是E(G)中的边。
若G是网络,则邻接矩阵可定义为:
A[i,j]=Wij 若(Vi,Vj)或<Vi,Vj>属于E(G);
A[i,j]=0或∞ 若(Vi,Vj)或<Vi,Vj> 不属于E(G);
其中,Wij表示边上的权值,∞表示一个计算机允许的,大于所有边上权值的数;
2)邻接表
对于图G中的每个结点Vi, 把所有邻接于Vi的顶点Vj链成一个单链表,这个单链表就称为顶点Vi的邻接表。
邻接表由边表和顶点两部分组成。
边表为一个单链表,每个表结点均有两个域:
① 邻接点域adjvex,存放与vi相邻接的顶点vj的序号j。
② 链域next,将邻接表的所有表结点链在一起。
顶点表为一数组a,每个元素均有两个域:
①顶点域vertex,存放顶点vi的信息
② 指针域firstedge, vi的边表的头指针。
对于无向图来说,Vi的邻接表中每个表结点都对应于与Vi相关联的一条边,
对于有向图来说,Vi的邻接表中每个表结点对应于Vi为始点射出的一条边。

图搜索及其术语
1.穷举搜索与启发式搜索
穷举搜索是对图的最基本的搜索算法,是蛮力策略的一种表现形式。即不考虑给定问题的特有性质,按事先定好的顺序,依次运用规则,盲目搜索的方法。
启发式搜索是利用一些启发信息,提前判断出先搜索哪些状态可能尽快找到问题的解或某些情况不可能取到最优解,从而可以提前舍弃对这些状态的尝试。即考虑给定问题的特有性质,选用合适的细则,提高搜索的效率。
2.相关概念和术语
问题状态:树中的每一个结点确定所求解问题的一个问题状态。
状态空间:由根结点到其它结点的所有路径(分支),就确定了这个问题的状态空间。
解状态:是这样一些问题状态S,对于这些问题状态,由根到S 的那条路径确定了这解空间中的一个元组。
答案状态:是这样的一些解状态S,对于这些解状态而言,由根到S的这条路径确定了这问题的一个解
状态空间树:解空间的树结构又称隐式图。
活结点:如果已生成一个结点而它的所有儿子结点还没有全部生成,则这个结点叫做活结点。
E-结点:当前正在生成其儿子结点的活结点叫E-结点(正扩展的结点)。
死结点 :不再进一步扩展或者其儿子结点已全部生成的生成结点就是死结点 。



