11算法策略之动态规划
动态规划
在动态规划算法策略中,体现在它的决策不是线性的而是全面考虑不同的情况分别进行决策, 并通过多阶段决策来最终解决问题。在各个阶段采取决策后, 会不断决策出新的数据,直到找到最优解.每次决策依赖于当前状态, 又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义。所以,这种多阶段决策最优化的解决问题的过程称为动态规划。
【例1】数塔问题
有形如图4-11所示的一个数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的数值和最大。
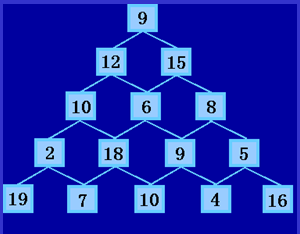
图4-11
问题分析
这个问题用贪婪算法有可能会找不到真正的最大和。以图4-11为例就是如此。用贪婪的策略,则路径和分别为:
9+15+8+9+10=51 (自上而下),
19+2+10+12+9=52(自下而上)。
都得不到最优解,真正的最大和是:
9+12+10+18+10=59。
在知道数塔的全貌的前提下,可以用枚举法或搜索算法来完成。
算法设计
动态规划设计过程如下:
1.阶段划分:
第一步对于第五层的数据,我们做如下五次决策:
对经过第四层2的路径选择第五层的19,
对经过第四层18的路径选择第五层的10,
对经过第四层9的路径也选择第五层的10,
对经过第四层5的路径选择第五层的16。
以上的决策结果将五阶数塔问题变为4阶子问题,递推出第四层与第五层的和为:
21(2+19),28(18+10),19(9+10),21(5+16)。
用同样的方法还可以将4阶数塔问题,变为3阶数塔问题。…… 最后得到的1阶数塔问题,就是整个问题的最优解。
2.存储、求解:
1) 原始信息存储
原始信息有层数和数塔中的数据,层数用一个整型
变量n存储,数塔中的数据用二维数组data,存储成如
下的下三角阵:
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16
2) 动态规划过程存储
必需用二维数组a存储各阶段的决策结果。二维数组a的存储内容如下:
d[n][j]=data[n][j] j=1,2,……,n;
i=n-1,n-2,……1,j=1,2,……,i;时
d[i][j]=max(d[i+1][j],d[i+1][j+1])+data[i][j]
最后a[1][1]存储的就是问题的结果。
3) 最优解路径求解及存储
仅有数组data和数组a可以找到最优解的路径, 但需要自顶向下比较数组data和数组a是可以找到。如图4.5.2求解和输出过程如下:


为了设计简洁的算法,我们最后用三维数组a[50][50][3]存储以上确定的三个数组的信息。
a[50][50][1]代替数组data,
a[50][50][2]代替数组d,
a[50][50][3]记录解路径。
数塔问题的算法
main( )
{ int a[50][50][3],i,j,n;
print( 'please input the number of rows:');
input(n);
for( i=1 ;i<=n;i++)
for j=1 to i do
{ input(a[i][j][1]);
a[i][j][2]=a[i][j][1];
a[i][j][3]=0;}
for (i=n-1 ; i>=1;i--)
for (j=1 ;j>= i ;j++)
if (a[i+1][j][2]>a[i+1][j+1][2])
{ a[i][j][2]=a[i][j][2]+a[i+1][j][2];
a[i][j][3]=0;}
else
{ a[i][j][2]=a[i][j][2]+a[i+1][j+1][2];
a[i][j][3]=1;}
print('max=’,a[1][1][2]);
j=1;
for( i=1 ;i<= n-1;i++)
{ print(a[i][j][1],‘->’);
j=j+a[i][j][3]; }
print (a[n][j][1]);
}
从例子中可以看到:
动态规划=贪婪策略+递推(降阶)+存储递推结果
贪婪策略、递推算法都是在“线性”地解决问题,而动态规划则是全面分阶段地解决问题。可以通俗地说动态规划是“带决策的多阶段、多方位的递推算法”。
1.适合动态规划的问题特征
动态规划算法的问题及决策应该具有三个性质:最优化原理、无后向性、子问题重叠性质。
1) 最优化原理(或称为最佳原则、最优子结构)。
2) 无后向性(无后效性)。
3) 有重叠子问题。
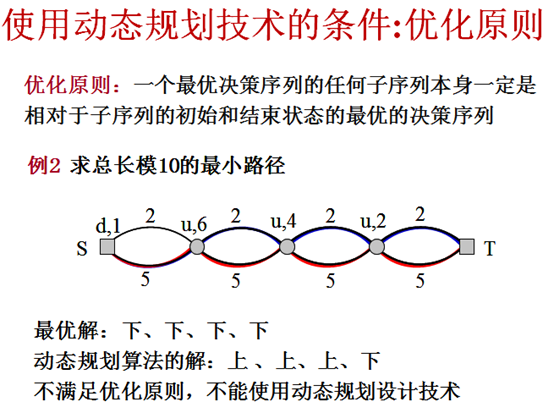
2. 动态规划的基本思想
动态规划方法的基本思想是,把求解的问题分成许多阶段或多个子问题,然后按顺序求解各子问题。最后一个子问题就是初始问题的解。
由于动态规划的问题有重叠子问题的特点,为了减少重复计算,对每一个子问题只解一次,将其不同阶段的不同状态保存在一个二维数组中。
3. 设计动态规划算法的基本步骤
设计一个标准的动态规划算法的步骤:
1) 划分阶段
2) 选择状态
3) 确定决策并写出状态转移方程但是,实际应用当中的简化步骤:
1) 分析最优解的性质,并刻划其结构特征。
2) 递推地定义最优值。
3) 以自底向上的方式或自顶向下的记忆化方法(备忘录法)计算出最优值.
4) 根据计算最优值时得到的信息,构造问题的最优解。
4. 标准动态规划的基本框架
for( j=1 ;j<=m;j=j+1) //第一个阶段
xn[j]=初始值;
for (i=n-1 ; i>=1;i=i-1) //其它n-1个阶段
for (j=1 ;j>=f(i) ;j=j+1)//
f(i)与 i有关的表达式
xi[j]=max(或min){g(xi+1[j1——j2]),……,
g(xi+1[jk——jk+1])};
t=g(x1[j1—j2]); //由最优解求解最优解的方案print(x1[j1]);
for( i=2 ;i<= n-1;i=i+1)
{t=t-xi-1[ji];
for (j=1 ;j>=f(i) ;j=j+1)
if(t= xi[ji]) break;}
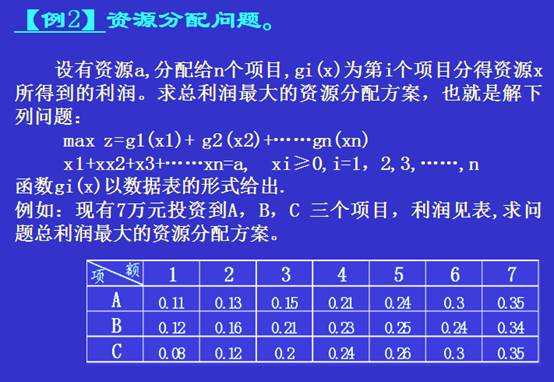
算法设计
1.阶段划分及决策
比较直观的阶段划分就是逐步考虑每一个项目在不同投资额下的利润情况。
3. 数据结构设计:
1) 开辟一维数组q来存储原始数据。
2) 另开辟一维数组f存储当前最大收益情况。
3) 开辟记录中间结果的一维数组数组temp,记录正在计算的最大收益。
4) 开辟二维数组a。
5) 数组gain存储第i个工程投资数的最后结果。
对于一般问题设计算法如下:
main( )
{ int i,j,k,m,n,rest;
int a[100][100],gain[100];
float q[100],f[100],temp[100];
print(“How many item? ”); input (m);
print(“How many money? ”); input (n);
print(“input gain table:”);
for( j=0;j<= n;j++)
{ input(q[j]); f[j]=q[j];}
for( j=0;j<= n;j++)
a[1][j]=j;
for( k=2;k<=m;k++)
{ for( j=0;j<= n;j++)
{ temp[j]=q[j]; input(q[j]); a[k][j]=0;}
for( j=0 ;j<= n;j++)
for( i=0 ;i<=j;i++)
if(f[j-i]+q[i]>temp[j])
{ temp[j]=f[j-i]+q[i]; a[k,j]=i; }
for(j=0;j<= n;j++)
f[j]=temp[j];
}
rest=n;
for(i=m;i>=1;i--)
{ gain[i]=a[i][rest]; rest=rest-gain[i];}
for(i=1;i<=m;i++) print(gain[i],” ”);
print(f[n]);
}
【例3】n个矩阵连乘的问题。
问题分析
多个矩阵连乘运算是满足结合律的。
例:
M1[5*20] * M2[20*50] * M3[50*1] * M4[1*100]分别按
((M1*M2)*M3)*M4,M1*(M2*(M3*M4)),(M1*(M2*M3))*M4
的次序相乘,各需进行 5750, 115000, 1600次乘法。
这个问题要用“动态规划”算法来完成:
首先,从两个矩阵相乘的情况开始;
然后,尝试三个矩阵相乘的情况;
……
最后,等到n个矩阵相乘所用的最少的乘法次数及结合方式。
算法设计
1. 阶段划分
1)初始状态为一个矩阵相乘的计算量为0;
2)第二阶段,计算两个相邻矩阵相乘的计算量, 共n-1组
3)第三阶段,计算两个相邻矩阵相乘的计算量, 共n-2组
4)最后一个阶段,是n个相邻矩阵相乘的计算量,共1组,是问题解。
2. 阶段决策
一般地,计算M1*M2*M3*……*Mn 其中M1,M2,……,Mi分别是
r1*r2,r2*r3,……,ri*ri+1阶矩阵,i=1,2,3,……n。
设mi,j是计算Mi*Mi+1*…Mj的最少乘法次数(1≤i≤j≤n),对
mi,j有公式:
0 当i=j时
ri*ri+1*ri+2 当i=j-1时
min(mi,k+mk+1,j+rirk+1rj+1) i≤k<j 当i<j-1时
以上动态规划方法是按s=0,1,2,3,.,n-1的顺序计算mi,i+s的。
3.记录最佳期方案
用二维矩阵comij(n*n)来存储使mij为最小值时的 k 值。
算法1(递归算法)
int r[100],com[100][100];
main( )
{ int n,i;
print(“How mang matrixes?”); input (n);
peint(“How size every matrixe?”);
for (i=1;i<=n+1;i++) input (r[i]);
print (“The least calculate quantity:”, course (1,n));
for (i=1;i<=n;i++)
{ print(“换行符”);
for (j=1;j<=n;j++)
print(com[i][j]); }
}
int course(int i, int j)
{ int u,t;
if (i=j) {com[i][i]=i; return 0; }
if (i=j-1)
{ com[i][i+1]=i; return( r[i]*r[i+1]*r[i+2]);}
u= course(i,i) + course(i+1,j)+ r[i]*r[i+1]*r[j+1];
com[i][j] = i;
for (int k = i+1; k < j; k++)
{ t = course(i,k) + course(k+1,j)+r[i]*r[k+1]*r[j+1];
if (t<u) { u= t; com[i][j] = k;} }
return u;
}
算法1说明:
以上的递归算法虽然解决了问题,但效率很低,有子问题重叠,n=4时的递归过程如下图:
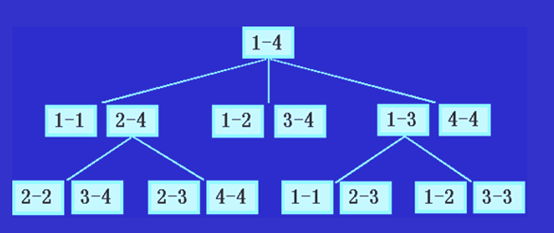
算法2(改进后递归算法)
int m[100][100],com[100][100],r[100];
matrix2( )
{ int n,;
print(“How mang matrixes?”); input (n);
print(“How size every matrixe?”);
for (i=1;i<=n+1;i++) input (r[i]);
for (i=1;i<=n;i++) /初始化化数组com和m。/
for (j=1;j<=n;j++)
{ com[i][j]=0; m[i][j]=0; }
course (1,n);
print (“The least calculate quantity:”m[1][n]);
for (i=1;i<=n;i++)
{ print(“换行符”);
for (j=1;j<=n;j++) print(com[i][j]); }
}
course (int i,int j)
{ if (m[i][j]>0) return m[i][j];
if(i=j) return 0;
if(i=j-1)
{ com[i][i+1]=i; m[i][j]= r[i]*r[i+1]*r[i+2]; return m[i][j]; }
int u= course (i,i)+ course (i+1,j)+r[i]*r[i+1]*r[j+1];
com[i][j]=i ;
for (int k==i+1; k<j;k++)
{ int t= course (i,k)+ course (k+1,j)+r[i]*r[k+1]*r[j+1];
if (t<u) { u=t ; com[i][j]=k; }
}
m[i][j]=u;
return u;
}
算法3(非递归算法)
main( )
{ int n,r[100],m[100][100],com[100][100];
peint(“How mang matrixes?”); input (n);
peint(“How size every matrixe?”);
for (i=1;i<=n+1;i++) input (r[i]);
for (i=1;i<=n;i++) /初始化化数组com和m。/
for (j=1;j<=n;j++) com[i][j]=0;
for (i=1;i<n;i++)
{ m[i][i]=0; \s=0\
m[i][i+1]= r[i]*r[i+1]*r[i+2]; \s=1\
com[i][i+1] = i+1;
}
m[n][n]= 0;
for ( s =2; s<=n-1; s++) /动态规划过程/
for (i=1;i<n-s+1;i++)
{ j=i+s; m[i][j] =m[i][i] +m[i+1][j] + r[i]*r[i+1]*r[j+1];
com[i][j] = i;
for (k=i+1;k<j;k++)
{ t=m[i][k]+m[k+1][j]+ r[i]*r[k+1]*r[j+1];
if (t <m[i][j]) { m[i][j] = t; com[i][j]= k;} }
}
print (“The least calculate quantity:”m[1][n]);
for (i=1;i<=n;i++)
{ print(“换行符”);
for (j=1;j<=n;j++) print(com[i][j]); }
}
输出部分的算法设计
以上算法中关于矩阵相乘的结合方式,只是简单的输出了数组com的内容,不容易直观地被利用,还需要继续进行必要的人工处理,才能真正找到矩阵相乘的结合方式。怎么样更直观、合理地输出结合过程?即算法的输出能使用户直接了解计算矩阵的过程。
首先看一下com数组存储的信息意义,它是一个二维数组,元素com[i][j]存储的是Mi——Mj相乘的组合点k1,也就是说:
Mi*Mi+1*……*Mj是由 Mi*Mi+1*……Mk和Mk+1*……Mj
同样,在数组com中我们也能找到Mi——Mk相乘的组合点k2,Mk+1——Mj相乘的组合点k3,……。
从数组信息中找到了大规模问题与小规模问题的递归关系:
输出算法
记k1=com[1][n],则最后一次运算的结合过程是
M1*……*Mk1和Mk1+1*……*Mn
记k2=com[1][k1],M1*……*Mk1的结合过程是
M1*……*Mk2和Mk2+1*……*Mk1
……
combine(int i, int j)
{ if ( i=j) return;
combine (i, com[i][j]);
combine (com[i][j]+1, j);
print("M",i ,“*M”,com[i][j]);
print(" and M",com[i][j]+1, “*M”,j );
}
小结:
动态规划=贪婪策略+递推(降阶)+存储递推结果
贪婪策略、递推算法都是在“线性”地解决问题,而动态规划则是全面分阶段地解决问题。可以通俗地说动态规划是“带决策的多阶段、多方位的递推算法”。
【例4】求两个字符序列的最长公共字符子序列。
问题分析
若A的长度为n,若B的长度为m,则
A的子序列共有: Cn1+Cn2+ Cn3+……+Cnn=2n-1
B的子序列共有: Cm1+Cm2+ Cm3+……+Cmm=2m-1
如采用枚举策略,当m=n时,共进行串比较:
Cn1*Cm1+Cn2*Cm2+Cn3*Cm3+……+Cnn*Cnn<22n 次,耗时太多,不可取。
此问题不可能简单地分解成几个独立的子问题,也不能用分治法来解。所以,我们只能用动态规划的方法去解决。
算法设计
1.递推关系分析
设 A=“a0,a1,…,am-1”, B=“b0,b1,…,bn-1”,
Z=“z0,z1,…,zk-1” 为它们的最长公共子序列。
有以下结论:
1)如果am-1=bn-1,则zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一个最长公共子序列;
2)如果am-1≠bn-1,则若zk-1≠am-1,蕴涵“z0,z1,…,zk-1”是"a0,a1,…,am-2"和"b0,b1,…,bn-1"的一个最长公共子 序列;
3)如果am-1≠bn-1,则若zk-1≠bn-1,蕴涵“z0,z1,…, zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列。
2.存储、子问题合并
定义c[i][j]为序列a0,a1,…,ai-2”和“b0,b1,…,bj-1”的
最长公共子序列的长度,计算c[i][j]可递归地表述如下:
1)c[i][j]=0 如果i=0或j=0;
2)c[i][j]=c[i-1][j-1]+1 如果i,j>0,且a[i-1]=b[j-1];
3)c[i][j]=max(c[i][j-1],c[i-1][j])
如果i,j>0,且a[i-1]≠b[j-1]。
算法(递归形式)
int Num=100
char a[Num],b[Num],str[Num];
main( )
{ int m,n,k;
print (“Enter two string”);
input(a,b);
m=strlen(a);
n=strlen(b),
k=lcs_len(n,m);
buile_lcs (k, n,m);
print(str);
}
lcs_len(int i,j) //计算最优值
{ if ( i=0 or j=0) c[i][j]=0;
else if (a[i-1]=b[j-1]) c[i][j]= lcs_len(i-1,j-1)+1 ;
else
{t1=lcs_len(i,j-1);
t2=lcs_len(i-1,j);
if (t1>t2)
c[i][j]=t1;
else
c[i][j]=t2;
}
return(c[i][j]);
}
buile_lcs (k,i,j); //构造最长公共子序列
{ if (i=0 or j=0 ) return;
if( c[i][j]=c[i-1][j] ) buile_lcs (k,i-1,j);
else if (c[i][j]=c[i][j-1] ) buile_lcs (k,i,j-1);
else { str[k]= a[i-1]; buile_lcs (k-1, i-1,j-1); }
}
算法(非递归)
n=100
char a[n],b[n],str[n];
lcs_len(char a[], char b[], int c[ ][ n]) //计算最优值
{ int m,n,i,j;
print (“Enter two string”); input(a,b);
m=strlen(a); n=strlen(b);
for (i=0;i<=m;i++) c[i][0]=0;
for (i=0;i<=n;i++) c[0][i]=0;
for (i=1;i<=m;i++)
for (j=1;j<=m;j++)
if (a[i-1]=b[j-1]) c[i][j]=c[i-1][j-1]+1;
else if (c[i-1][j]>=c[i][j-1]) c[i][j]=c[i-1][j];
else c[i][j]=c[i][j-1];
}
buile_lcs( ) //构造最长公共子序列
{ int k, i=strlen(a), j=strlen(b);
k=lcs_len( ); str[k]=’’;
while (k>0)
if (c[i][j]=c[i-1][j]) i=i-1;
else if (c[i][j]=c[i][j-1]) j=j-1;
else
{k=k-1;
str[k]=a[i-1];
j=j-1;}
}
【例5】最长不降子序列
设有由n个不相同的整数组成的数列,记为:
a(1)、a(2)、……、a(n)且a(i)<>a(j) (i<>j)
若存在i1<i2<i3< … <ik 且有a(i1)<a(i2)< … <a(ik),则称为长度为k的不下降序列。请求出一个数列的最长不下降序列
算法设计
1. 递推关系
1) 对a(n)来说,由于它是最后一个数,所以当从a(n)开始查找时,只存在长度为1的不下降序列;
2) 若从a(n-1)开始查找,则存在下面的两种可能性:
(1)若a(n-1)<a(n)则存在长度为2的不下降序列a(n-1),a(n)。
(2)若a(n-1)>a(n)则存在长度为1的不下降序列a(n-1)或a(n)。
3) 一般若从a(i)开始,此时最长不下降序列应该按下列方法求出:
在a(i+1),a(i+2),…,a(n)中,找出一个比a(i)大的且最长的不下降序列,作为它的后继。
2. 数据结构设计 用数组b[i], c[i]分别记录点i到n的最长的不降子序列的长度和点i后继接点的编号。
算法(逆推法)
int maxn=100;
int a[maxn],b[maxn],c[maxn];
main()
{ int n,i,j,max,p;
input(n);
for (i = 1;i <n;i++)
{ input(a[i]);
b[i]=1;
c[i]=0;
}
for (i=n-1; i>=1; i=i-1)
{max=0; p=0;
for(j=i+1; j<=n; j=j+1)
if (a[i]<a[j] and b[j]>max)
{max=b[j]; p=j;}
if( p<>0 ) { b[i]=b[p]+1; c[i]=p ;}
}
max=0; p=0;
for (i = 1;i <n;i++)
if (b[i]>max) { max:=b[i]; p:=i ; }
print('maxlong=',max); print ('result is:');
while (p<>0 )
{ print(a[p]); p:=c[p]; }
}



