9算法策略之分治法
分治算法
1.算法设计思想
分治法求解问题的过程是,将整个问题分解成若干个小问题后分而治之。如果分解得到的子问题相对来说还太大,则可反复使用分治策略将这些子问题分成更小的同类型子问题,直至产生出方便求解的子问题,必要时逐步合并这些子问题的解,从而得到问题的解。
分治法的基本步骤在每一层递归上都有三个步骤:
1)分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
2)解决:若子问题规模较小而容易被解决则直接解,否则再继续分解为更小的子问题,直到容易解决;
3)合并:将已求解的各个子问题的解,逐步合并为原问题的解。
有时问题分解后,不必求解所有的子问题,也就不必作第三步的操作。比如折半查找,在判别出问题的解在某一个子问题中后,其它的子问题就不必求解了,问题的解就是最后(最小)的子问题的解。分治法的这类应用,又称为“减治法”。
多数问题需要所有子问题的解,并由子问题的解,使用恰当的方法合并成为整个问题的解,比如合并排序,就是不断将子问题中已排好序的解合并成较大规模的有序子集。
2.适合用分治法策略的问题
当求解一个输入规模为n且取值又相当大的问题时,用蛮力策略效率一般得不到保证。若问题能满足以下几个条件,就能用分治法来提高解决问题的效率。
1) 能将这n个数据分解成k个不同子集合,且得到k个子集合是可以独立求解的子问题,其中1<k≤n;
2) 分解所得到的子问题与原问题具有相似的结构,便于利用递归或循环机制;
在求出这些子问题的解之后,就可以推解出原问题的解;
两个熟悉的例子
二分检索
算法2.1 BinarySearch(T, l, r, x)
输入:数组T,下标从 l 到 r;数 x
输出:j // 如果 x 在 T 中,j为下标;否则为0
1. l<-1; r<-n
2. while l<= r do
3. m<-[(l+r)/2]
4. if T[m]=x then return m // x恰好等于中位元素
5. else if T[m]>m then r<-m-1
6. else <-m+1
7. return 0
时间复杂度分析

分治算法的一般性描述

分治法的一般的算法设计模式如下:
Divide-and-Conquer(int n) /n为问题规模/
{ if (n≤n0) /n0 为可解子问题的规模/
{ 解子问题;
return(子问题的解);}
for (i=1
;i<=k;i++) /分解为较小子问题p1,p2,……pk/
yi=Divide-and-Conquer(|Pi|); /递归解决Pi/
T =MERGE(y1,y2,...,yk); /合并子问题/
return(T); }
其中|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。算法MERGE(y1,y2,...,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,...,Pk的相应的解y1,y2,...,yk合并为P的解。在一些问题中不需要这一步。如析半查找、4.3.2中的例1、例2等。
典型二分法
不同于现实中对问题(或工作)的分解,可能会考虑问题(或工作)的重点、难点、承担人员的能力等来进行问题的分解和分配。在算法设计中每次一个问题分解成的子问题个数一般是固定的,每个子问题的规模也是平均分配的。当每次都将问题分解为原问题规模的一半时,称为二分法。二分法是分治法较常用的分解策略,数据结构课程中的折半查找、归并排序等算法都是采用此策略实现的。
【例1】金块问题: 老板有一袋金块(共n块),最优秀的雇员得到其中最重的一块,最差的雇员得到其中最轻的一块。假设有一台比较重量的仪器,我们希望用最少的比较次数找出最重的金块。
算法设计1:比较简单的方法是逐个的进行比较查找。先拿两块比较重量,留下重的一个与下一块比较,直到全部比较完毕,就找到了最重的金子。算法类似于一趟选择排序,算法如下:
maxmin( float a[],int n)
{ max==min=a[1];
for(i=2 i<=n i++ )
if(max < a[i]) max=a[i];
else if(min > a[i]) min=a[i];
}
算法分析1:算法中需要n-1次比较得到max。最好的情况是金块是由小到大取出的,不需要进行与min的比较,共进行n-1次比较。最坏的情况是金块是由大到小取出的,需要再经过n-1次比较得到min,共进行2*n-2次比较。至于在平均情况下,A(i)将有一半的时间比max大,因此平均比较数是3(n—1)/2。
算法设计2:问题可以简化为:在含n(n是2的幂(n>=2))个元素的集合中寻找极大元和极小元。用分治法(二分法)可以用较少比较次数地解决上述问题:
1) 将数据等分为两组(两组数据可能差1),目的是分别选取其中的最大(小)值。
2) 递归分解直到每组元素的个数≤2,可简单地找到最大(小)值。
3) 回溯时将分解的两组解大者取大,小者取小,合并为当前问题的解。
算法2 递归求取最大和最小元素
float a[n];
maxmin (int i, int j ,float &fmax, float &fmin){int mid; float lmax, lmin, rmax, rmin;
if (i=j) {fmax= a[i]; fmin=a[i];}
else if (i=j-1)
if(a[i]<a[j]) { fmax=a[j];fmin=a[i];}
else {fmax=a[i]; fmin=a[j];}
else {mid=(i+j)/2;
maxmin (i,mid,lmax,lmin);
maxmin (mid+1,j,rmax,rmin);
if(lmax>rmax) fmax=lmax;
else fmax=rmax;
if(lmin>rmin) fmin=rmin;
else fmin=lmin;

二分法不相似情况
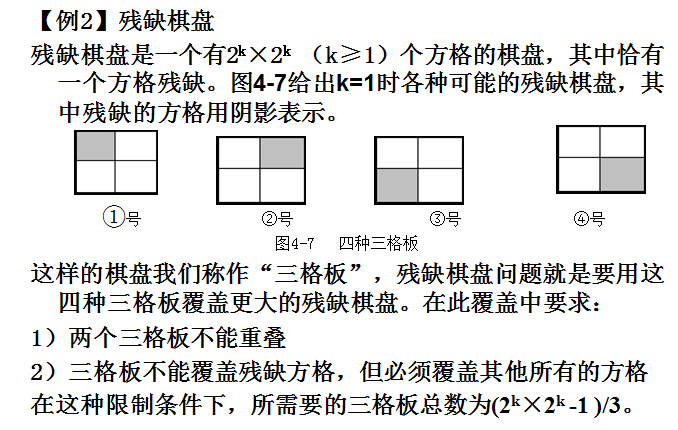
算法设计1:下面用分而治之方法解决残缺棋盘问题。
1)问题分解过程如下:
以k=2时的问题为例,用二分法进行分解,得到的是如下图4-8,用双线划分的四个k=1的棋盘。但要注意这四个棋盘,并不都是与原问题相似且独立的子问题。因为当如图4-8中的残缺方格在左上部时,第1个子问题与原问题相似,而右上角、左下角和右下角三个子棋盘(也就是图中标识为2、3、4号子棋盘),并不是原问题的相似子问题,自然也就不能独立求解了。当使用一个①号三格板(图中阴影)覆盖2、3、4号三个子棋盘的各一个方格后,如4-8右图所示,我们把覆盖后的方格,也看作是残缺方格(称为“伪”残缺方格),这时的2、3、4号子问题就是独立且与原问题相似的子问题了。

从以上例子还可以发现,当残缺方格在第1个子棋盘,用①号三格板覆盖其余三个子棋盘的交界方格,可以使另外三个子棋盘转化为独立子问题;同样地(如下图4-9所示),当残缺方格在第2个子棋盘时,则首先用②号三格板进行棋盘覆盖,当残缺方格在第3个子棋盘时,则首先用③号三格板进行棋盘覆盖,当残缺方格在第4个子棋盘时,则首先用④号三格板进行棋盘覆盖,这样就使另外三个子棋盘转化为独立子问题。如下图4-9:
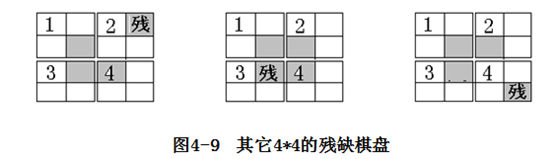
同样地k=1,2,3,4……都是如此,k=1为停止条件。
2)棋盘的识别
棋盘的规模是一个必要的信息,有了这个信息,只要知道其左上角的左上角方格所在行、列就可以唯一确定一个棋盘了,残缺方格或“伪”残缺方格直接用行、列号记录。
• tr 棋盘中左上角方格所在行。
• tc 棋盘中左上角方格所在列。
• dr 残缺方块所在行。
• dl 残缺方块所在列。
• size 棋盘的行数或列数。
数据结构设计:用二维数组board[ ][ ],模拟棋盘。覆盖残缺棋盘所需要的三格板数目为:( size2 -1 ) / 3将这些三格板编号为1到( s i z e2-1 ) / 3。则将残缺棋盘三格板编号的存储在数组board[ ][ ]的对应位置中,这样输出数组内容就是问题的解。结合图4-9,理解算法。
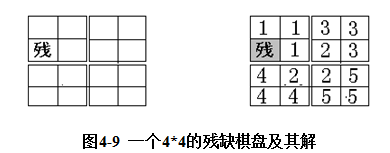
算法如下:
int amount=0;
main( )
{ int size=1,x,y;
input(k);
for (i=1;i<=k;i++) size=size*2;
print(“input incomplete pane ”);
input(x,y);
Cover(0, 0, x, y, size);
}
Cover(int tr, int tc, int dr, int dc, int size)
{ if (size<2) return;
int t = amount ++, // 所使用的三格板的数目
s=size/2; // 子问题棋盘大小
if (dr < tr + s && dc < tc + s) / /残缺方格位于左上棋盘
{Cover ( tr, tc, dr, dc, s);
Board[tr + s - 1][tc + s] = t; // 覆盖1号三格板
Board[tr + s][tc + s - 1] = t;
Board[tr + s][tc + s] = t;
Cover (tr, tc+s, tr+s-1, tc+s, s); // 覆盖其余部分
Cover(tr+s, tc, tr+s, tc+s-1, s);
Cover(tr+s, tc+s, tr+s, tc+s, s);
}
else if(dr < tr + s && dc >= tc + s) //残缺方格位于右上象限
{Cover ( t r, tc+s, dr, dc, s);
Board[tr + s - 1][tc + s - 1] = t; // 覆盖2号三格板
Board[tr + s][tc + s - 1] = t;
Board[tr + s][tc + s] = t;
Cover (tr, tc, tr+s-1, tc+s-1, s); //覆盖其余部分
Cover(tr+s, tc, tr+s, tc+s-1, s);
Cover(tr+s, tc+s, tr+s, tc+s, s);}
else if (dr >= tr + s && dc < tc + s) //残缺方格位于覆盖左下象限 { Cover(tr+s, tc, dr, dc, s);
Board[tr + s - 1][tc + s - 1] = t; // 覆盖3号三格板
Board[tr + s - 1][tc + s] = t;
Board[tr + s][tc + s] = t;
Cover (tr, tc, tr+s-1, tc+s-1, s); //覆盖其余部分
Cover (tr, tc+s, tr+s-1, tc+s, s);
Cover(tr+s, tc+s, tr+s, tc+s, s); }
else if (dr >= tr + s && dc >= tc + s) // 残缺方格位于右下象限
{Cover(tr+s, tc+s, dr, dc, s);
Board[tr + s - 1][tc + s - 1] = t; // 覆盖4号三格板
Board[tr + s - 1][tc + s] = t;
Board[tr + s][tc + s - 1] = t;
Cover (tr, tc, tr+s-1, tc+s-1, s); //覆盖其余部分
Cover (tr, tc+s, tr+s-1, tc+s, s);
Cover(tr+s, tc, tr+s, tc+s-1, s); }
}
void OutputBoard(int size)
{ for (int i = 0; i < size; i++)
{ for (int j = 0; j < size; j++)
print( Board[i][j]);
print(“换行符”); }
}
算法分析:因为要覆盖(size2 -1)/ 3个三格板,所以算法的时间复杂性为O(size2)。
二分法不独立情况
【例3】求数列的最大子段和
给定n个元素的整数列(可能为负整数)a1,a2 ,…,an。求形如:
ai,ai+1 ,…,aj i、j=1……n,i<=j的子段,使其和为最大。当所有整数均为负整数时定义其最大子段和为0。
例如当(a1,a2,a3,a4,a5,a6)=(-2,11,-4,13,-5,-2)时,最大子段和为i=2 ,j=4(下标从1开始)。
问题分析:若用二分法将实例中的数据分解为两组(-2,11,-4),(13,-5,-2),第一个子问题的解是11,第二个子问题的解是13,两个子问题的解不能简单地得到原问题的解。由此看出这个问题不能分解用二分法成解为独立的两个子问题,子问题中间还有公共的子问题,这类问题称为子问题重叠类的问题。那么,怎样解决这类问题呢?虽没有通用的方法,但本章4.5节的介绍的动态规划算法是一种较好的解决方法。下面我们仍用二分法解决这类问题中的一些简单问题,学习一下如何处理不独立的子问题。
算法设计:分解方法和上面的例题一样采用二分法,虽然分解后的子问题并不独立,但通过对重叠的子问题进行专门处理,并对所有子问题合并进行设计,就可以用二分策略解决此题。
如果将所给的序列a[1:n]分为长度相等的两段a[1:(n/2)]和a[(n/2)+1:n],分别求出这两段的最大子段和,则a[1:n]的最大子段和有3种情形。
情形(1)a[1:n]的最大子段和与a[1:(n/2)]的最大子段和相同;
情形 (2) a[1:n]的最大子段和与a[(n/2)+1:n]的最大子段和相同;
情形 (3) a[1:n]的最大子段和为a[i:j],且1≤i≤(n/2), (n/2)+1≤j≤n。
情况1)和情况2)可分别递归求得。
对于情况3),a[(n/2)]与a[(n/2)+1]一定在最优子序列中。因此,我们可以计算出a[i..(n/2)]的最大值s1;并计算出a[(n/2)+1..j]中的最大值s2。则s1+s2即为出现情况3)时的最优值。
算法如下:
int max_sum3(int a[ ],int n)
{return(max_sub_sum(a,1,n));}
max_sub_sum(int a[ ], int left, int right)
{int center,i,j,sum,left_sum,right_sum,s1,s2,lefts,rights;
if (left=right)
if (a[left]>0) return(a[left]) ;
else return(0);
else
{ center=(left+right)/2;
left_sum=max_sub_sum(a,left,center);
right_sum=max_sub_sum(a,center+1,right);
s1=0; /处理情形3/
lefts=0;
for (i=center;i>=left;i--)
{ lefts=lefts+a[i];
if( lefts>s1) s1=lefts;}
s2=0; rights=0;
for( i=center+1;i<= right;i++)
{ rights=rights+a[i];
if ( rights>s2) s2=rights;}
if (s1+s2<left_sum and right_sum<left_sum) rturn(left_sum);
if (s1+s2<right_sum) return(right_sum);
return(s1+s2);
}
}
【例4】大整数乘法
在某些情况下,我们需要处理很大的整数,它无法在计算机硬件能直接允许的范围内进行表示和处理。若用浮点数来存储它,只能近似地参与计算,计算结果的有效数字会受到限制。若要精确地表示大整数,并在计算结果中要求精确地得到所有位数上的数字,就必须用软件的方法来实现大整数的算术运算。请设计一个有效的算法,可以进行两个n位大整数的乘法运算。
数据结构设计:首先用数组存储大整数数据,再将两个乘数和积都按由低位到高位逐位存储到数组元素中。
算法设计1:存储好两个高精度数据后,模拟竖式乘法,让两个高精度数据的按位交叉相乘,并逐步累加即可得到精确的结果,用二重循环就可实现。
算法设计1:存储好两个高精度数据后,我们模拟竖式乘法,让两个高精度数据的按位交叉相乘,并逐步累加,即可得到精确的计算结果。用二重循环就可控制两个数不同位相乘的过程。
只考虑正整数的乘法,算法细节设计如下:
1) 对于大整数比较方便的输入方法是,按字符型处理,存储在字符串数组s1、s2中,计算结果存储在整型数组a中。
2)通过字符的ASCII码,数字字符可以直接参与运算,k位数字与j位数字相乘的表达式为:s1[k]-48)*(s2[j]-48)。这是C语言的处理方法,其它程序设计语言有对应的函可以实现数字字符与数字的转换,这里不详细介绍了。
3)每一次数字相乘的结果位数是不固定的,而结果数组中每个元素只存储一位数字,所以用变量b暂存结果,若超过1位数则进位,用变量d存储。这样每次计算的表达式为:
b= a[i]+(s1[k]-48)*(s2[j]-48)+d;。
算法如下:
main( )
{ long b,c,d; int i,i1,i2,j,k,n,n1,n2,a[256];
char s1[256],s2[256];
input(s1); input(s2);
for (i=0;i<255;i++) a[i]=0;
n1=strlen(s1); n2=strlen(s2); d=0;
for (i1=0,k=n1-1;i1<n1;i1++,k--)
{ for (i2=0,j=n2-1;i2<n2;i2++,j--)
{ i=i1+i2; b= a[i]+(s1[k]-48)*(s2[j]-48)+d;
a[i]= b mod 10; d=b/10;}
while (d>0)
{ i=i+1; a[i]= a[i]+d mod 10; d=d/10;}
n=i; }
for (i=n;i>=0;i--) print(a[i]);
}
算法说明:循环变量j、k分别是两个乘数字符串的下标。i1表示字符串str1由低位到高位的位数,范围0——n1-1(与k相同)。i2表示字符串str2由低位到高位的位数,范围0——n2-1(与j相同)。i表示乘法正在运算的位,也是计算结果存储的位置。
算法分析1:算法是以n1,n2代表两个乘数的位数,由算法中的循环嵌套知,算法的主要操作是乘法,算法的时间复杂度是O(n1*n2)。
算法设计2:下面们用分治法来设计一个更有效的大整数乘积算法。设计的重点是要提高乘法算法的效率,设计如下:
设X和Y都是n位的二进制整数,现在要计算它们的乘积X*Y。
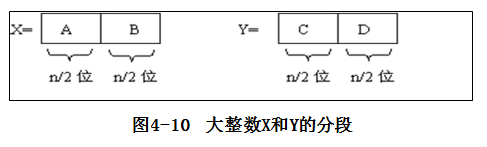
将n位的二进制整数X和Y各分为2段,每段的长为n/2位(为简单起见,假设n是2的幂),如图4-10所示。显然问题的答案并不是A*C*K1+C*D*K2(K1、K2与A、B、C、D无关),也就是说,这样做并没有将问题分解成两个独立的子问题。按照乘法分配律,分解后的计算过程如下:
记:X=A*2n/2+B ,Y=C*2n/2+D。这样,X和Y的乘积为:
X*Y=(A*2n/2+B)(C*2n/2+D)=A*C*2n+(AD+CB)*2n/2+B*D (1)
模型分析:
如果按式(1)计算X*Y,则我们必须进行4次n/2位整数的乘法(AC,AD,BC和BD),以及3次不超过n位的整数加法,此外还要做2次移位 (分别对应于式(1)中乘2n和乘2n/2)。所有这些加法和移位共用O(n)步运算。设T(n)是2个n位整数相乘所需的运算总数,则由式(1),我们有以下(2)式:
T(1)=1
T(n)=4T(n/2)+O(n) (2)
由此递归式迭代过程如下:
T(n)=4T(n/2)+cn =4(4T(n/4)+cn/2)+cn
=16(T(n/8)+ cn/4)+3cn/2+cn =……
=+4k-1 *2c+4k-2 *4c+……+4c2k-1+c2k
=O(4k)= O(nlog4)
=O(n2)
所以可得算法的时间复杂度为T(n)=O(n2)。
模型改进:
可以把X*Y写成另一种形式:
X*Y=A*C*2n+[(A-B)(D-C)+AC+BD]*2n/2+B*D (3)
式(3)看起来比式(1)复杂,但它仅需做3次n/2位整数的乘法:AC,BD和(A-B)(D-C),6次加、减法和2次移位。由此可得:
 (4)
(4)
用解递归方程的迭代公式法,不妨设n=2k:
T(n)=3T(n/2)+cn
=3(3T(n/4)+cn/2)+cn
=9(T(n/8)+ cn/4)+3cn/2+cn
=……
=3k +3k-1 *2c+3k-2 *4c+……+3c2k-1+c2k
= O(nlog3)
则得到T(n)=O(nlog3)=O(n1.59)。
MULT(X,Y,n) {X和Y为2个小于2n的整数,返回结果为X和Y的乘积XY}
{ S=SIGN(X)*SIGN(Y); //S为X和Y的符号乘积
X=ABS(X);
Y=ABS(Y); //X和Y分别取绝对值
if( n=1)
if (X=1 and Y=1) return(S);
else return(0);
else
{ A=X的左边n/2位;
B=X的右边n/2位;
C=Y的左边n/2位;
D=Y的右边n/2位;
ml=MULT(A,C,n/2);
m2=MULT(A-B,D-C,n/2);
m3=MULT(B,D,n/2);
S=S*(m1*2n+(m1+m2+m3)*2n/2+m3);
return(S); }
}
非等分分治
以上的例子都是用二分策略把问题分解为与原问题相似“相等”的子问题。下面看几个用“非等分二分法”解决问题的例子。
选择问题就是“从一组数中选择的第k小的数据”,这个问题的一个应用就是寻找中值元素,此时k = [n / 2 ]。中值是一个很有用的统计量,例如中间工资,中间年龄,中间重量等。k取其他值也是有意义的,例如,通过寻找第k=n/2 、k=n/3和 k=n/4的年龄,可将人口进行划分,了解人口的分布情况。
这个问题可以通过排序来解决,最好的排序算法的复杂性也是O(n*log(n)),下面我们要利用分治法,找到复杂性为O(n)的算法。但这个问题不能用简单的二分法分解成完全独立、相似的两个子问题。因为在选出分解后第一组的第k小的数据和第二组的第k小的数据,不能保证在这两个数据之一是原问题的解。
以求一组数的第二小的数据为例,我们讨论解决问题的办法。
【例5】选择问题1 求一组数的第二小的数。
float a[100];
main( )
{ int n; float min2;
input(n);
for (i=0;i<n-1;i=i+1) input(a[i]);
min2=second(n);
print(min2); }
second(int n)
{float min2,min1;
two(0,n-1, min2, min1);
return min2;}
two(int i, int j,float &fmin2, float &fmin1)
{ float lmin2,lmin1,rmin2,rmin1; int mid;
if (i=j) fmin2=fmin1=a[i]
else if (i=j-1)
if(a[i]<a[j]) { fmin2=a[j];fmin1=a[i];}
else {fmin2=a[i]; fmin1=a[j];}
else
{mid=(i+j)/2;
two(i,mid,lmin2,lmin1);
two(mid+1,j,rmin2,rmin1);
if (lmin1<rmin1)
if (lmin2<rmin1) { fmin1=lmin1;fmin2=lmin2;}
else {fmin1=lmin1; fmin2=rmin1;}
else
if ( rmin2<lmin1) { fmin1=rmin1;fmin2=rmin2;}
else {fmin1=rmin1; fmin2=lmin1;}
}}
算法分析:此算法的时间复杂度与【例1】相同,为O(n)。
以上算法利用“分解为与原问题相似的两个子问题”的技巧,较好地解决了一个简单的选择问题,但对于选取第k小元素的问题,若还用同样的技巧,在合并操作时还是需要进行排序,从效率上考虑就行不通了。同样,这个问题也不适合用上一小节介绍的处理公共子问题的方法来解决,因为二分治后的两个子问题的公共子问题是比较复杂的。
难道说这个问题就不适合用分治法来解决吗?至此为止,我们一直用二分法来解决问题,也就说总是将问题进行二等份分解,但分治法并不是只能有二分法一种表现形式,下面的例子,通过对数据整理,然后得到“非等份分解方法”的例子。
【例6】选择问题: 对于给定的n 个元素的数组a[0:n-1],要求从中找出第k小的元素。
问题分析:选择问题的一个应用就是寻找中值元素,此时k=[n/2]。
算法设计: 本题可以对全部数据进行排序后,找出问题的解。用较好的排序方法,算法的复杂性为O( n l o g n )。
可以通过改写快速排序算法来解决选择问题,一趟排序分解出的左子集中元素个数nleft,可能是以下几种情况:
1) nleft=k-1,则分界数据就是选择问题的答案。
2) nleft>k-1,则选择问题的答案继续在左子集中找,问题规模变小了。
3) nleft<k-1,则选择问题的答案继续在右子集中找,问题变为选择第k-nleft-1小的数,问题的规模也变小了。
xzwt(int a[ ], int n, int k ) //返回a [ 0 : n - 1 ]中第k小的元素
{ if (k < 1 || k > n) error( );
return select(a, 0, n-1, k); }
select(int a[ ], int left, int right, int k)
/在a [ left : right ]中选择第k小的元素/
{ if (left >= right) return a[left];
int i = left; //从左至右的指针
j = right + 1; // 从右到左的指针
int pivot = a[left]; //把最左面的元素作为分界数据
while (1)
do { // 在左侧寻找>= pivot 的元素
i = i + 1;
} while (a[i] < pivot);
do {j = j - 1; } while (a[j] > pivot); // 在右侧寻找<= pivot 的元素
if (i >= j) break; // 未发现交换对象
Swap(a[i], a[j]);
}
if (j - left + 1 = k) return pivot;
a[left] = a[j]; // 设置p i v o t
a[j] = pivot;
if (j - left + 1 < k) // 对一个段进行递归调用
return select(a, j+1, right, k-j -1+left);
else
return select(a, left, j-1, k);
}
算法分析:
1)以上算法在最坏情况下的复杂性是O( n2 ),此时left 总是为空,而且第k个元素总是位于 right子集中。
2)如果假定n是2的幂,通过迭代方法,可以得到算法的平均复杂性是O (n)。若仔细地选择分界元素,则最坏情况下的时间开销也可以变成(n)。一种选择分界元素的方法是使用“中间的中间(m e d i a n - o f - m e d i a n)”规则,该规则首先将数组a中的n 个元素分成n/r 组,r 为某一整常数,除了最后一组外,每组都有r 个元素。然后通过在每组中对r 个元素进行排序来寻找每组中位于中间位置的元素。最后根据所得到的n/r 个中间元素,递归使用选择算法,求得所需要的分界元素。这里不深入讨论。
3)注意到这个算法实质上只是利用了分治法的分解策略,分解后根据不同情况,只处理其中的一个子问题,并没有象【例1】一样有回溯合并的过程。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号