7算法策略之递推法
迭代算法
迭代法（Iteration）也称“辗转法”，是一种不断用变量的旧值递推出新值的解决问题的方法。迭代算法一般用于数值计算。迭代法应该是我们早已熟悉的算法策略，程序设计语言课程中所学的累加、累乘都是迭代算法策略的基础应用。
利用迭代算法策略求解问题，设计工作主要有三步：
1）确定迭代模型
2）建立迭代关系式
3）对迭代过程进行控制
递推法
【例1】兔子繁殖问题
问题描述：一对兔子从出生后第三个月开始，每月生一对小兔子。小兔子到第三个月又开始生下一代小兔子。假若兔子只生不死，一月份抱来一对刚出生的小兔子，问一年中每个月各有多少对兔子。
问题分析：因一对兔子从出生后第三个月开始每月生一对小兔子，则每月新下小兔子的对儿数(用斜体数字表示)显然由前两个月的小兔子的对儿数决定。则繁殖过程如下：
一月 二月 三月 四月 五月 六月 ……
1 1 1+1=2 2+1=3 3+2=5 5+3=8 ……
算法1：
main( )
{ int i,a=1,b=1;
print(a,b);
for(i=1;i＜=10;i++)
{ c=a+b;
print (c);
a=b;
b=c；
}
}
算法2：
表4-1 递推迭代表达式
1 2 3 4 5 6 7 8 9
a b c=a+b a=b+c b=a+c c=a+b a=b+c b=a+c ……
由此归纳出可以用“c=a+b; a=b+c; b=c+a;”做循环“不变式”。
算法2如下：
main( )
{ int i,a=1,b=1;
print(a,b);
for(i=1; i＜=4;i++)
{ c=a+b; a=b+c; b=c+a; print(a,b,c); }
}
算法2，最后输出的并不是12项，而是2+3*4共14项。
算法3：
表4-2 递推迭代表达式
1 2 3 4 5 6 7 8 9
a b a=a+b b=a+b a=a+b b=a+b ……
由此归纳出可以用“a=a+b; b=a+b;”做循环“不变式”，从而得到以下算法3:
main( )
{ int i,a=1,b=1;
print(a,b);
for(i=1; i＜=5;i++)
{ a=a+b; b=a+b; print(a,b); }
}
【例2】求两个整数的最大公约数。
数学建模：辗转相除法是根据递推策略设计的。
不妨设两个整数a>b且a除以b商x余c；则a-bx=c，不难看出a、b的最大公约数也是c的约数（一个数能整除等式左边就一定能整除等式的右边），则a、b的最大公约数与b、c的最大公约数相同。同样方法推出b、c的最大公约数与……，直到余数为0时，除数即为所求的最大公约数。
算法设计：循环“不变式”第一次是求a、b相除的余数c，第二次还是求“a”“b” 相除的余数，经a=b,b=c操作，就实现了第二次还是求“a”“b” 相除的余数，这就找到了循环不变式。循环在余数c为0时结束。
算法如下：
main（）
{ int a, b;
input(a,b);
if(b=0)
{print(“data error”);
return;}
else
{ c = a mod b;
while c<>0
{ a=b;
b=c;
c=a mod b;}
}
print(b);
}
倒推法
所谓倒推法：是对某些特殊问题所采用的违反通常习惯的，从 后向前推解问题的方法。如下面的例题，因不同方面的需求而采用了倒推策略。
例1在不知前提条件的情况下，经过从后向前递推，从而求解问题。即由结果倒过来推解它的前提条件。又如例2由于存储的要求，而必须从后向前进行推算。另外，在对一些问题进行分析或建立数学模型时，从前向后分析问题感到比较棘手，而采用倒推法（如例3），则问题容易理解和解决。下面分别看这几个例子：
【例1】猴子吃桃问题
一只小猴子摘了若干桃子，每天吃现有桃的一半多一个，
到第10天时就只有一个桃子了，求原有多少个桃？
数学模型：每天的桃子数为：a10=1, a9=(1+a10)*2, a8=(1+a9)*2,……a10=1，
递推公式为：ai=(1+ai+1)*2 I = 9,8,7,6……1
算法如下 ：
main( )
{ int i,s;
s=1;
for (i=9 ;i>=1;i=i-1)
s=(s+1)*2
print (s)；
}
【例2】 输出如图4-1的杨辉三角形（限定用一个一维数组完成）。
数学模型：上下层规律较明显，中间的数等于上行左上、右上两数之和。
问题分析：题目中要求用一个一维数组即完成。数组空间一定是由下标从小到大利用的，这样其实杨辉三角形是按下图4-2形式存储的。若求n层，则数组最多存储n个数据。
算法设计：
A[1] = A[i]=1
A[j] = A[j] + A[j-1] j=i-1，i-2，……，2
i行 i-1行 i-1行
算法如下：
main( )
{int n,i,j,a[100];
input(n);
print(“1”); print(“换行符”);
a[1]=a[2]=1;
print(a[1],a[2]); print(“换行符”);
for (i=3;i<=n;i=i+1)
{a[1]=a[i]=1;
for (j=i-1，j>1，j=j-1)
a[j]=a[j]+a[j-1];
for (j=1;j<=i;j=j+1) print(a[j]);
print(“换行符”);
}
}
【例3】穿越沙漠问题
用一辆吉普车穿越1000公里的沙漠。吉普车的总装油量为500加仑，耗油率为1加仑/公里。由于沙漠中没有油库，必须先用这辆车在沙漠中建立临时油库。该吉普车以最少的耗油量穿越沙漠，应在什么地方建油库，以及各处的贮油量。
问题分析：
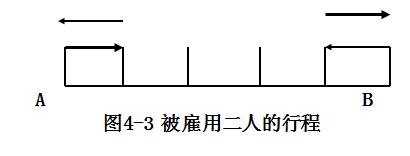
1）先看一简单问题：有一位探险家用5天的时间徒步横穿A、B两村，两村间是荒无人烟的沙漠，如果一个人只能担负3天的食物和水，那么这个探险家至少雇几个人才能顺利通过沙漠。
A城雇用一人与探险家同带3天食物同行一天，然后被雇人带一天食物返回，并留一天食物给探险家，这样探险家正好有3天的食物继续前行，并于第三天打电话雇B城人带3天食物出发，第四天会面他们会面，探险家得到一天的食物赴B城。如图4-3主要表示了被雇用二人的行程。
2）贮油点问题要求要以最少的耗油量穿越沙漠，即到达终点时，沙漠中的各临时油库和车的装油量均为0。这样只能从终点开始向前倒着推解贮油点和贮油量。
数学模型：根据耗油量最少目标的分析，下面从后向前分段讨论。
第一段长度为500公里且第一个加油点贮油为500加仑。
第二段中为了贮备油，吉普车在这段的行程必须有往返。下面讨论怎样走效率高：
1）首先不计方向这段应走奇数次（保证最后向前走）。
2）每次向前行进时吉普车是满载。
3）要能贮存够下一加油点的贮油量，路上耗油又最少。
……
下图是满足以上条件的最佳方案，此段共走3次：第一、二次来回耗油2/3贮油1/3，第三次耗油1/3贮油2/3，所以第二个加油点贮油为1000加仑。由于每公里耗油率为1加仑，则此段长度为500/3公里。
第三段与第二段思路相同。下图是一最佳方案此段共走5次：第一、二次来回耗油2/5贮油3/5，第三、四次来回耗油2/5贮油3/5，第五次耗油1/5贮油4/5，第三个加油点贮油为1500加仑。此段长度为500/5。 ……
500/5公里
<———
500/3公里 ———>
<——— <———
500公里 第一 ———> 第二 ———> 第三
终点<——贮油点（500）<——贮油点（1000）<———贮油点（1500）……
图4-4 贮油点及贮油量示意
综上分析，从终点开始分别间隔 500，500/3，500/5，500/7，……（公里）设立贮油点，直到总距离超过1000公里。每个贮油点的油量为500，1000，1500，……。
算法设计：由模型知道此问题并不必用倒推算法解决（只是分析过程用的是倒推法），只需通过累加算法就能解决。变量说明：dis表示距终点的距离，1000- dis则表示距起点的距离，k表示贮油点从后到前的序号。
desert（ ）
{ int dis，k，oil,k;
dis=500;k=1;oil=500;
do{
print(“storepoint”,k,”distance”,1000-dis,”oilquantity”,oil)；
k=k+1;
dis=dis+500/(2*k-1);
oil= 500*k;
}while ( dis<1000)
oil=500*(k-1)+(1000-dis)*( 2*k-1); print(“storepoint”,k,”distance”,0,”oilquantity”,oil)；
}
迭代法解方程
迭代法解方程的实质是按照下列步骤构造一个序列x0,x1,…,xn,来逐步逼近方程f(x)=0的解：
1）选取适当的初值x0；
2）确定迭代格式，即建立迭代关系，需要将方程f(x)=0改写为x=φ(x)的等价形式； a构造序列x0，x1，……，xn，即先求得x1=φ(x0)，再求x2=φ(x1)，……如此反复迭代，就得到一个数列x0，x1，……，xn，若这个数列收敛，即存在极值，且函数φ(x)连续，则很容易得到这个极限值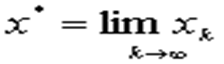
，x*就是方程f(x)=0的根。
【例1】迭代法求方程组根
算法说明：方程组解的初值X=（x0，x1，…，xn-1）,迭代关系方程组为：xi=gi(X)(i=0,1,…,n-1),w为解的精度,则算法如下：
for (i=0;i<n;i++)
x[i]=初始近似根;
do { k=k+1;
for (i=0;i<n;i y[i]=x[i];
for (i=0;i<n;i++) x[i]=gi(X);
for (i=0;i<n;i++) c=c+fabs(y[i]-x[i])；
} while (c>w and k<maxn )；
for (i=0;i<n;i++)
print(i，“变量的近似根是”，x[i])；
}
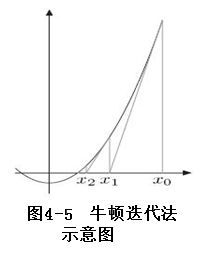
【例2】牛顿迭代法
牛顿迭代法又称为切线法，它比一般的迭代法有更高的收敛速度，如图4-5所示。首先, 选择一个接近函数f(x)零点的x0, 计算相应的f(x0)和切线斜率f‘(x0)（这里f ’表示函数f的导数）。然后我们计算穿过点(x0,f (x0))且斜率为f ‘(x0)的直线方程为：
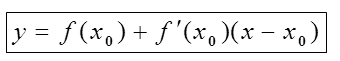
和x轴的交点的x坐标, 也就是求如下方程的解
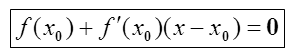
将新求得交点的x坐标命名为x1。如图4-5所示，通常x1会比x0更接近方程f(x) = 0的解。接下来用x1开始下一轮迭代 .
迭代公式可化简为：
此公式就是有名的牛顿迭代公式。已经证明, 如果f‘是连续的, 并且待求的零点x是孤立的, 那么在零点x周围存在一个区域, 只要初始值x0位于这个邻近区域内, 那么牛顿
法必定收敛。
下面给出用牛顿迭代法，求形如ax3+bx2+cx+d=0方程根的算法，系数a、b、c、d的值依次为1、2、3、4，由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。
main( )
{ float a , b, c, d, fx;
print("输入系数 a,b,c,d:");
input(a,b,c,d);
fx=f(a,b,c,d);
printf("方程的根为：",fx);
}
float f(a,b,c,d)
{
float a,b,c,d;
float x1=1 , x0, f0 , f1;
do
{ x0=x1;
f0=((a*x0+b)*x0+c)*x0+d;
f1=(3*a*x0+2*b)*x0+c;
x1=x0-f0/f1;
} while(fabs(x1-x0)>=1e-4);
return(x1);
}
【例3】二分法求解方程f(x)=0根 用二分法求解方程f(x)=0根的前提条件是：f(x)在求解的区间[a,b]上是连续的，且已知f(a)与f(b)异号，即 f(a)*f(b)<0。
令[a0,b0]=[a,b]，c0=(a0+b0)/2，若f(c0)=0，则c0为方程f(x)=0的根；否则，若f(a0)与f(c0)异号，即 f(a0)*f(c0)<0，则令[a1,b1]=[a0,c0]；若f(b0)与f(c0)异号，即 f(b0)*f(c0)<0，则令[a1,b1]=[c0,b0]。
依此做下去，当发现f(cn)=0时，或区间[an,bn]足够小，比如| an-bn |<0.0001时，就认为找到了方程的根。
用二分法求一元非线性方程f(x)= x^3/2+2x^2-8=0（其中^表示幂运算）在区间[0，2]上的近似实根r，精确到0.0001.算法如下：
main( )
{ float x,x1=0,x2=2,f1,f2,f;
print(“input a,b (f(a)*f(b)<0)”); input(a,b);
f1=x1*x1*x1/2+2*x1*x1-8; f2=x2*x2*x2/2+2*x2*x2-8;
if(f1*f2>0) { printf("No root"); return;}
do
{ x=(x1+x2)/2;
f=x*x*x/2+2*x*x-8;
if(f=0) break;
if(f1*f>0.0) {x1=x; f1=x1*x1*x1/2+2*x1*x1-8;}
else x2=x;
}while(fabs(f)>=1e-4);
print("root=",x);
}
设计算法求1-100中的数据i,i满足i,i+2.i+4,i+10均为素数
int prime( int n)
{int i;
for (i=2;i<=n-1;i++)
if（n%i==0）return 0;
return 1;
}
main( )
{int i;
for (i=1;i<=100;i++)
if（prime(i)&& prime(i+2)&& prime(i+4)&& prime(i+10)）
print(i);
}
