多维尺度变换MDS(Multidimensional Scaling)

流形学习（Manifold Learning）是机器学习中一大类算法的统称，流形学习是非线性的降维方法（an approach to non-linear dimensionality reduction）。PCA、LDA等降维方法基于线性假设，经常会损失数据内部非线性的结构信息；流形学习是线性降维方法的generalization，目的是捕获数据内部非线性的结构。而MDS就是流行学习中非常经典的一种方法。

 

多维尺度变换是一种在低维空间展示“距离”数据结构的多元数据分析技术,是一种将多维空间的研究对象简化到低维空间进行定位、分析和归类，同时又保留对象间原始关系的数据分析方法。多维尺度变换算法集中于保留高维空间中的“相似度”信息，而在一般的问题解决的过程中，这个“相似度”通常用欧式距离来定义。

通俗来讲，就是将多维数据映射到低维空间，同时保持各个样本之间的原有相对距离不变。

 

多维尺度变换的目标：当n 个对象中各对对象之间的相似性（或距离）给定时，确定这些对象在低维(欧式) 空间中的表示（称为感知图, Perceptual Mapping），
并使其尽可能与原先的相似性（或距离）“大体匹配”，使得由降维所引起的任何变形达到最小。

多维尺度变换可以应用到数据可视化，通过可视化找出异常点，反欺诈应用等。

 

计算步骤大致如下：

第一步：计算所有数据项两两间的实际距离（可参考皮尔逊算法或欧几里德算法）

第二步：将数据项随机放置在二维图上。

第三步：针对每两两构成的一对数据项，将它们的实际距离与当前在二维图上的距离进行比较，求出一个误差值

第四步：根据误差的情况，按照比例将每个数据项的所在位置移近或移远少许量。（每一个节点的移动，都是所有其它节点施加在该节点上的推或拉的结合效应。）

第五步：重复第三步、第四步（节点每移动一次，其当前距离与实际距离的差距就会减少一些）。这一过程会不断地重复多次，直到无法再通过移动节点来减少总体误差为止。

 

python 实现

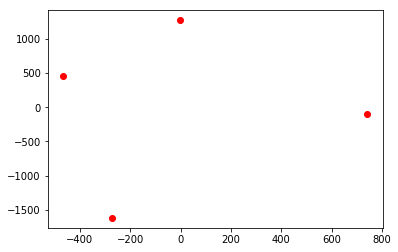
已知四个城市之间的距离，如何展示出他们的相对位置，原理就是利用MDS将多维数据映射到二维空间，作为经纬度坐标，同时之间的相对距离保持不变。

import numpy as np
import pandas as pd
from sklearn.manifold import MDS
import matplotlib.pyplot as plt
#%%
data = np.array([(0,1046,608,1859),
                 (1046,0,825,1149),
                 (608,825,0,1280),
                 (1859,1149,1280,0)
                ]
               )
index = ['beijing','shanghai','zhengzhou','guangzhou']
columns = ['beijing','shanghai','zhengzhou','guangzhou']
Word = pd.DataFrame(data,index,columns)
Word
#%%
mds = MDS()
mds.fit(data)
#%%
a = mds.embedding_
print(a)
plt.scatter(a[0:,0],a[0:,1],color='red')