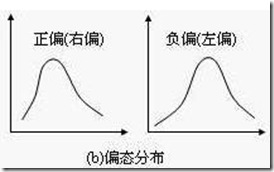
数据的偏态分布

一、何为数据的偏态分布？

 

频数分布有正态分布和偏态分布之分。正态分布是指多数频数集中在中央位置，两端的频数分布大致对称。

 

偏态分布是指频数分布不对称，集中位置偏向一侧。若集中位置偏向数值小的一侧，称为正偏态分布；集中位置偏向数值大的一侧，称为负偏态分布。

 

如果频数分布的高峰向左偏移，长尾向右侧延伸称为正偏态分布，也称右偏态分布；同样的，如果频数分布的高峰向右偏移，长尾向左延伸则成为负偏态分布，也称左偏态分布。

 

峰左移，右偏，正偏

 

峰右移，左偏，负偏

 

 性质：

1、当总体分布呈对称状态时，中位数=平均数

2、当总体分布呈右偏态状态时，说明存在极大值，会把平均值向极大值方向拉，中位数<平均数

3、当总体分布呈左偏态状态时，说明存在极小值，会把平均值向极小值方向拉，中位数>平均数

 

偏态分布只有满足一定的条件（如样本例数够大等）才可以看做近似正态分布。

 

与正态分布相对而言，偏态分布有两个特点：

 

　　一是左右不对称（即所谓偏态）；

 

　　二是当样本增大时，其均数趋向正态分布。

 

二、构建模型时为什么要尽量将偏态数据转换为正态分布数据？

　　数据整体服从正态分布，那样本均值和方差则相互独立。正态分布具有很多好的性质，很多模型假设数据服从正态分布。例如线性回归(linear regression)，它假设误差服从正态分布，从而每个样本点出现的概率就可以表示成正态分布的形式，将多个样本点连乘再取对数，就是所有训练集样本出现的条件概率，最大化这个条件概率就是LR要最终求解的问题。这里这个条件概率的最终表达式的形式就是我们熟悉的误差平方和。总之， ML中很多model都假设数据或参数服从正态分布。