python实现排序算法
一、冒泡排序
#完整的冒泡排序
def bubbleSort(arr): for i in range(len(arr)):#控制轮次 for j in range(len(arr)-1-i): #真正进行比较,数大的一层层下沉 change=False #比较前设置为False if arr[j]>arr[j+1]: arr[j],arr[j+1]=arr[j+1],arr[j] change=True if change==False:#一轮下来,只要发现没有交换了,说明已经有序了,就返回,尽量节省比较次数 return arr return arr a=[100,1,2,3,4,5,7] print(bubbleSort(a))
二、快速排序
def quicksort(arr): if len(arr) <= 1: return arr pivot = arr[len(arr) / 2] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quicksort(left) + middle + quicksort(right)
一个函数搞定的简洁版本
def quickSort(arr,start, end): if start>=end: return small,p=start,start+1 #这里的start就相当于pivot,找到他的正确位置 while p<=end: if arr[p]<=arr[start]: small+=1 arr[small],arr[p]=arr[p],arr[small] p+=1 arr[start],arr[small]=arr[small],arr[start] #最后交换过来,确保small左边的都小于small,右边的都大于small。 quickSort(arr,start,small-1) quickSort(arr,small+1,end) a=[9,0,1,10,8,2] quickSort(a,0,len(a)-1) print(a)
非递归实现
def quickSort(arr): left=0 right=len(arr)-1 s=[] s.append(left) s.append(right) while len(s)>0: left=s.pop(0) right=s.pop(0) k=partition(arr,left,right) if left<k-1: s.append(left) s.append(k-1) if right>k+1: s.append(k+1) s.append(right) #一次分割
def partition(data,start,end):
if len(data)==1:
return 0
small=start
p=small+1
while p<=end:
if data[p]<data[start]:
small+=1
data[p],data[small]=data[small],data[p]
p+=1
data[start],data[small]=data[small],data[start]
return small
单链表快速排序
void quicksort(Linklist head, Linklist end){ 2. if(head == NULL || head == end) //如果头指针为空或者链表为空,直接返回 3. return ; 4. int t; 5. Linklist p = head -> next; //用来遍历的指针 6. Linklist small = head; 7. while( p != end){ 8. if( p -> data < head -> data){ //对于小于轴的元素放在左边 9. small = small -> next; 10. t = small -> data; 11. small -> data = p -> data; 12. p -> data = t; 13. } 14. p = p -> next; 15. } 16. t = head -> data; //遍历完后,对左轴元素与small指向的元素交换 17. head -> data = small -> data; 18. small -> data = t; 19. quicksort(head, small); //对左右进行递归 20. quicksort(small -> next, end); 21.}
三、堆排序
递归简化版本
def heapSort(data,start,end): if start==end: return for i in range((end-1)//2,-1,-1): #数组最后一个元素下标除以2就是其负节点的下标,这里就是先找到第一个父节点,之后-1不断遍历其它父节点 root=i left=2*root+1 right=left+1 if left<=end and data[left]>data[root]: data[root],data[left]=data[left],data[root] if right<=end and data[right]>data[root]: data[root],data[right]=data[right],data[root] data[0],data[end]=data[end],data[0] #遍历完最大的元素就在data[0]里了,这个时候放到数组尾部即可。 heapSort(data,start,end-1) #接下来对剩余的元素继续堆排序。 return data a = [8,0,0,1,9] res=heapSort(a,0,len(a)-1) print(res)
最早版本,由于写法过于冗余,不如上面干净利落,可以舍弃。
def MAX_Heapify(heap,end): HeapSize = len(heap)-end for i in range((HeapSize-2)//2,-1,-1):
#(每个叶子节点的数组坐标-1)/2都等于其父节点的数组下标,这里面heapsize-2是先-1变成数组下标,然后再-1才能除以2找第一个父节点 root=i left = 2 * root + 1 right = left + 1 if left < HeapSize and heap[root] < heap[left]: heap[root],heap[left]=heap[left],heap[root] if right < HeapSize and heap[root] < heap[right]: heap[root], heap[right] = heap[right], heap[root] return heap def HeapSort(heap): length=len(heap) for i in range(length): MAX_Heapify(heap,i)#调整大根堆 heap[0],heap[length-1-i]=heap[length-1-i],heap[0] #将最大元素放到数组最后 return heap if __name__ == '__main__': a = [0,49,38,65,97,76,13,27,49] print(HeapSort(a))
注:大根堆得到的排序是升序,小根堆得到的排序是升序。
四、归并排序
合并成一个函数的版本
def mergeSort(data,start,end): if start==end: #相等的时候就代表这个时候只有一个元素了。 return mid=(start+end)//2 mergeSort(data,start,mid) mergeSort(data,mid+1,end) p1,p2=start,mid+1 tmp=[] #开始有序归并 while p1<=mid and p2<=end: if data[p1]<data[p2]: tmp.append(data[p1]) p1+=1 else: tmp.append(data[p2]) p2+=1 while p1<=mid: tmp.append(data[p1]) p1+=1 while p2<=end: tmp.append(data[p2]) p2+=1 data[start:end+1]=tmp return a=[90,0,0,0,1,1,8] mergeSort(a,0,len(a)-1) a
最早两个函数的版本
#归并排序 def mergeSort(data,start,end): if len(data)==0 or start>=end: return mid=(start+end)//2 mergeSort(data,start,mid) mergeSort(data,mid+1,end) merge(data,start,mid,end) def merge(data,start,mid,end): tmp=[] i=start j=mid+1 while i<=mid and j<=end: if data[i]<data[j]: tmp.append(data[i]) i+=1 else: tmp.append(data[j]) j+=1 while i<=mid: tmp.append(data[i]) i += 1 while j<=end: tmp.append(data[j]) j += 1 #排序后的添加到相应的位置中
data[start:end+1]=tmp
return
a=[2,4,1,7,6,5]
mergeSort(a,0,len(a)-1) print(a)
五、排序算法的稳定性
通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下,如果Ai = Aj, Ai原来在位置前,排序后Ai还是要在Aj位置前。
稳定性的意义
1、如果只是简单的进行数字的排序,那么稳定性将毫无意义。
2、如果排序的内容仅仅是一个复杂对象的某一个数字属性,那么稳定性依旧将毫无意义(所谓的交换操作的开销已经算在算法的开销内了,如果嫌弃这种开销,不如换算法好了?)
3、如果要排序的内容是一个复杂对象的多个数字属性,但是其原本的初始顺序毫无意义,那么稳定性依旧将毫无意义。
4、除非要排序的内容是一个复杂对象的多个数字属性,且其原本的初始顺序存在意义,那么我们需要在二次排序的基础上保持原有排序的意义,才需要使用到稳定性的算法,例如要排序的内容是一组原本按照价格高低排序的对象,如今需要按照销量高低排序,使用稳定性算法,可以使得想同销量的对象依旧保持着价格高低的排序展现,只有销量不同的才会重新排序。(当然,如果需求不需要保持初始的排序意义,那么使用稳定性算法依旧将毫无意义)
总结:
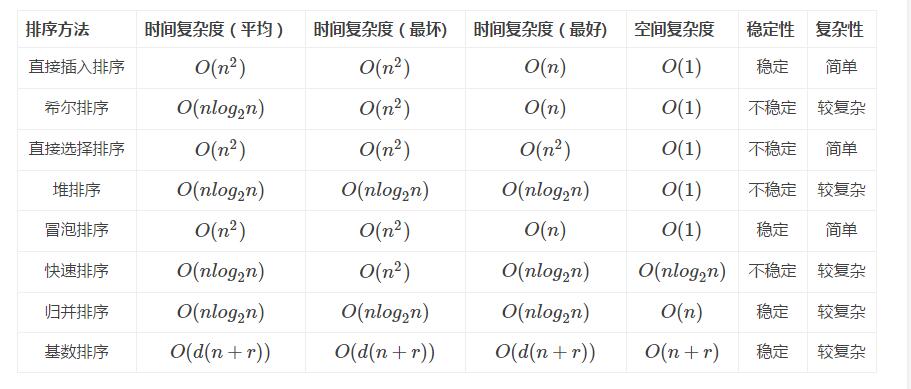
若从空间复杂度来考虑:首选堆排序,其次是快速排序,最后是归并排序。
若从稳定性来考虑,应选取归并排序,因为堆排序和快速排序都是不稳定的。
若从平均情况下的排序速度考虑,应该选择快速排序。



